Introduction
This is a light-hearted little piece of code I wrote to help deal with questions like "Are we nearly there yet?" of young children when driving a car.
Here is the idea. My daughter is in second class and has learnt to count, but it takes time for children to appreciate numbers and magnitudes. This is an important part of "Computational Thinking"; there is a sort of progression when children learn how to count and work with numbers. Based on my observation (and that is based on a sample of 2 or so), counting starts with very concrete objects like pieces of chocolate or building bricks or so. Only later will children learn to appreciate numbers as more abstract entities. It is typical that little children struggle to understand the magnitude of a number - they might be quite poor at estimating ages of people for a long time and putting numbers in perspective. ("How come that 1000$ is a lot, but 1000 grains of sand is too little to play with?")
If I answer the question "Are we nearly there yet?" with "30 minutes from now." It doesn't necessarily mean much. Saying "one episode of your favourite program" appears to be a more meaningful answer.
Now, we came up with this concept, where I basically tell my daughter to count to a certain number: Clara: "How long until my food is ready?" Me:"Count to 150."
Now I could do this very simply. There are all these calculations like: "To what number could I count if I were counting at a rate of one number per second and were to count all my life?"

gives 72.6yr, which I can then UnitConvert to seconds:
UnitConvert[Quantity[72.6, "Years"], "Seconds"]
That gives about 2.29 * 10^ 9 seconds and that would be what a person could count to if they start counting when they are born, and never sleep or do anything else, and get to say one number per second. Some of these assumptions might not be realistic.
Coding actual counting
I was interested in the actual counting time, i.e. ignoring sleep, breaks etc, and just wondering how many numbers I could really say in a given time, if I didn't do anything else. So I could ask Mathematica to make a sound file and speaking numbers for me. Counting up to 10 (at a reasonable speed) would look like this:
SpeechSynthesize[StringRiffle[StringReplace[IntegerName[#], "\[Hyphen]" -> " "] & /@ Range[10],
", "]]
Using Duration, I can find out how long it takes to say this:
Duration[SpeechSynthesize[StringRiffle[StringReplace[IntegerName[#], "\[Hyphen]" -> " "] & /@ Range[10], ", "]]]
I obtain 6.45732 s, which is too high a precision for my taste, but gives me an idea of how long it takes to count up to 10. So it takes an average of 0.645732 seconds to say one of the numbers. As numbers become larger, it will take longer to say them. Let's count up to 100:
Duration[SpeechSynthesize[StringRiffle[StringReplace[IntegerName[#], "\[Hyphen]" -> " "] & /@ Range[100], ", "]]]
which gives me 1min 44.4055 seconds, which is about 1.046 seconds per number. Counting up to 1000 is still an easy thing to do:
Duration[SpeechSynthesize[StringRiffle[StringReplace[IntegerName[#], "\[Hyphen]" -> " "] & /@ Range[1000],", "]]]
gives 27 min 50.0569 seconds, which is on average 1.67007 seconds per number. Now I could produce longer and longer sound files, but if I count up to larger numbers that is not the most practical thing to do. So lets do a random sampling approach. If we want to estimate how long it takes to count to one million, I could ask Mathematica to choose 100 numbers and then scale up to 1.000.000:
1000000/100*Duration[SpeechSynthesize[StringRiffle[StringReplace[IntegerName[#], "\[Hyphen]" -> " "] & /@ RandomSample[Range[1000000], 100], ", "]]]
Every time you run this you get slightly different results. Here are the results from 10 "realisations":

Of course, I can get better estimates by sampling more than 100 numbers. I would also like to use mixed units so give a better idea of the times. Here is a simple piece of code to do this:
Monitor[
results = Table[{k, UnitConvert[k/1000*Duration[SpeechSynthesize[
StringRiffle[StringReplace[IntegerName[#], "\[Hyphen]" -> " "] & /@
RandomSample[Range[k], 1000], ", "]]],
MixedUnit[{"Years", "Months", "Days", "Hours", "Minutes",
"Seconds"}]]}, {k, NestList[10*# &, 1000, 6]}], k]
Not the most elegant piece of code, but it gets the job done:

Other languages
Of course, we can try this in different languages:
Monitor[resultsgerman =
Table[{k, UnitConvert[k/1000*Duration[SpeechSynthesize[
StringRiffle[IntegerName[#, Language -> "German"] & /@
RandomSample[Range[k], 1000], ", "], Language -> "German"]],
MixedUnit[{"Years", "Months", "Days", "Hours", "Minutes",
"Seconds"}]]}, {k, NestList[10*# &, 1000, 6]}], k]
which gives:

So it appears that Germans count a bit more slowly than English native speakers. Let's have a look at Spanish:
Monitor[resultsspanish =
Table[{k, UnitConvert[k/1000*Duration[SpeechSynthesize[
StringRiffle[IntegerName[#, Language -> "Spanish"] & /@
RandomSample[Range[k], 1000], ", "], Language -> "Spanish"]],
MixedUnit[{"Years", "Months", "Days", "Hours", "Minutes",
"Seconds"}]]}, {k, NestList[10*# &, 1000, 6]}], k]
which gives:

I tried some other languages, too, but that doesn't contribute a lot to this parenting problem.
Higher resolution
For the next application, I want some higher resolution data for English.
Monitor[resultsEnglishHighRes =
Table[{k, UnitConvert[k/Min[1000, k]*
Duration[SpeechSynthesize[StringRiffle[StringReplace[IntegerName[#], "\[Hyphen]" -> " "] & /@
RandomSample[Range[k], Min[1000, k]], ", "]]],
MixedUnit[{"Years", "Months", "Days", "Hours", "Minutes",
"Seconds"}]]}, {k, Floor /@ Table[10^k, {k, 1, 9, 1/10}]}], k]
This gives me a long table; I'll only show every second entry though:

That's some serious counting going on right here.... If we plot this, we get:
ListLogLogPlot[{#[[1]], QuantityMagnitude[UnitConvert[#[[2]], "Seconds"]]} & /@
resultsEnglishHighRes, PlotRange -> All, LabelStyle -> Directive[Bold, Medium],
AxesLabel -> {"Count to", "Time in seconds"}, PlotStyle -> Red]
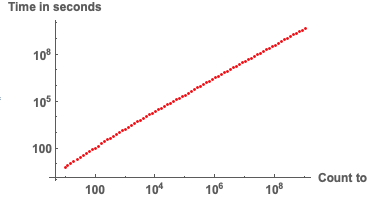
We can also calculate the average time per number if we count up:
averagetime={#[[1]], QuantityMagnitude[UnitConvert[#[[2]], "Seconds"]]/#[[
1]]} & /@ resultsEnglishHighRes;
ListLogLogPlot[averagetime, LabelStyle -> Directive[Bold, Medium],
AxesLabel -> {"Count up to", "<time> per number in secs"}]
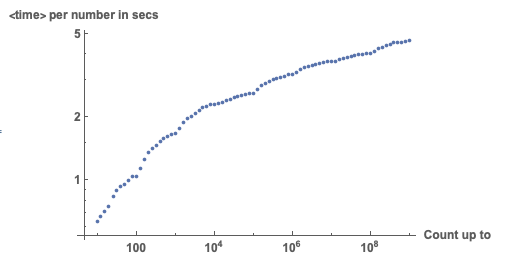
Making this into parenting approved functions
Of course, these graphs tell me how long it takes to count up to a certain number, but they do not allow me to answer my daughter's questions.... So I need to build something to make predictions about how far she has to count until we arrive. We could do some simple curve fitting, but if we are too lazy (and I sure am), we can use Mathematica's more advanced features to get this done - quick and dirty.
Let's try two things:
(i) Let's predict how long we need to count to a certain number. (ii) Predict the number we have to count to if we need to count for a given time.
Let's predict how long we need to count to a certain number
Easy peasy. Here's a predictor
ptime = Predict[
Rule @@@ ({#[[1]], UnitConvert[#[[2]], "Seconds"]} & /@
resultsEnglishHighRes), PerformanceGoal -> "Quality"]
It's ok, but it doesn't give us units so let's do this:
UnitConvert[ptime[1000000],
MixedUnit[{"Years", "Months", "Days", "Hours", "Minutes",
"Seconds"}]]
So this predicts how long I have to count up to a million. I get:
1 mo 11 days 18h 21 min 26.8809s
As before, this won't be as precise as it pretends to be (!) and also is a wee bit different from my direct (but sampled) counting approach, which gave me:
1 mo 6 days 15h 32 min 21.4512 s
But then it is hopefully going to be more precise than the "one-number-per-second" assumption.
Predict the number we have to count to if we need to count for a given time
Luckily there is not much brain-CPU-time required for this either.
preversetime = Predict[Rule @@@ ({QuantityMagnitude[UnitConvert[#[[2]], "Seconds"]], #[[1]]} & /@
resultsEnglishHighRes), PerformanceGoal -> "Quality"]
We can then add units and use units etc as above.
Application
Ok, now here's an hypothetical application - or an experiment which is of course not currently possible due to COVID restrictions.
[planning to drive from Aberdeen to Edinburgh in Scotland]
Clara: "Are we nearly there yet?" Me: "No, we are still in front of our house." Clara: "What do I have to count to?" Me: [takes out phone, opens Wolfram Cloud website (see below)] : "Count to 3573."
Crisis averted. Happy child, happy parent.
Here's how it works:
Ceiling[preversetime[UnitConvert[TravelTime[Entity["City", {"Aberdeen", "AberdeenCity", "UnitedKingdom"}], Entity["City", {"Edinburgh", "Edinburgh", "UnitedKingdom"}]], "Seconds"]]]
Then you deploy that to the Cloud:
CloudDeploy[FormFunction[{"from" -> "Location", "to" -> "Location"},
Ceiling[preversetime[UnitConvert[TravelTime[#from, #to], "Seconds"]]] &], Permissions -> "Public"]
and get a link to a website. Good times!
Conclusion
There are lots of things that can be improved and should be checked. All numbers were computed using a random subsample approach. So we would need to know error bars etc. That can be done, but is out of the scope of this post. We can run some easy tests though. For example:
TravelTime[
Entity["City", {"Aberdeen", "AberdeenCity", "UnitedKingdom"}],
Entity["City", {"Edinburgh", "Edinburgh", "UnitedKingdom"}]]
Gives 2 h 11 mins. The predictor suggests that I should count to 3573. Well, let's quickly do that and see how long it takes:
UnitConvert[Duration[SpeechSynthesize[StringRiffle[StringReplace[IntegerName[#], "\[Hyphen]" -> " "] & /@ Range[3573], ", "]]],MixedUnit[{ "Hours", "Minutes", "Seconds"}]]
That gives 2 h 6 mins 24.2026s (with overwhelming precision!). Not too bad. The code has not been properly beta-tested and there might be bugs. I have not tried to count up to 1000000000 or so to check the results; this is basically due to my very limited life span. Also, I did not even try to make the code nice or efficient. It was basically just typing it in and getting it done - so there are lots of improvements to be made there.
Of course, the cloud version can be adjusted to estimate the number to count to for any given period of time so that it becomes more useful for everyday parenting.
All the best from Scotland, Marco