Dear Wolfram Community:
I have been trying without success in the last week to do some tensor operations on arrays (like the array example at the end). The tensor operations tried include dot product and especially inverse/pseudoinverse. The (pseudo)inverses cannot be done just applying the built-in function into the array, as they are designed just for matrices.
At first I was worried that such operations simply are undefined for arrays other than matrices. Then I found some papers suggesting the following procedure:
1) Do something called "unfolding" to turn the IJK tensor into a (m,n) matrix
2) Invert the matrix
3) Do the inverse operation "fold" to obtain the inverted tensor from the inverted matrix
Unfortunately the notation used for the mapping called "fold" and "unfold" is given by the following, cryptic formulas (taken from Kolda(2006)):
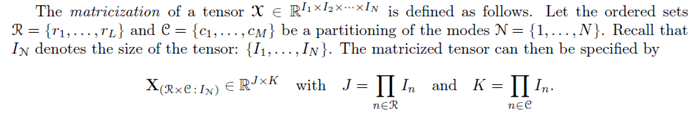
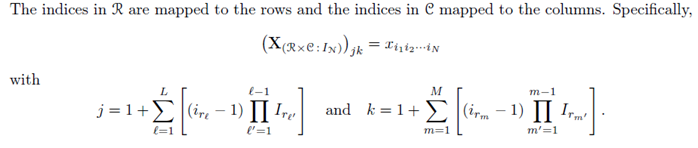
Finally, a code is given, unfortunately in MATLAB and not in Mathematica:

Do someone knows how to "translate" the cryptic formulas of Kolda (2006) or her MATLAB code into a Wolfram Mathematica code?
Thank you in advance.
APPENDIX:
1) References:
*) Tamara G. Kolda (2006); "Multilinear operators for higher-order decompositions "; SANDIA REPORT SAND2006-2081 SANDIA report link
*) Mao-lin Liang, Bing Zheng & Rui-juan Zhao (2018): Tensor inversion and its application to the tensor equations with Einstein product, Linear and Multilinear Algebra
2) Code of the example array I wish to invert:
"1) Example array"
array[T_, m_, v_] := SparseArray[Flatten[{Table[{1 + i, 1, 1} -> T[i, 0, 0], {i, 0, m}], Table[{i + 1, i + 1, 1 + k} -> T[i, i, k], {i, 1, m}, {k, 1, v}]}]]
A4 = array[T, 2, 2];
A4 // MatrixForm