Hi everyone, Since I first read about rulial space and the concept that every possible rule may be applied at the same time, I was dubious about the idea.
You can find these concepts explained in the Project Announcement, or also in Exploring Rulial Space, to get some context.
I had always thought that I had misinterpreted what Wolfram was saying. Maybe he didn't mean that every step, every possible rule is applied. Maybe he just meant that every Turing complete rule is able to emulate the behavior of every other rule, and therefore every rule is equivalent. Then, to us (computationally bounded observers) it is like every rule could be applied every step.
But I recently came across the bulletin Why Does the Universe Exist? where it seems that Wolfram is indeed considering to apply every rule simultaneously.
The reason of my concern about the simultaneous application of all the possible rules is that I feel that this would lead to a trivial universe, that doesn't evolve. Imagine for example to start from the simplest initial condition, an empty hypergraph $\{\}$. You then apply all the possible rules that have $\{\}$ as LHS. For every hypergraph $a$, there will be a rule $\{\} \rightarrow a$, and therefore the second step of the multiway graph will contain every possible hypergraph. For the third step you are now free to apply really every possible rule, since you have every possible LHS available. As a consequence the third step will consist, again, of every possible hypergraph. And each subsequent step will be exactly the same. Hence the system is not evolving anymore. Time is frozen.
This argument may not convince you because treating infinities may be slippery and the state of the a multiway system isn't described just by the collection of states in a particular slice, but also the events that lead there (the causal relations) carry information. I will now address these issues by formalizing the argument.
I will start by defining what I mean by "step" and what I mean when I say that a system is frozen in time, or that it is not evolving anymore.
Definition: multiway step
Given a set of rules $\mathcal{R}$ and a set of spatial hypergraphs $C$, a step is a triplet $(C,E, C')$, where $C'$ is the set of all the spatial hypergraphs that can be obtained by applying a rule $r\in \mathcal{R}$ to an element of $C$, and $E$ is the set of causal events generated by the application of such rules.
In other words, to complete a step you have to apply the rules everywhere they are applicable. This definition of step induces a natural way to foliate a multiway graph, and defines a global time coordinate.
Definition: causally inverted event
Given a rule $r$, one can define the inverted rule $\bar{r}$ that is obtained from $r$ by swapping left hand side and right and side. A similar operation can be done to events. Given two hypergraphs $a$ and $b$, and an event $e: a \rightarrow^r b$, the causally inverted event $\bar{e}$ will be $\bar{e}: b \rightarrow^\bar{r} a$
Definition: frozen system
Consider a multiway system that has evolved for n steps $(C_i,E_i, C_{i+1})$ for $i=1,...,n$. The system at the step n is considered frozen if:
- $C_{n-1} = C_n = C_{n+1}$
- $E_{n}$ can be obtained by $E_{n-1}$ by causally inverting every event of $E_n$.
In a certain sense this definition says that if you invert the direction of time (go from n to n-1 instead that to n+1) and don't notice any difference, then it means that time has stopped, because you cannot distinguish the future from the past.
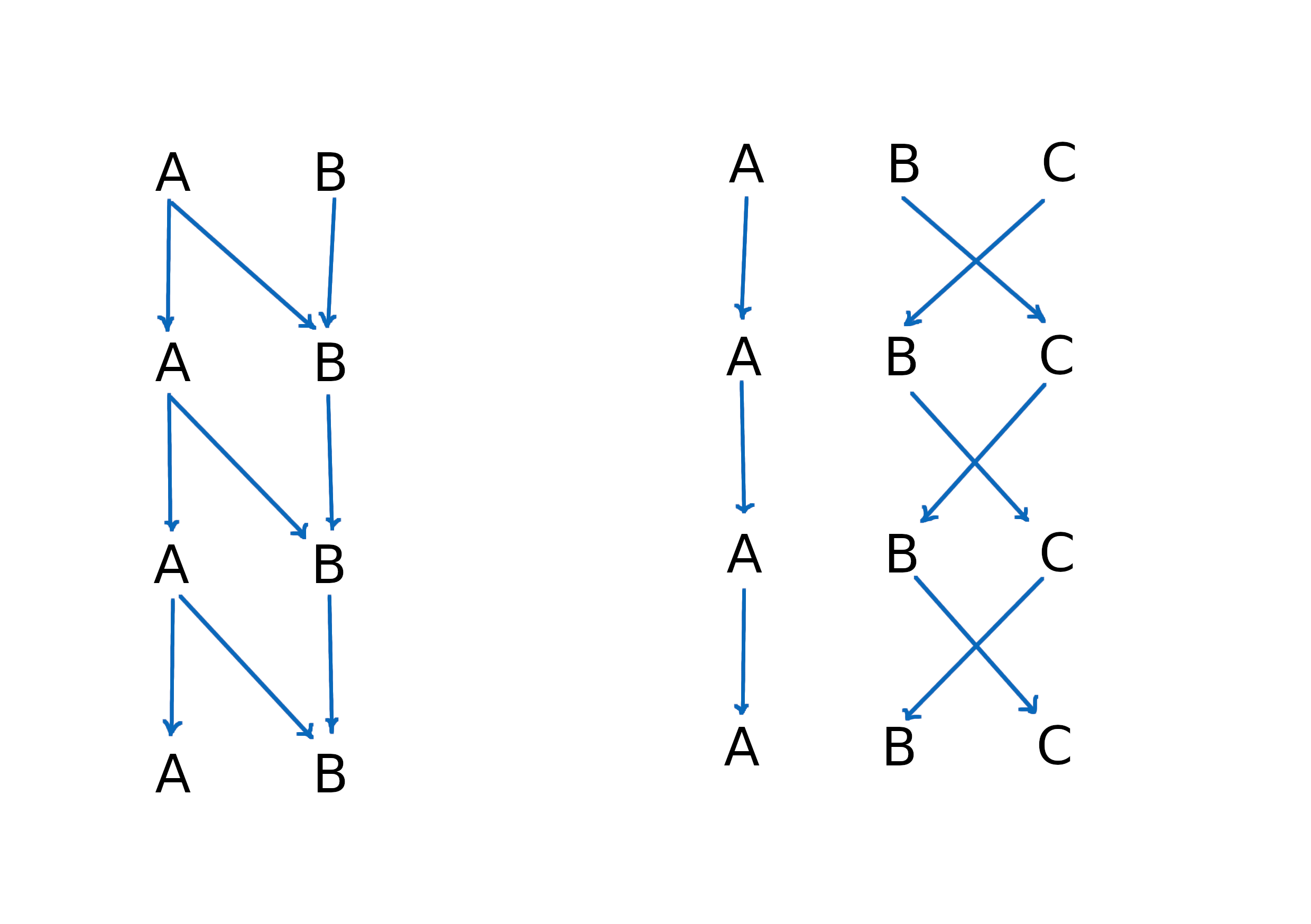 By this definition, the system on the left is not frozen, because it is asymmetric under temporal inversion. The system on the right is instead frozen.
By this definition, the system on the left is not frozen, because it is asymmetric under temporal inversion. The system on the right is instead frozen.
Definition: complete set of rules
Given a set of hypergraphs $C$, the complete set of rules associated with $C$ is the set $\mathcal{R}_C$ defined such that for every couple of hypergraphs $a,b \in C$ there exist a rule $r \in \mathcal{R}_C$, that brings the state $a$ to the state $b$ (in symbols $a\rightarrow^r b$).
It is obvious that if $r \in \mathcal{R}_C$, then also $\bar{r} \in \mathcal{R}_C$.
Theorem: A multiway system with a complete set of rules freezes after the second step
Consider a set of hypergraphs $C$ and its complete set of rules $\mathcal{R}_C$. Choose an hypergraph $c \in C$ as initial condition and evolve the multiway system. Since $\mathcal{R}_C$ is complete, $c$ can be linked to any other hypergraph in $C$, and the first step will then be $( \{ c \} , E_1, C)$, where $E_1$ is the set of events that link $c$ to any hypergraph in $C$.
The second step will be $(C , E_2, C)$ and the third will be $(C , E_3, C)$.
For every $a,b \in C$ there exist a rule $r \in \mathcal{R}_C$ such that the event $e: a \rightarrow^r b$ belongs to $E_2$ and to $E_3$. This means that $E_2=E_3$. Moreover, for every event $e: a \rightarrow^r b$ that belongs to $E_2$, there will also be in $E_3$ the inverted event $\bar{e}: b \rightarrow^\bar{r} a$. In other words, $E_2=E_3$ and they coincide with the set of their inverted events. As a consequence, by the third step the system has frozen.
It is important to notice that I have nowhere assumed that the set of hypergraph or the set of rules must be finite. The whole argument fully applies to infinite set, and in particular it applies to the set of all possible hypergraphs, completed by the set of all possible rules.
Therefore, if we model a universe where, every step, every possible rule is applied, then we can only obtain a trivial, non evolving universe, deprived of any of the complex structures that we observe today in our universe.
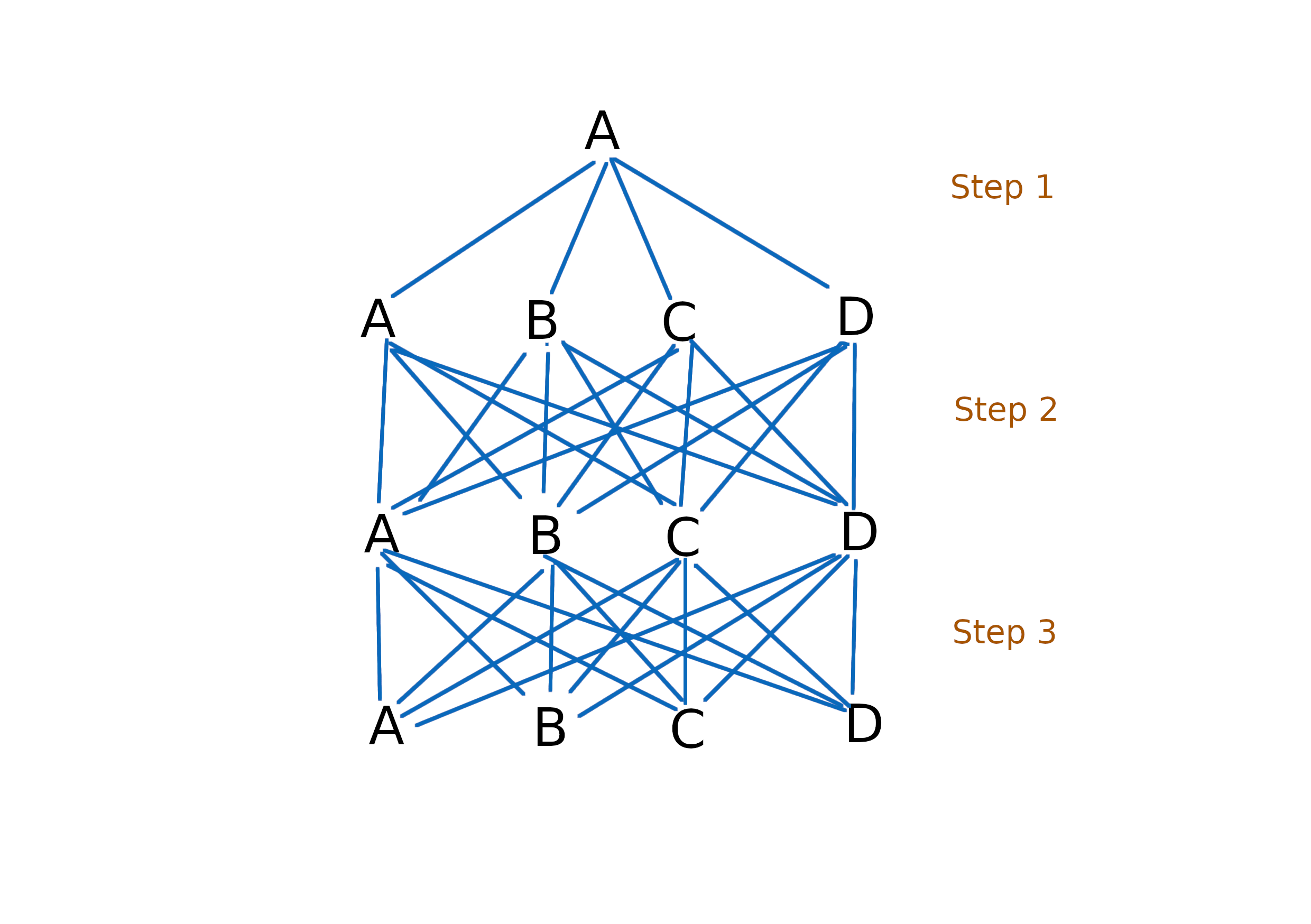 In the figure it is shown an example of complete set of rules, which are: $A \rightarrow A$, $A \rightarrow B$, $A \rightarrow C$, $A \rightarrow D$, $B \rightarrow B$, $B \rightarrow C$, $B \rightarrow D$, $C \rightarrow C$, $C \rightarrow D$, $D \rightarrow D$, plus their inverse. As you can see, by the second step the system started repeating itself, and every step is the same.
In the figure it is shown an example of complete set of rules, which are: $A \rightarrow A$, $A \rightarrow B$, $A \rightarrow C$, $A \rightarrow D$, $B \rightarrow B$, $B \rightarrow C$, $B \rightarrow D$, $C \rightarrow C$, $C \rightarrow D$, $D \rightarrow D$, plus their inverse. As you can see, by the second step the system started repeating itself, and every step is the same.
In Why Does the Universe Exist?, Wolfram wants to address this particular critic that someone may have raised:
What if each piece of our hypergraph is updated according to all possible rules—generating many different possible histories? Or, in other words, what if the universe in some sense “simultaneously runs” all possible rules—generating all possible resulting histories?
Our first instinct might be that if all these possibilities are allowed then there could never be anything definite said about what would happen in the universe. But it turns out that this is far from correct. And it all has to do with the entangling of different possibilities associated with the repeated application of rules.
Given a particular state of the universe, applying different rules can lead to different states. But applying rules to different states can also potentially lead to the same state. Or, in other words, the “rulial multiway graph” that represents how one state leads to another can exhibit both branching and merging.
I am not able to see how the merging of the multiway branches could provide structure to a multiway system with a complete set of rules, which, by the theorem just proven, is required to freeze by the third step. Additionally, Wolfram makes two examples, but the first does not have a complete set of rules, so I don't think it is suited to prove that complete sets of rules can generate nontrivial structure. The second example is instead complete, and therefore freezes after the second step. What Wolfram refers to as a "more symmetrical structure", is just a complete graph, the signature that the system is not evolving anymore.
Any thoughts on that? Have I misinterpreted Wolfram? Does the concept of simultaneous application of every possible rule need to be abandoned?