Problem#2.
2nd problem in this collective thread, see the "What would make this equation true??"-video:
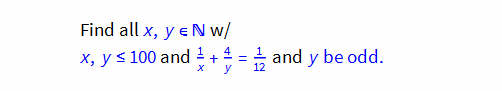
Commenting the OddQ[] part outputs all solutions, from which one could pick the odd y solution, namely y=57:
In[1]:= FindInstance[{(*OddQ[y] == True,*) 0 <= x <= 100, 0 <= y <= 100, 1/x + 4/y == 1/12}, {x, y}, Integers, 100]
Out[1]= {{x -> 24, y -> 96}, {x -> 28, y -> 84}, {x -> 30, y -> 80}, {x -> 36, y -> 72}, {x -> 44, y -> 66}, {x -> 48, y -> 64}, {x -> 60, y -> 60}, {x -> 76, y -> 57}, {x -> 84, y -> 56}}
But when I uncomment in the above code, there is no result. Basically I am asking: How do we define in set of equations a variable to assume odd integer values only, for use in mathematical expressions or equations within Solve[], Reduce[], Simplify[], FindInstance[]etc.?