Currently I have several numerical engines my mac, including Mathematica itself
(use some MKL kernel), customized LAPACK library in System Modeler and the OSX's native Accelerator framework.
I wrote several programs here to compare decomposed results in different forms. No intend to find performance. Should this article be helpful for those want to transfer results among these computing platforms. QR decomposition is chosen here because this matrix transformation does not gurantee a unique output for a given input. This discussion is also inspired by
this thread. Wolfram LanguageMy test data is a 5-by-5 matrix generated by

Just use the build-in function to find the orthognal matrix Q and the right upper triangle:

For matrices on Real domain, we can simply verify with the following:

Note that Mathematica uses row-based arrangement, which perfectly follows C/C++ standard and other common notation.
Wolfram System Modeler
We can also decompose the matrix by using the LAPACK library bundled with System Modeler. Once you have the System modeler open and drag model and function into the User Class section, you can quickly call them via Mathematica's WSMLink seamlessly by the name of the classes/model. Here the QRDModel calls the myQRD function, you just need to load the name of the model only.
<< WSMLink`
mmodel = "myLapackQRDModel";
sim = WSMSimulate[mmodel, {0, 1}] // Quiet;
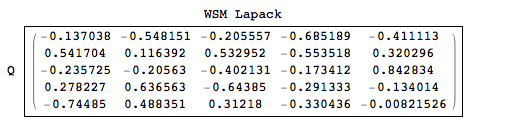
I have the following outputs, each one is an entry to the output matrix.
sim["VariableNames"][[1;;25]]
{b[1,1],b[1,2],b[1,3],b[1,4],... b[5,5]}
Define an auxillary function below to extract the variable trajectory. Each variable is a function of time but with constant value, so you set an arbitary time point, you can check out the value of the entry.
f[i_,j_]:=(sim[{"b["<>ToString[i]<>","<>ToString[j]<>"]"}])[[1]]
You can see that the Q here is slightly different from what we had from Mathematica. This means the Lapack method chooses a different pivoting scheme and assembled the Q with somewhat different Household elements
Q2 = Table[f[i, j][0.5], {i, 1, 5}, {j, 1, 5}];
Labeled[Framed[Chop[Q2] // MatrixForm], {"WSM Lapack", "Q"}, {Top,
Left}]
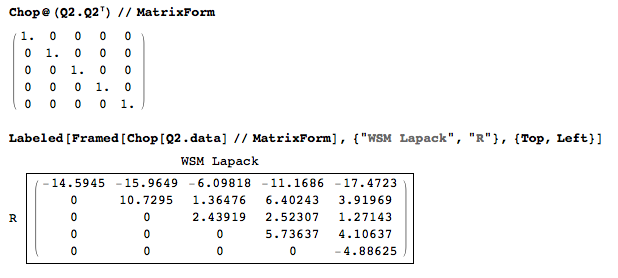
Verify if the new Q is unitarian and orthonormal:
In the WSM example, I actually call an external cpp file. A C/C++ interface is very useful and add flexibility for more control for experience C users.
Accelerate Framework: <Accelerate/Accelerate.h>Last part is about the build-in free LAPACK on OSX 10.6+ . You can run the QRDecomp.cpp and the print out result into this notebook on mac. If you are on Linux or Win then you can use "-L/lapack/dir -lLAPACK" flag if you know where a libLapack.a file is installed. Otherwise "-framwork Accelerate" is all you need to complile the cpp file.

Verify the Unitarian property:

The default R matrix is not strictly an right - upper triangle but requires permutation matrix P:
A*P = Q*R
This piece of information about P is usually found in the updated value of the "jpvt" argument in "dgeqpf_".
dgeqpf_(&nRow, &nCol, output_Matrix, &nRow, jpvt, tau, work, &info); // C code
 Very Important : Array arrangement
Very Important : Array arrangementIf you find a
documentation about calling fortran LAPACK function, you have to be very careful about handling array arrangement. You usually have to transpose the matrix you see in Mathematica and C as input for the LAPACK/BLAS and their C version. You do not need to transpose the intermediate result. Also in this note book, I do not transpose the output matrix because I want to have (A = Q\*R ) or (Q*A = R ) so that the latter two results can be used as the native output by Mathematica. Just be aware that the array arrangement are different and sometimes you need to test little bit to find what you have matches your convention.
Code snippets: myLapackQRDModel.mo
model myLapackQRDModel
Real y[5,5]=__test_data__;
Real b[5,5];
algorithm
b:=myQRD(transpose(y));
end myLapackQRDModel;
myQRD.mo
function myQRD
input Real a[:,:];
output Real b[size(a, 1),size(a, 2)];
external "C" myQRD(size(a, 1),size(a, 2),a,b) annotation(Include="#include \"myQRD.cpp\"", Library="LAPACK");
end myQRD;
myQRD.cpp #include <stdlib.h>
#define MIN(a,b) ((a) < (b) ? (a) : (b))
extern "C" {
// for QR decomposition
int dgeqpf_(int *m, int *n, double *a, int *lda, int *jpvt, double *tau, double *work, int *info);
int dorgqr_(int *m, int *n, int *k, double *a, int *lda, double *tau, double *work, int *lwork,
int *info);
}
void myQRD(int m,int n, double *matrix, double* b) {
int error=1;
int *jpvt = new int[n]; //pivot matrix
double *tau = new double[MIN(n,m)];
double *work = new double[3*n]; //working array
int info=1; // find which col has illegal value
int i;
for (i=0;i<m*n;i++) b[i] = matrix[i];
/* dgeqpf */
int nRow = m;
int nCol = n;
error = dgeqpf_(&nRow, &nCol, b, &nRow, jpvt, tau, work, &info);
delete[] work;
/* dorgqr */
int k = MIN(n,m);
int lwork= MIN(10, nCol)*nCol;
double *work2 = new double[lwork];
dorgqr_(&nRow, &nCol, &k, b ,&nRow, tau, work2, &lwork,&info);
delete[] work2;
}
C++ test for Mac user This is a standalone test code. To compile, you need the following command:
g++ -o QRDExample QRDecomp.cpp -framework Accelerate
QRDecomp.cpp // QRDecomp.cpp
#include <iostream>
#include <Accelerate/Accelerate.h>
#define MIN(a,b) ((a) < (b) ? (a) : (b))
void myQRD(int m,int n, double *matrix, double* b);
int main(int argc, const char * argv[])
{
double data[5][5] = < copy the __test_data__ and paste here >
int m = 5;
int n = 5;
// flatten the data array
double* input = new double[m*n];
// store the result
double* Res = new double[m*n];
//transpose the data array as an input to the myQRD function
int i, j;
for(i=0;i<m;i++ ){
for(j=0; j< n; j++){
input[ i * m + j ] = data[j][i];
}
}
// find QR decomp
myQRD(m,n,input, Res);
//print out result, can be pasted into Mathematica
std::cout<<"{";
for(i=0;i<m;i++ ){
std::cout<<"{";
for(j=0; j<n; j++){
((j == n-1) ? std::cout<< Res[m*i+j]:std::cout<< Res[i*m+j]<<"," );
}
std::cout<<"},\n";
}
std::cout<<"}";
return 0;
}
void myQRD(int m,int n, double *matrix, double* b) {
/**** Same as the myQRD() in myQRD.cpp ****/
}
Code can be downloaded from the attachment link.
 Attachments:
Attachments: