One online community in China posted the following problem:
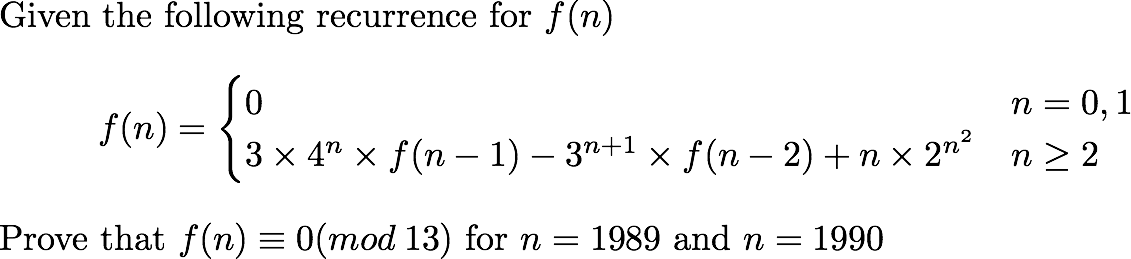
Apparently the problem cannot be solved using brutal force because the coefficients grows drastically, typically the last term grows even faster than the regular exponential. Because the problem is asking about the module of f(n), I guess it would be easy to handle the f(n) mod 13 than f(n) in this case.
Use the following homomorphism of the module function:
Mod[a * b, 13] === Mod[a,13] * Mod[b,13]
Mod[a + b, 13] === Mod[a,13] + Mod[b,13]
I can define the f(n) as following with caching:
Clear[f]
f[0] = f[1] = 0;
f[v_] := f[v] =
3*Mod[4^v, 13]*Mod[f[v - 1], 13] - Mod[3^(v + 1), 13]*Mod[f[v - 2], 13] + Mod[v, 13]*Mod[2^(v^2), 13]
The default recurrence limit is 1024, therefore, I need to set the recursion limit to a higher number or infinity.
In[1]:= Block[{$RecursionLimit=Infinity},{Mod[f[1989],13],Mod[f[1990],13]}]
Out[1]= {0,0}
Wolfram language ususally solve this type of problem in a fraction of second. But if the problem is asking a larger number, caching may cause large memory consumption. To prevent overflow, I can adopt a concise and elegant way of doing this in "pure functional style".
Recall Fibonacci sequence
Fib[n] = Fib[n-1] + Fib [n-2] with F[1] = F[2] = 1
Instead of using function definition with the recurrence, we can use the Rule + Anonymous function.
{1,1,3}//.{a_,b_,n_}:> If[n<10,{b, a+b, n+1},Print[{n-1, b}]]
{9,34}
( Fibonacci[9] = 34 )
Here the ReplaceRepeated (//.) constantly update the {a,b,n} list until n is larger than 10. Because the If function returns exactly the same form of {a,b,n} every time, the update would not stop. Once n hits 10, the Print functions is called and returns a NULL, which is not the form of {a,b,n}. Hence, the iteration halts.
Similarly, I can use the same thing for this problem
{0,0,2}//.{a_,b_,n_}:>
If[n<1990,
{b,3*Mod[4^n,13]*Mod[b,13]-Mod[3^(n+1),13]*Mod[a,13]+Mod[n,13]*Mod[2^Mod[n,12]^2,13],n+1},
Row[{"f[",n-1,"] mod 13 = ",Mod[ b,13]}]
]
--> f[1989] mod 13 = 0
Add a MaxIterations option to remove the cap of iteration count:
ReplaceRepeated[
{0,0,2},
{a_,b_,n_}:>If[n<70000,
{b,3*Mod[4^n,13]*Mod[b,13]-Mod[3^(n+1),13]*Mod[a,13]+Mod[n,13]*Mod[2^Mod[n,12]^2,13],n+1},
Row[{"f[",n-1,"] mod 13 = ",Mod[ b,13]}]
],MaxIterations->Infinity
]
--> f[69999] mod 13 = 6
To make the computation even faster, I shall use the lightweighted coefficients. Under modular transformation, the simple power term can be found with cyclic residues easily:

The power function thus reduces to
{List of Number}[[ Mod[v, Period, 1 ] ]]
The last term in recurrence is tricky. We can first visualize its cyclic property. The framed part reveals the repeated pattern.
DiscretePlot[Mod[v*2^(v^2), 13], {v, 1, 120}]
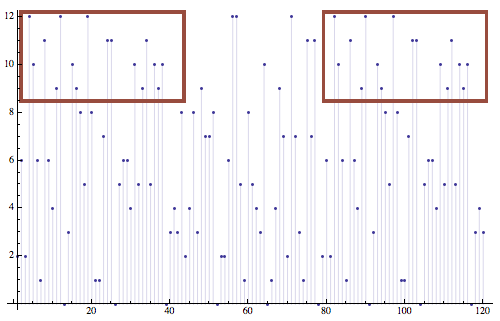
On the other hand, one can prove this pattern does exist: the complete congruence family of 2^p with module 13 is the following, which has a period 12:

Therefore we just to check the family of residues of v^2 about 12:

The result means that only the first, fourth, nineth and the last item in list A (red numbers) are possible values and the period is 6, which denoted by the red numbers in list B. The only possible residue of 2^(v^2) are
{2,4,8,3,6,12,11,9,5,10,7,1}[[#]]&/@({1,4,9,4,1,0}/.{0-> 12})
--> {2,3,5,3,2,1}
The peoriod of the compound expression thus can be no longer than 6 * 13 = 78. In this case the peorid is 78 (length of the red italic numbers):
 The complete code set can be found in the attachment link below.
The complete code set can be found in the attachment link below.
 Attachments:
Attachments: