
The above photo of an arrangement on my desk looks inspired by René Magritte's surrealistic painting "Ceci n'est pas une pipe": none of the 4 images are a real "Utah Teapot". Two of them are anamorphic figures and the other two are their reflections in a cylindrical mirror. In what follows I will explain how this "treacherous image" was made using Mathematica.
The 4 images are originating from the teapot code below (a set of 432 polygons):
teapot = ExampleData[{"Geometry3D", "UtahTeapot"}, "PolygonObjects"];
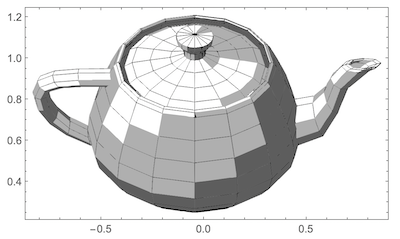
teapot3D = Graphics3D[teapot, Boxed -> False, ViewPoint -> {0, 10, 8}]

The 3D image is converted into a 2D Graphics object using ImageGraphics:
im = ImageReflect[ColorConvert[Image[teapot3D], "Grayscale"], Left];
ig = Rest[
Normal@
First[ImageGraphics[ImageCrop@im, Method -> "LinearSeparable"]]];
scaledIg2D = ig /. {x_?NumericQ, y_} :> {x - 500, y + 150}/650;
Graphics[scaledIg2D, Frame -> True]
The following function cylinderAnamorphPoint2D computes the anamorphic point A in the x-y plane from its reflection R in an upright cylindrical mirror of radius 1. The observer's eye at viewpoint V will see A reflected as R in the cylindrical mirror. Q is the intersection point of the incident ray VR with the cylinder. The law of reflection requires equal angles between VR and and the reflected ray QA with the normal n at Q. All points on the reflected half-line QA are in fact anamorphic points of R and will be observed as R if seen from V.
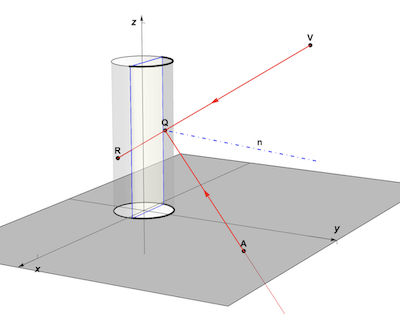
cylinderAnamorphPoint2D[ptR : {xi_, yi_, zi_}, ptV : {0, yv_, zv_}] :=
Module[{ptQ, ptVr},
(*intersection cyl-viewline*)
ptQ = Nearest[
NSolveValues[{Element[{x, y, z}, HalfLine[{ptR, ptV}]] &&
x^2 + y^2 == 1.}, {x, y, z}], ptV][[1]];(*reflection of V-
Q in normal n at Q*)
ptVr = ReflectionTransform[ReplacePart[ptQ, 3 -> 0], ptQ][ptV];
(*intersection reflection line with x-y plane*)
First[NSolveValues[{Element[{x, y, z}, HalfLine[ptQ, ptQ - ptVr]] &&
z == 0}, {x, y, z}]]]
The 2D anamorphic image of the teapot is obtained by mapping the function cylinderAnamorphPoint2D to the point coordinates of the scaled Graphics object scaledIg2D:
igAnam2D =
DeleteCases[scaledIg2D,
Line[{{_?NumericQ, y_}}], \[Infinity]] /. {x_?NumericQ,
y_?NumericQ} :>
cylinderAnamorphPoint2D[{x, .125, y}, {0, 10, 8.}];
Graphics[{Circle[],
igAnam2D /. {x_?NumericQ, y_?NumericQ, 0.} :> {x, y}}]
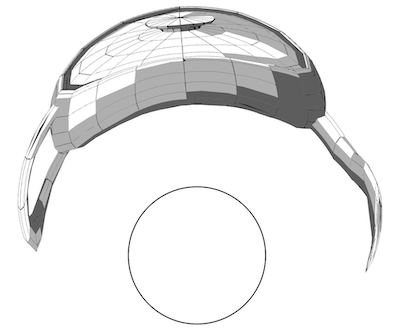
With the eye at the right viewpoint, the above 2D image reflects as a 3D image of the teapot. Here is how it looks like:

An infinite amount of images or objects can reflect in a cylinder as the original teapot. This is the result of the geometry explained above and its conclusion: "All points on the reflected half-line QA are in fact anamorphic points of R and will be observed as R if seen from V". In a previous Community Contribution: "Anamorphosis of 3D-Objects & 3D Printing", I demonstrated how a deformed 3D printed object will also reflect as the original teapot.

To obtain a 3D anamorphic object, we make a new function cylinderAnamorphPoint3D, a slight adaptation of the function cylinderAnamorphPoint2D: find a point on the reflection line with its original z-coordinate i.o. one in the x-y plane (with z=0):
cylinderAnamorphPoint3D[ptR : {xi_, yi_, zi_}, ptV : {0, yv_, zv_}] :=
Module[{ptQ, ptVr},
(*intersection cyl-viewline*)
ptQ = Nearest[
NSolveValues[{Element[{x, y, z}, HalfLine[{ptR, ptV}]] &&
x^2 + y^2 == 1.}, {x, y, z}], ptV][[1]];(*reflection of V-
Q in normal n at Q*)
ptVr = ReflectionTransform[ReplacePart[ptQ, 3 -> 0], ptQ][ptV];
(*intersection reflection line with x-y plane*)
First[NSolveValues[{Element[{x, y, z}, HalfLine[ptQ, ptQ - ptVr]] &&
z == zi}, {x, y, z}]]]
After mapping both functions to the polygon vertices of the teapot, we get both the 2D anamorphic print in the x-y plane and the 3D anamorphic object. Both will reflect in the cylindrical mirror as the original teapot.
igAnam2D3D =
teapot /. {x_?NumericQ, y_, z_} -> {x - .5, y, z} /. {x_?NumericQ,
y_?NumericQ, z_} :>
cylinderAnamorphPoint2D[{x, y, z}, {0, 10, 8.}];
igAnam3D =
teapot /. {x_?NumericQ, y_, z_} -> {x - .5, y, z} /. {x_?NumericQ,
y_?NumericQ, z_} :>
cylinderAnamorphPoint3D[{x, y, z}, {0, 10, 8.}];
Graphics3D[{(*floor plane *){Opacity[0.25], Gray,
InfinitePlane[{0, 0, 0}, {{1, 0, 0}, {0, 1, 0}}]},
(*cylinder*){Opacity[0.15], Cylinder[{{0, 0, 0}, {0, 0, 2}}, 1]},
(*cylinder base*){Opacity[.15],
Scale[{EdgeForm[AbsoluteThickness[.5]],
Cylinder[{{0, 0, 0}, {0., 0., 0}}, 1]}, {1, 1, 1}, {0, 0,
0}]}, {EdgeForm[Black], FaceForm[MaterialShading["Clay"]],
teapot, igAnam2D3D, igAnam3D}}, Boxed -> False,
Lighting -> "Neutral", ViewPoint -> {0, 2, .75},
ViewVertical -> {0, 0, 1}]
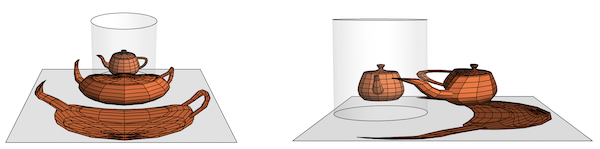
The following photos show that both the B&W 2D print and the blue 3D anamorphic printout reflect as the original teapot. Both reflections coincide If observed from the right viewpoint (upper left photo). The 3 pictures at the bottom show the separation of the reflections as the viewpoint moves up from the ideal. The upper right picture is a side-view of the arrangement.

Just to show : "nothing is as it appears". Or as Magritte demonstrated : a painting of a pipe is not a pipe!