Message Boards Message Boards

Almost indisputable proof of the half-hex cellular automaton

Brad Klee, Wolfram Research
Posted 2 years ago
POSTED BY: Brad Klee
3 Replies
Sort By:

enter image description here -- you have earned Featured Contributor Badge enter image description here Your exceptional post has been selected for our editorial column Staff Picks http://wolfr.am/StaffPicks and Your Profile is now distinguished by a Featured Contributor Badge and is displayed on the Featured Contributor Board. Thank you!
POSTED BY: Moderation Team

Here are a few more static plane filling C.A.'s, for the chair tiling (or if you prefer, for the trilobite and crab tiling):

tilted1

The above uses Von-Neumann neighborhood. It can be transformed into the following:

Chair dual

With black for crabs without orientation and colors for trilobites with orientations. When orientations of trilobites are known, orientation of crabs can be obtained by propagating termination signals through channels of the tiling. Another way to evolve the same pattern is as follows:

enter image description here

However notice there is a slight time delay on propagation of colors. This is not really a problem, so perhaps the last solution is the best.

POSTED BY: Brad Klee

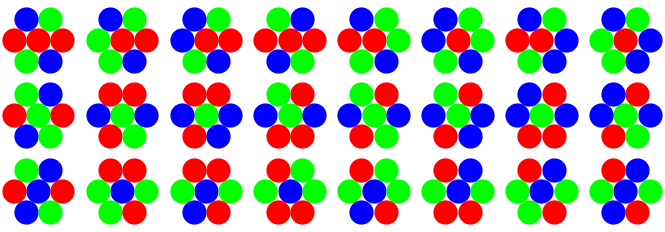
half hex atlas

Half Hex Atlas

The following code is a slightly less-involved derivation of apparently the same rules seen above. (Equivalence of rule sets can be verified in practice by comparing counting functions for sufficiently long time intervals). See also: Whole Hex Rule Derivation.

star = ReIm[Exp[I 2 Pi #/3]] & /@ Range[0, 2];

ToCanonical[vec_] := Subtract[vec, Floor[Divide[vec.{1, 1, 1}, 3] ]]

NeighborLocs[or_, 1] := Map[ToCanonical[or + #] &,
  Riffle[IdentityMatrix[3], RotateRight[-IdentityMatrix[3]]]]

NeighborLocs[or_, n_] := Join[NeighborLocs[or, n - 1],
  Flatten[Partition[NeighborLocs[or, 1], 3, 1, 1]
    /. {x_List, y_List, z_List} :> Map[
      ToCanonical[or + n x + # z] &, Range[0, n - 1]], 1]]

InfM = RotateRight[{2, 0, 0}, #] & /@ Range[0, 2];

InflateRep = {T[x_, v_] :> Prepend[Join[
      T[ToCanonical[InfM.x] + IdentityMatrix[3][[#]], #] & /@ Range[3],
      T[ToCanonical[InfM.x] - IdentityMatrix[3][[#]], #] & /@ 
       Range[3]],
     T[ToCanonical[InfM.x], v]]};

Depict[v_, c_] := {c /. {1 -> Red, 2 -> Green, 3 -> Blue, 0 -> White},
    Disk[v.star, 1/2]};

tilingData = NestList[Union[Flatten[# /. InflateRep]] &,
   T[{0, 0, 0}, 1] /. InflateRep, 4];

NeighborVals[data_, or_] := With[{locs = NeighborLocs[or, 1]},
  ReplaceAll[Cases[data, T[#, dir_] :> dir], {} -> {0}][[1]] & /@ locs]

GetTemplates[data_] := Union[Select[
   NeighborVals[data, #[[1]] ] -> #[[2]] & /@ data,
   ! MemberQ[#[[1]], 0] &]]

AbsoluteTiming[
 templates = GetTemplates /@ tilingData[[1 ;; 4]];
 Length /@ templates;]

DepictTemplate[rule_] := Graphics[{
   Depict[{0, 0, 0}, rule[[2]]],
   MapThread[Depict, {NeighborLocs[{0, 0, 0}, 1], rule[[1]]}]
   }, ImageSize -> 75]

SortedInds = 
  Cases[Position[templates[[-1]], #], {x_, 2} :> x] & /@ Range[1, 3];

GraphicsGrid[
  Partition[DepictTemplate /@ templates[[-1, Flatten[SortedInds]]], 
   8]];

partials[temp_] := 
 ReplacePart[temp, Alternatives @@ # -> _] & /@ Subsets[Range[6]] 

AllPartials = 
  Union[Flatten[partials /@ templates[[3, SortedInds[[#]], 1]], 
      1]] & /@ Range[3];

FilteredPartials = Complement[AllPartials[[#]],
     Flatten[AllPartials[[Complement[Range[3], {#}]]] , 1] ] & /@ 
   Range[3];

Subsets[Range[3], {2}] /. {{x_, y_} :> 
    Intersection[FilteredPartials[[x]], FilteredPartials[[y]]]};

DefiniteRules = {Alternatives @@ FilteredPartials[[1]] -> 1,
   Alternatives @@ FilteredPartials[[2]] -> 2,
   Alternatives @@ FilteredPartials[[3]] -> 3};

OnRules = Flatten[
   Outer[RotateRight[{#2, 0, 0, 0, 0, 0}, #1] -> 
      RotateLeft[Range[3], #1][[1]] &, Range[0, 5], Range[3]]];

ExtRules = Join[Map[
    RotateLeft[{RotateRight[Range[3], #][[1]], 
        RotateRight[Range[3], #][[2]], 0, 0, 0, 0}, #] -> 
      RotateRight[Range[3], #][[3]] &, Range[0, 5]], Map[
    RotateLeft[{RotateRight[Range[3], #][[2]], 
        RotateRight[Range[3], #][[1]], 0, 0, 0, 0}, #] -> 
      RotateRight[Range[3], #][[3]] &, Range[0, 5]]];

CollideRules = Map[
   RotateLeft[{RotateRight[Range[3], #][[1]], 0, 0, 
       RotateRight[Range[3], #][[1]], 0, 0}, #] -> 
     RotateRight[Range[3], #][[1]] &, Range[0, 2]];

AllRules = Join[DefiniteRules,
   OnRules /. {2 -> 3, 3 -> 2},
   ExtRules /. {2 -> 3, 3 -> 2},
   CollideRules /. {2 -> 3, 3 -> 2}];

State0 = {{T[{0, 0, 0}, 1]}, {}};

Iterate[state_] := With[{newVerts = Complement[
     Flatten[NeighborLocs[#, 1] & /@ state[[1, All, 1]], 1],
     Flatten[state[[All, All, 1]], 1]]},
  Flatten /@ {MapThread[
     If[IntegerQ[#2], T[#1, #2], {}] &, {newVerts, 
      ReplaceAll[NeighborVals[Flatten[state], #],
         AllRules] & /@ newVerts}], state}]

Graphics[Flatten[Nest[Iterate, State0, 4 #]] /. T -> Depict] & /@ 
  Range[5];

GrowthData65 = NestList[Iterate, State0, 65];

Complement[Flatten[GrowthData65[[-1]]], 
 Nest[Flatten[# /. InflateRep] &, T[{0, 0, 0}, 1], 7]] 

Out[]={}

Length[#[[1]] ] & /@ GrowthData65
%[[2 ;; -1]]/6
Flatten[Position[%, 3]]
Differences[%]

Out[]={1, 6, 12, 18, 24, 18, 42, 48, 48, 18, 42, 66, 90, 60, 120, 108, 96,
18, 42, 66, 90, 66, 162, 186, 186, 60, 138, 216, 264, 162, 276, 228, 
192, 18, 42, 66, 90, 66, 162, 186, 186, 66, 162, 258, 354, 234, 474, 
426, 378, 60, 138, 216, 282, 234, 528, 600, 552, 162, 366, 570, 630, 
366, 588, 468, 384, 18}

Out[]={1, 2, 3, 4, 3, 7, 8, 8, 3, 7, 11, 15, 10, 20, 18, 16, 3, 7, 11, 15, 
11, 27, 31, 31, 10, 23, 36, 44, 27, 46, 38, 32, 3, 7, 11, 15, 11, 27, 
31, 31, 11, 27, 43, 59, 39, 79, 71, 63, 10, 23, 36, 47, 39, 88, 100, 
92, 27, 61, 95, 105, 61, 98, 78, 64, 3}

Out[]={3, 5, 9, 17, 33, 65}

Out[]={2, 4, 8, 16, 32}

The last output shows log-periodicity with inflation factor $2$, thus the C.A. does have what we called "Ulam Structure" elsewhere. For reference, the $85$ derived rules are:

AllRules2

Out[]={
{0, 0, 0, 0, 0, 1} -> 2
{0, 0, 0, 0, 1, 0} -> 3
{0, 0, 0, 1, 0, 0} -> 1
{0, 0, 1, 0, 0, 0} -> 2
{0, 1, 0, 0, 0, 0} -> 3
{1, 0, 0, 0, 0, 0} -> 1
{0, 0, 0, 0, 0, 2} -> 2
{0, 0, 0, 0, 2, 3} -> 1
{0, 0, 0, 0, 3, 0} -> 3
{0, 0, 0, 3, 1, 0} -> 2
{0, 0, 1, 2, 0, 0} -> 3
{0, 0, 2, 0, 0, 0} -> 2
{0, 2, 3, 0, 0, 0} -> 1
{0, 3, 0, 0, 0, 0} -> 3
{2, 0, 0, 0, 0, 1} -> 3
{3, 1, 0, 0, 0, 0} -> 2
{0, 0, 0, 0, 1, 3} -> 2
{0, 0, 0, 0, 2, 1} -> 3
{0, 0, 0, 2, 1, 0} -> 3
{0, 0, 0, 3, 2, 0} -> 1
{0, 0, 1, 3, 0, 0} -> 2
{0, 0, 3, 2, 0, 0} -> 1
{0, 1, 3, 0, 0, 0} -> 2
{0, 2, 1, 0, 0, 0} -> 3
{2, 0, 0, 0, 0, 3} -> 1
{2, 1, 0, 0, 0, 0} -> 3
{3, 0, 0, 0, 0, 1} -> 2
{3, 2, 0, 0, 0, 0} -> 1
{0, 0, 0, 0, 3, 2} -> 1
{0, 0, 0, 1, 3, 0} -> 2
{0, 0, 2, 1, 0, 0} -> 3
{0, 3, 2, 0, 0, 0} -> 1
{1, 0, 0, 0, 0, 2} -> 3
{1, 3, 0, 0, 0, 0} -> 2
{0, 0, 0, 2, 2, 3} -> 1
{0, 0, 0, 3, 1, 1} -> 2
{0, 0, 1, 2, 2, 0} -> 3
{0, 0, 3, 3, 1, 0} -> 2
{0, 1, 1, 2, 0, 0} -> 3
{0, 2, 3, 3, 0, 0} -> 1
{2, 0, 0, 0, 1, 1} -> 3
{2, 2, 0, 0, 0, 1} -> 3
{2, 2, 3, 0, 0, 0} -> 1
{3, 0, 0, 0, 2, 3} -> 1
{3, 1, 0, 0, 0, 3} -> 2
{3, 1, 1, 0, 0, 0} -> 2
{0, 0, 1, 3, 1, 3} -> 2
{0, 2, 1, 2, 1, 0} -> 3
{2, 0, 0, 3, 2, 3} -> 1
{2, 1, 0, 0, 2, 1} -> 3
{3, 1, 3, 0, 0, 1} -> 2
{3, 2, 3, 2, 0, 0} -> 1
{0, 0, 0, 2, 1, 1} -> 3
{0, 0, 0, 2, 2, 1} -> 3
{0, 0, 3, 2, 2, 0} -> 1
{0, 0, 3, 3, 2, 0} -> 1
{0, 1, 1, 3, 0, 0} -> 2
{0, 1, 3, 3, 0, 0} -> 2
{2, 1, 1, 0, 0, 0} -> 3
{2, 2, 0, 0, 0, 3} -> 1
{2, 2, 1, 0, 0, 0} -> 3
{3, 0, 0, 0, 1, 1} -> 2
{3, 0, 0, 0, 1, 3} -> 2
{3, 2, 0, 0, 0, 3} -> 1
{0, 0, 3, 3, 1, 1} -> 2
{0, 1, 1, 2, 2, 0} -> 3
{2, 2, 0, 0, 1, 1} -> 3
{2, 2, 3, 3, 0, 0} -> 1
{3, 0, 0, 2, 2, 3} -> 1
{3, 1, 1, 0, 0, 3} -> 2
{0, 0, 1, 2, 2, 1} -> 3
{0, 0, 2, 0, 0, 2} -> 2
{0, 0, 3, 2, 2, 3} -> 1
{0, 1, 3, 3, 1, 0} -> 2
{0, 2, 3, 3, 2, 0} -> 1
{0, 3, 0, 0, 3, 0} -> 3
{1, 0, 0, 1, 0, 0} -> 1
{2, 0, 0, 2, 1, 1} -> 3
{2, 1, 1, 2, 0, 0} -> 3
{2, 2, 1, 0, 0, 1} -> 3
{2, 2, 3, 0, 0, 3} -> 1
{3, 0, 0, 3, 1, 1} -> 2
{3, 1, 0, 0, 1, 3} -> 2
{3, 1, 1, 3, 0, 0} -> 2
{3, 2, 0, 0, 2, 3} -> 1
}
POSTED BY: Brad Klee
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract