ClearAll["Global`*"];
\[Epsilon] = 0.5;
\[Beta] = 45;
\[Lambda] = 1;
F = 2000;
Nu = 829440/(
103680 - 8640 \[Epsilon]^2 + 3960 \[Epsilon]^4 + 297 \[Epsilon]^6 +
40 F^2 \[Epsilon]^6 \[Lambda]^2 +
40 F^2 \[Epsilon]^6 \[Lambda]^2 Cos[2 \[Beta]]);
T1 = Nu (1 /4 (1 - r^2) + \[Epsilon] 1 /
8 (r^3 -
r) Sin[\[Zeta]] + \[Epsilon]^2 (1 /
24 Cos[2 \[Zeta]] (r^4 - r^2) + (r^2/16 - r^4/32 - 1/32)));
ContourPlot[T1, {r, -1, 1}, {\[Zeta], 0, 2 Pi}, ContourLabels -> True,
PlotTheme -> "Scientific", PlotPoints -> 10]`.
I want to contour plot T in circle geometry not in Cartesian. For example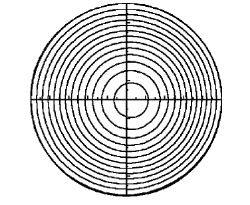 .
.
I am attaching the file too. Please Help!