Hi,
there are issues with convergence with your parameters. I have modified the start conditions to your start time and that seems to work ok.
n = 67000000
cases = {713, 1089, 812, 1182, 1033, 1288, 1160, 853, 1184, 1048,
1522, 1276, 1108, 1715, 1406, 1295, 1508, 1735, 1940, 1813, 2988,
2948, 2460, 2659, 2919, 3539, 3497, 3330, 2621, 3105, 3991, 3395,
4322, 4422, 3899, 4368, 4926, 6178, 6634, 6874, 6042, 5693, 4044,
7143, 7108, 6914, 6968, 12872, 22961, 12594, 14542};
time = {200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211,
212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224,
225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237,
238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250};
fitdata1 = Transpose[{time, cases}];
tstart =
First[time];(*selects the first time point from the list of \
days*)tend =
Last[time];(*selects the last time point of the list of \
days*)sol200500 = (inf /.
ParametricNDSolve[{hthy'[t] == -(B/n)*inf[t] hthy[t],
inf'[t] == (B/n)*inf[t] hthy[t] - g*inf[t], rec'[t] == g*inf[t],
hthy[tstart] == n, inf[tstart] == 713,
rec[tstart] == 319197}, {hthy, inf, rec}, {t, tstart, tend}, {B,
g}]);
Then you can run:
bestfit = NonlinearModelFit[fitdata1, sol200500[B, g][t], {{B, 0.1}, {g, 0.1}},t]
Plot[bestfit[t], {t, 200, 250}, Epilog -> Point[fitdata1]]
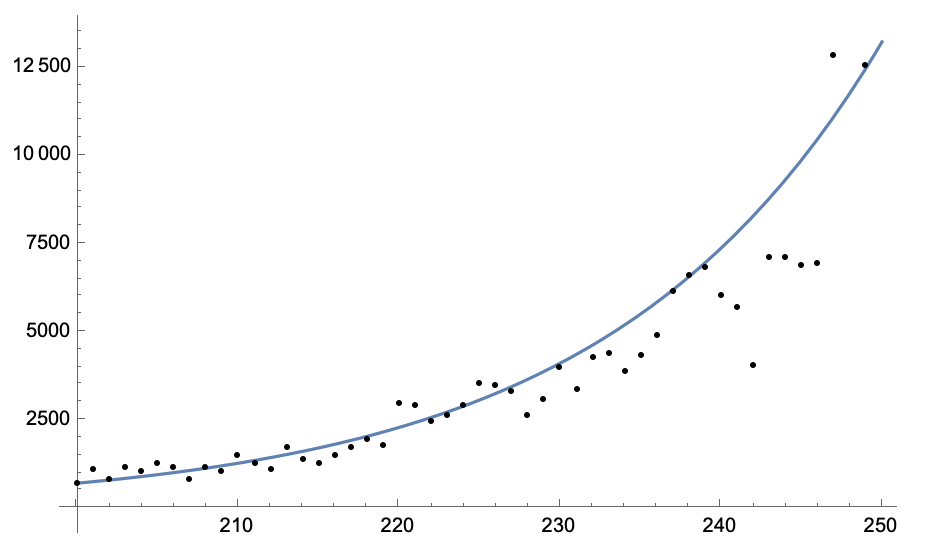
Sorry, haven't had much time to think this through, so you'll need to check this and see whether it makes sense/helps.
Cheers,
Marco