Hi Brad,
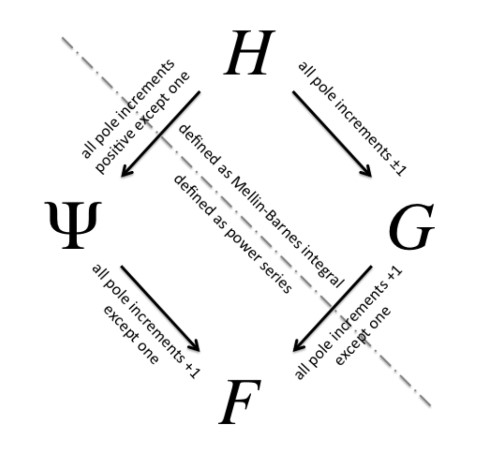
Thanks a lot for your reply. Well, It is correct to say that, in a strict sense, FoxH and Wright's Psi are not hypergeometric functions in general (when any of the real parameters A, B is irrational in your example above). They are in fact "generalizations of" instead of "generalized" hypergeometric functions. However if all parameters A, B, are rationals there is always a p-recurrence and such functions are diferentially finite, being this the case of most applications. For this reason, I think, several researchers (me included), put pFq, MeijerG, Wright's Psi and FoxH functions under the same umbrella: Hypergeometric Functions. For instance this freely available work by Reiner Zorn (2020) "Hypergeometric Functions. Every Thing You Always Wanted to Know About Them (But Were Afraid to Ask)" provides the image below and contains relationships between these 4 functions with some rare FoxH's symbolic expressions and good references to the subject.
Getting back to trinomial equations, (a "simple" and popular application that let us to introduce Fox-Wright function). The starting point is section 4 of the following reference by Müller & Moskowitz (1995), "Reduction of a Class of Fox-Wright Psi Functions for Certain Rational Parameters" Computers Math. Applic. Vol. 30, No. 11, pp. 73-82, 1995, Pergamon.
For positive reals
$x,y$ and
$\alpha>1$ the principal branch of the inverse function of
$y=y(x)$ (sometimes the unique real root
$x$) in
$$x+y x^{\alpha}=1$$ is given by the confluent Fox-Wright function as
$$x=\,_1 \Psi_{1}[(1,\alpha);(2,\alpha -1);-y]$$ a special case of
$\,_p \Psi_q$, the generalized Wright function that can be introduced as follows
$$\,_p \Psi_q [(a_1,A_1),(a_2,A_2)...(a_p,A_p); (b_1,B_1),(b_2,B_2)...(b_q,B_q);\zeta]$$ with
$A_j>0,\; B_k>0,\; j=1,..p,\; k=1,...q,\;$ and
$ \,_p \Psi_q (\zeta)\; $ is given by the series
$$\,_p \Psi_q (\zeta)= \sum_{n=0} ^\infty \frac{\prod_{j=1}^{p}\Gamma(a_j+n\,A_j)}{\prod_{k=1}^{q}\Gamma(b_k+n\,B_k)} \cdot \frac{\zeta^n}{n!}$$
where numerator has no poles for
$n\in\mathbb{N}_0\;$. For
$\kappa=\sum B_k - \sum A_j + 1<0\;$ this series is divergent
$\forall \;\zeta \neq 0$. It converges absolutely and uniformly to an entire function if either
$\kappa>0\;$ or series terminates due to denominator poles for all
$n > m\,$ being
$\,_p \Psi_q (\zeta)\;$ a polynomial of degree
$m\,$. If
$\kappa=0$ it converges with radius of convergence
$\rho=\prod |B_k|^{B_k}/\prod |A_j|^{A_j}\;$ and additionally it converges absolutely on the boundary
$|\zeta|=\rho\;$ if
$\kappa=0\land\Re( \sum a_j - \sum b_k )< \frac{p-q-1}{2}$
The following Mellin-Barnes integral gives a wider representation for
$\,_p \Psi_q (\zeta)\;$
$$\,_p \Psi_q (\zeta) =\frac{1}{2\pi i}\int_{\mathcal{L}}\frac{\Gamma(s)\,\prod_{j=1}^{p}\Gamma(a_j-s\,A_j)}{\prod_{k=1}^{q}\Gamma(b_k-s\,B_k)}(-\zeta)^{-s}\mathcal{d}s$$
provided |arg(
$\zeta\,$)| <
$\pi-\epsilon\,$ with
$\epsilon\,$ > 0 and
$\mathcal{L}\;$ is any of the same three contours of Fox-H function
$\mathcal{L_+}\;$,
$\mathcal{L_-}\;$ and
$\mathcal{L_{i\infty}}\;$ separating the integrand sequence of poles of
$\Gamma(s)\;$ from the rest in this case. For contour
$\mathcal{L_{i\infty}}\;$ the integral converges if
$\epsilon=\frac{\kappa\pi}{2}\;$ and if
$\kappa=0\;$ it provides an analytical continuation of
$\,_p \Psi_q (\zeta)\;$ for
$\zeta\in\mathbb{C}\;$ \ [
$\rho,\infty)$
From this point the connection to Fox-H is evident. In fact
$$\,_p \Psi_q (\zeta) =H_{p,1+q}^{1,p}\,[(1-a_j,A_j)_{j=1}^{p};(0,1),(1-b_k,B_k)_{k=1}^{q};-\zeta\;]$$
$$\,_p \Psi_q (\zeta) =H_{1+q,p}^{p,1}\,[(1,1),(b_k,B_k)_{k=1}^{q};(a_j,A_j)_{j=1}^{p};-\zeta^{-1}\;]$$ where one of these converges and the other is an asymptotic expansion.
From the trinomial solution valid for
$\alpha>1\;$ we have
$$x=H_{1,2}^{1,1}\,[(0,\alpha);(0,1),(-1,\alpha-1);y\;]$$
$$x=H_{2,1}^{1,1}\,[(1,1),(2,\alpha-1);(1,\alpha);y^{-1}\;]$$ For
$0<\alpha<1\;$ and
$\beta=\alpha^{-1}\;$ the trinomial equation can be set as
$$1-x+[(1-x)/y]^{\beta}=1\;$$ giving
$$x=1-H_{1,2}^{1,1}\,[(0,\beta);(0,1),(-1,\beta-1);y^{-\beta}\;]$$
$$x=1-H_{2,1}^{1,1}\,[(1,1),(2,\beta-1);(1,\beta);y^{\beta}\;]$$ Note that if the trinomial equation is set in this form
$$y=c\,x+x^\alpha$$ a variation of such solutions provides the inverse function.
For
$\alpha > 1\;$
$$x=\frac{y}{c}H_{1,2}^{1,1}\,[(0,\alpha);(0,1),(-1,\alpha-1);(y/c)^{\alpha}/y\;]$$
$$x=\frac{y}{c}H_{2,1}^{1,1}\,[(1,1),(2,\alpha-1);(1,\alpha);y(y/c)^{-\alpha}\;]$$ For
$0<\alpha<1\;$ and
$\beta=\alpha^{-1}\;$ the trinomial equation is set as
$$1-\frac{cx}{y}+cy^{\beta-1}(1-\frac{cx}{y})^\beta=1$$ giving
$$x=\frac{y}{c}(1-H_{1,2}^{1,1}\,[(0,\beta);(0,1),(-1,\beta-1);c\,y^{\beta-1}\;])$$
$$x=\frac{y}{c}(1-H_{2,1}^{1,1}\,[(1,1),(2,\beta-1);(1,\beta);y^{-\beta+1}/c\;])$$
From some failed attempts with these formulae it is seen that some basic features of FoxH (in Mathematica v.13) has not been developed. Trinomial equations are very common in scientific practice, it should be very useful to build these direct solutions inside Mathematica (for both symbolics and numerics) now that FoxH functionalities are being expanded.
My Best Regards
Jorge Zuniga
 Attachments:
Attachments: