The above photos show 2D anamorphic images reflecting as 3D objects in a cylindrical mirror. In my previous community contribution, Anamorphosis of 3D-Objects & 3D Printing, I demonstrated the reflection of 3D anamorphic objects to get a realistic 3-dimensional reflection. Identical results can be achieved by reflecting 2D images. I will demonstrate this with two examples: a simple chair built from 132 line segments and a more complicated STL file of a human head consisting of 34,500 triangles obtained from the internet.

1. Chair

We start with a simple model of a chair to test our operating procedure. A chair can be constructed with line segments between a limited number of base points. But since the anamorphic image will transform lines into curves, we will need to interpolate a number of points between the base points.The following function will compute the 3D coordinates of m points evenly distributed between points ptA and ptB.

pointsInLine[{ptA : {xa_, ya_, za_}, ptB : {xb_, yb_, zb_}}, m_] := 
 Transpose[{Subdivide[xa, xb, m], Subdivide[ya, yb, m], 
   Subdivide[za, zb, m]}]

Using the above function, we construct the 3 parts of the chair: seat, sides and back. Since we will later rotate the chair around its vertical axis, we introduce the angle phi as a variable.

seat[phi_] := (pointsInLine[#1, 10] &) /@ 
  Partition[
   RotationTransform[
     phi, {0, 0, 1}, {-2, 0, 0}] /@ {{-2.77`, -0.77`, 1.61}, {-2.77`, 
      0.77`, 1.61}, {-1.23`, 0.77`, 1.61}, {-1.23`, -0.77`, 1.61}}, 2,
    1, {1, 1}]
sides[phi_] :=     
 pointsInLine[#, 10] & /@ 
  Map[RotationTransform[
    phi, {0, 0, 1}, {-2, 0, 
     0}], {{{-2.77`, -0.77`, 0.07}, {-2.77`, -0.77`, 1.61}}, {{-2.77`,
       0.77`, 0.07}, {-2.77`, 0.77`, 1.61}}, {{-1.23`, 0.77`, 
      0.07}, {-1.23`, 0.77`, 1.61}}, {{-1.23`, -0.77`, 
      0.07}, {-1.23`, -0.77`, 1.61}}}, {2}]
back[phi_] :=     
 pointsInLine[#, 10] & /@ 
  Map[RotationTransform[
    phi, {0, 0, 1}, {-2, 0, 
     0}], {{{-2.77`, -0.77`, 3.15`}, {-1.23`, -0.77`, 
      3.15`}}, {{-2.77`, -0.77`, 2.38`}, {-1.23`, -0.77`, 
      2.38`}}, {{-2.77`, -0.77`, 3.15`}, {-2.7`, -0.77`, 
      1.61`}}, {{-1.23`, -0.77`, 3.15`}, {-1.23`, -0.77`, 
      1.61`}}}, {2}]
chair[phi_] := Through[{seat, sides, back}[phi]]

This is the complete chair built from 132 line segments between 12 base points :

With[{phi = -1.25}, 
 Graphics3D[{Red, AbsoluteThickness[8], Line /@ chair[phi]}, 
  Boxed -> False, Axes -> True, AxesOrigin -> {0, 0, 0}]]

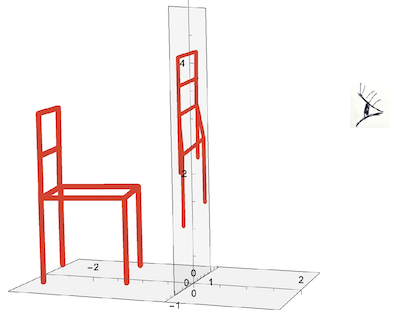
If we look at the chair, we see it as an "observed" 2D image in a plane perpendicular to our view direction. The following functions will convert the 3D chair point by point into a 2D image in the y-z plane if observed from a view point at (xv, 0, zv):

observedPoint[ptR : {xr_, yr_, zr_}, ptV : {xv_, 0, zv_}] := 
 First[NSolveValues[{x, y, z} \[Element] InfiniteLine[{ptR, ptV}] && 
    x == 0, {x, y, z}]]
observedChair[phi_] := 
 Map[observedPoint[#1, {5, 0, 6}] &, chair[phi], {3}]

This code illustrates the relation between the real 3D chair and the observed 2D image:

With[{phi = -1.35}, 
 Graphics3D[{{Opacity[.10], 
    InfinitePlane[{0, 0, 0}, {{0, 1, 0}, {1, 0, 0}}], 
    Polygon[{{0, -1, 0}, {0, -1, 5}, {0, 1, 5}, {0, 1, 0}}]}, {Red, 
    AbsoluteThickness[6], Line /@ chair[phi]}, {Red, 
    AbsoluteThickness[4], Map[Line, observedChair[phi], {2}]}}, 
  Boxed -> False, Axes -> True, AxesOrigin -> {0, 0, 0}]]

The observed image can also be the reflection of an anamorphic 2D image in the x-y plane. To get the anamorphic image of the observed chair, we take the function explained and used here

anamorphPointCF = 
  Compile[{{ptP, _Real, 1}, {ptV, _Real, 1}}, 
   Module[{yi, zi, xv, zv, t1, t2, t3},
    {yi, zi} = ptP;
    {xv, zv} = ptV; t1 = Sqrt[2 + 1/xv^2 + yi^2 - xv^2 (-1 + yi^2)]; 
    t2 = 2 + yi^2 + 1/xv^2 + xv^2; 
    t3 = (1 + 2 xv^2 + yi^2 xv^2 + xv^4); {(-t1/xv + xv (t1 + yi^2))/
       t2 - (-1 + 
         xv^2 (-1 + xv^2 + 
            xv^4 + (-1 - 2 xv^4 + xv^2 (3 + 2 t1)) yi^2)) (zi - (-1 + 
             1/xv^2 + t1 + yi^2) (-zv + zi)/t2)/(xv t3 (-zv + zi)), 
     yi (xv^2 (-1 + xv^2 - t1) t3 + (-1 - xv^2 (2 + 2 t1 + yi^2) + 
            xv^4 (-1 + 2 t1 + 2 yi^2)) (zv + 
             xv^2 zv (-1 + t1 + yi^2) + xv^2 (3 + xv^2 - t1) zi)/(zv -
              zi))/t3^2, 0}], CompilationTarget -> "C"];

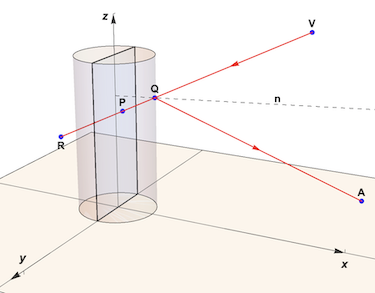
A point R is observed as point P in the y-z plane and is reflected as point A in the x-y plane. The anamorphic point A will be reflected in a cylindrical mirror as P if observed from the view point V at (xv, o, zv)

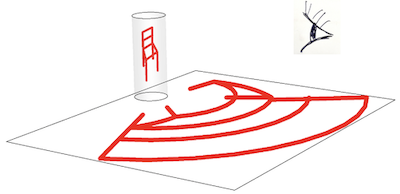
Applied to all 132 points of the chair, we get the chair's anamorphic image. When reflected in the cylindrical mirror, it will appear as the observed chair in the y-z plane.

anamorphChair[phi_] := 
 Module[{xv = 5, zv = 6}, 
  Map[anamorphPointCF[Rest@#, {xv, zv}] &, observedChair[phi], {3}]]
With[{phi = -1.25}, 
 Graphics3D[{{Opacity[.15], Cylinder[{{0, 0, 0}, {0, 0, 5}}, 1], 
    InfinitePlane[{0, 0, -.001}, {{0, 1, 0}, {1, 0, 0}}]}, {Red, 
    AbsoluteThickness[4], Map[Line, anamorphChair[phi], {2}]}, {Red, 
    AbsoluteThickness[2], Map[Line, observedChair[phi], {2}]}}, 
  Lighting -> "Neutral", Boxed -> False]]

For esthetic purposes, we fill the seat polygon. We can now make an animation of the reflected rotating chair:

Animate[Graphics3D[{{Opacity[.15], 
    Cylinder[{{0, 0, 0}, {0, 0, 5}}, 1], 
    InfinitePlane[{0, 0, -.001}, {{0, 1, 0}, {1, 0, 0}}], 
    Polygon[{{-.01, -1, 0}, {-.01, -1, 5}, {-.01, 1, 5}, {-.01, 1, 
       0}}]}, {Red, AbsoluteThickness[5], 
    Map[Line, 
     anamorphChair[phi], {2}], {FaceForm[Lighter[Red, .5]]}, {Red, 
     AbsoluteThickness[2.5], Map[Line, observedChair[phi], {2}]}}}, 
  PlotRange -> {{-1, 14}, {-11, 11}, {-.01, 5}}, Boxed -> False, 
  ViewPoint -> {1, -2, .5}, ImageSize -> Large], {phi, 0, 
  2 \[Pi], \[Pi]/25}]

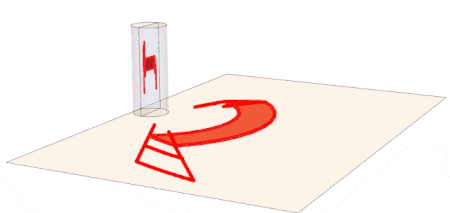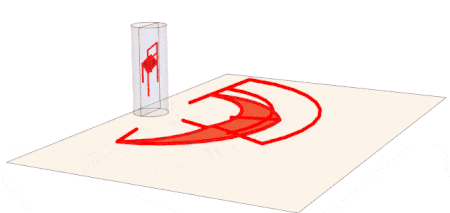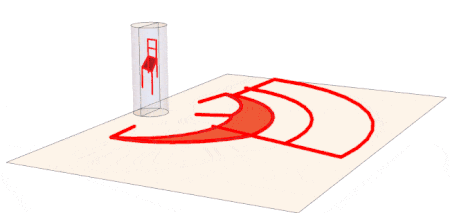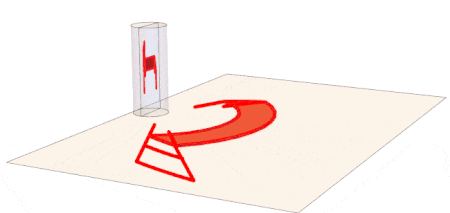
In order to demonstrate this reflected in a real mirror, we use what was previously demonstrated in Introducing Anamorphic Movies: we make a GIF of the rotating anamorphic chair.

iPadFrames = 
  Table[Module[{h = 6, x0 = -2, y0 = 0, z0 = 0, xv = 5, zv = 6, 
     sc = .5, chair, observedChair, anaChair, anaSeat, observedSeat}, 
    ptV = {xv, 0, zv};
    chair = Line[#[phi, sc, {x0, y0, z0}]] & /@ {seat, sides, back};
    observedChair = 
     ParallelMap[observedPoint[#, {xv, 0, zv}] &, chair, {4}];
    anaChair = 
     Map[anamorphPointCF[Rest@#, {xv, zv}] &, observedChair, {4}];
    anaSeat = Polygon[Flatten[anaChair[[1, 1]], 1]]; 
    observedSeat = Polygon[Flatten[observedChair[[1, 1]], 1]];
    Graphics3D[{{Opacity[.15], 
       Polygon[{{0, -1, 0}, {0, -1, h}, {0, 1, h}, {0, 1, 0}}], , 
       InfinitePlane[{0, 0, -.001}, {{0, 1, 0}, {1, 0, 0}}], 
       Cylinder[{{0, 0, 0}, {0, 0, h}}, 1]}, {AbsoluteThickness[8], 
       Red, anaChair}, {FaceForm[Lighter[Red, .5]], anaSeat}}, 
     Axes -> {True, True, False}, AxesStyle -> Gray, Ticks -> None, 
     AxesOrigin -> {0, 0, 0}, Boxed -> False, 
     PlotRange -> {{-4, 17}, {-15, 15}, {-.001, 6}}, 
     ImageSize -> Large, ViewPoint -> {0, 0, 10}]], {phi, 0, 
    2 \[Pi], \[Pi]/20}];
Export[NotebookDirectory[] <> "chair iPad.gif", iPadFrames, 
  AnimationRepetitions -> \[Infinity]];

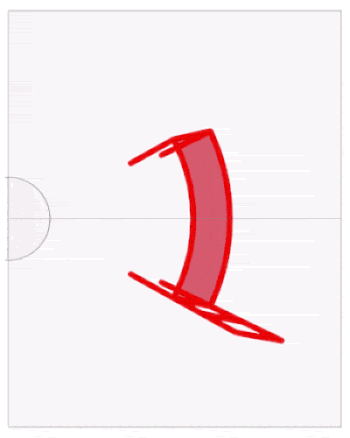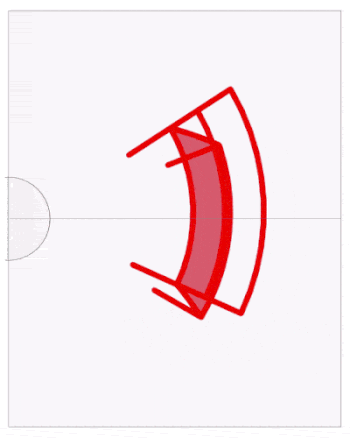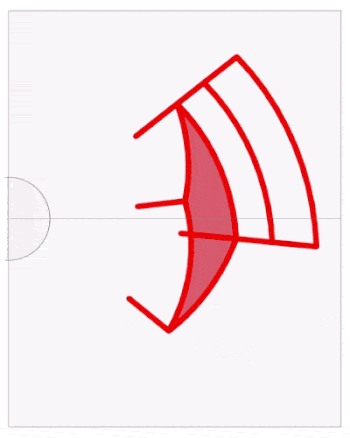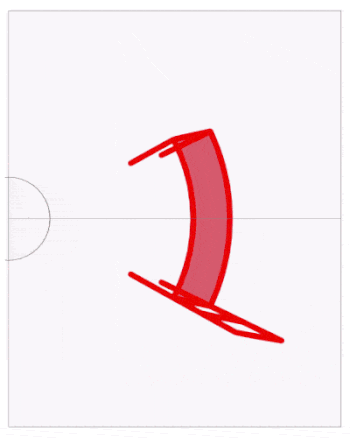
We now upload the (attached)"chair iPad.gif" to an iPad and put a home made cylindrical mirror on top.

This is the result of the GIF's reflection:

2. Human head

We now move to a more complicated example using the same procedure as above. We import an STL file of a human head from: 3D Model Marketplace CGTrader:

headPolys = 
  Import["/Users/er/Downloads/male face 1.stl", "PolygonObjects"];
Length[headPolys[[1]]](*34496*)

Unlike the chair which is "see-through", the head is an opaque sphere and only part of it is visible from any viewpoint. We write a function that will delete the triangles that are invisible if observed from the eye position. Simplified: these are the triangles whose vertices are farther away from vie point V at (xv, 0, zv) than a certain distance d. This way, we extract the 25,600 visible triangles out of the the total amount of 34,496

Quiet[Module[{d = .05, scalingDivider = 20, x0 = -.5, z0 = 1.75, 
   xv = 10, zv = 5, rawScaledVertices, scaledVertices, 
   visibleVertices, observedVertices}, 
  rawScaledVertices = 
   RotationTransform[Pi/2, {0, 0, 1}] /@ 
     headPolys[[1]] /. {x_?NumericQ, y_, z_} -> {x, y, z}/
      scalingDivider;
  visibleVertices = 
   Length[
    DeleteCases[
     scaledVertices, _?(findInvisibles[#1, d] == True &)]];
  observedVertices = 
   ParallelMap[observedPoint[#1, {xv, 0, zv}] &, visibleVertices, {2}];
  Row[(Graphics3D[{FaceForm[LightGray], 
        EdgeForm[AbsoluteThickness[.1]], Triangle[#1]}, 
       Boxed -> False, ViewPoint -> Front, 
       Lighting -> "Accent"] &) /@ {scaledVertices, visibleVertices, 
     observedVertices}]]]

Above left, we see the complete head with all triangles. In the middle is a side view of only the visible triangles. At right are the visible triangles as observed from the view point. We now compute the anamorphic map of the visible triangles:

Quiet@Module[{d = .12, scalingDivider = 22,(*offset*)x0 = -.5, 
   z0 = 1.75, xv = 10, zv = 5, rawScaledVertices, scaledVertices, 
   visibleVertices, observedVertices, anamorphVertices},
  rawScaledVertices = 
   RotationTransform[.4, {0, 0, 1}] /@ 
     headPolys[[1]] /. {x_?NumericQ, y_, z_} -> {x, y, z}/
      scalingDivider;
  scaledVertices = 
   DeleteCases[rawScaledVertices, _?(findInvisibles[#, d] &)];
  visibleVertices = 
   DeleteCases[
    scaledVertices, _?(polyCheck[#, {x0, 0, z0}, {xv, 0, zv}] == 
        3 &(*all 3 vertices under view plane*))];
  observedVertices = 
   ParallelMap[observedPoint[#, {xv, 0, zv}] &, visibleVertices, {2}];
   anamorphVertices = 
   ParallelMap[anamorphPointCF[Rest@#, {xv, zv}] &, 
    observedVertices, {2}];
  Graphics[{{FaceForm[Lighter[Gray, .5]], 
     EdgeForm[AbsoluteThickness[.1]], 
     Polygon[
      anamorphVertices /. {x_?NumberQ, y_, z_} -> {x, y}]}, {Dashed, 
     Circle[]}}, PlotRange -> {{-5, 12}, {-10, 10}}, 
   ImageSize -> 250]]

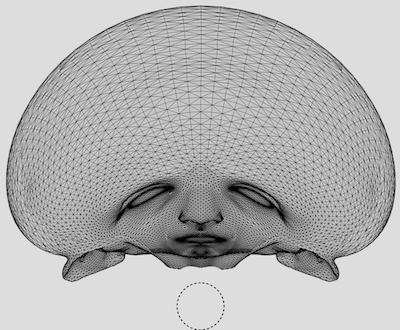
Reflected in the mirror, the anamorphic image is observed as the complete 3D head:

As we did with the chair, we animate the anamorphic image by varying the rotation angle around a vertical axis.

With[{d = .12, scalingDivider = 24,(*offset*)x0 = -.5, z0 = 1.75, 
   xv = 10, zv = 5}, 
  headFrames = 
   Table[
    Module[{rawScaledVertices, scaledVertices, visibleVertices, 
      observedVertices, anamorphVertices},
     rawScaledVertices = 
      RotationTransform[phi, {0, 0, 1}] /@ 
        headPolys[[1]] /. {x_?NumericQ, y_, z_} -> {x, y, z}/
         scalingDivider;
     scaledVertices = 
      DeleteCases[rawScaledVertices, _?(findInvisibles[#, d] &)];
     visibleVertices = 
      DeleteCases[
       scaledVertices, _?(polyCheck[#, {x0, 0, z0}, {xv, 0, zv}] == 
           3 &(*all 3 vertices under view plane*))];
     observedVertices = 
      ParallelMap[observedPoint[#, {xv, 0, zv}] &, 
       visibleVertices, {2}]; 
     anamorphVertices = 
      ParallelMap[anamorphPointCF[Rest@#, {xv, zv}] &, 
       observedVertices, {2}];
     Graphics[{{FaceForm[Lighter[Gray, .5]], 
        EdgeForm[AbsoluteThickness[.1]], 
        Polygon[
         anamorphVertices /. {x_?NumberQ, y_, z_} -> {x, 
            y}]}, {Dashed, Circle[]}}, 
      PlotRange -> {{-5, 12}, {-10, 10}}, ImageSize -> 600]], {phi, 0,
      2 \[Pi] - \[Pi]/30, \[Pi]/30}]];
Export[NotebookDirectory[] <> "head iPad.gif", headFrames, 
 AnimationRepetitions -> \[Infinity]]

We load the GIF to an iPad and see its reflection in a cylindrical mirror. The reflection appears as a virtual image of a 3D rotating head inside the cylinder. I attached the two GIF files "chair iPad.GIF" and "head iPad.GIF". Load them to your iPad and see the magic! Have fun!

Attachments:

char iPad.gif

head iPad.gif