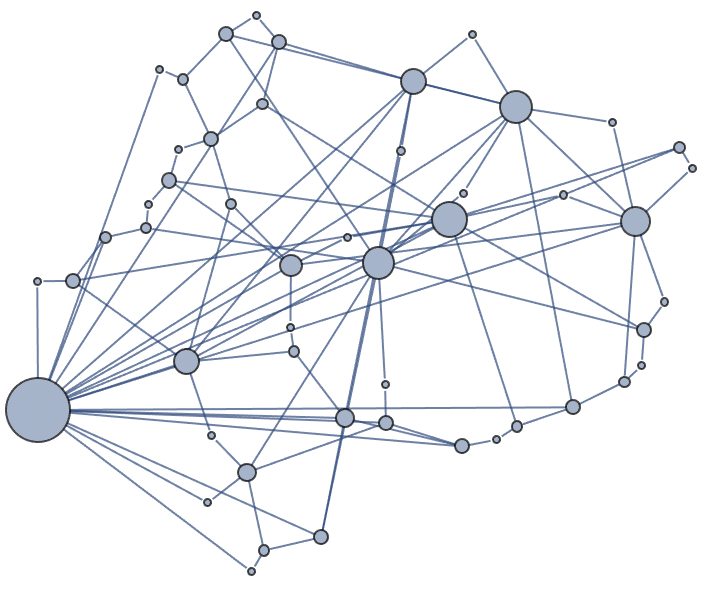
You did not elaborate on what exactly you want to show by using vertex weights in the graph layout, so I will go with the following:

• Let high-weight vertices repulse other vertices. This creates space around them for drawing them in a larger size, as well as for drawing more vertices around them (if they happen to have a high degree as well).
• Let us also render high-weight vertices in a larger size.

The following implementation uses IGraph/M.

Let us first create a graph with heterogeneous degrees, and record the degrees as vertex weights.

SeedRandom[123];
g = IGBarabasiAlbertGame[50, 2, DirectedEdges -> False]

Instead of VertexDegree, I will use IGVertexStrength. If you have a graph with edge weights, this would use the weighted degree (sum of incident edge weights).

g = g // IGVertexMap[# &, VertexWeight -> IGVertexStrength];

To achieve our goal, we will use a layout method that takes edge weights into account. Here I use IGLayoutFruchtermanReingold, which draws shorter edges for higher edge weights. Thus, we can set the weight of an edge to be the produce of the weights of its endpoint vertices, and finally transform it as $1/ w^\alpha$ to make large weights out of small ones. $\alpha$ serves to tune the repulsion.

alpha = 1.5; (* tunes repulsion of high-weight vertices *)
beta = 1; (* tunes vertex size based on vertex weight *)
g //
  IGEdgeMap[Apply[Times], EdgeWeight -> IGEdgeVertexProp[VertexWeight]] // (* convert vertex weight to edge weight *)
  IGEdgeMap[1/#^alpha &, EdgeWeight] // (* transform large edge weight to small *)
  IGVertexMap[0.1 #^beta &, VertexSize -> IGVertexProp[VertexWeight]] // (* set vertex size based on vertex weight *)
  IGLayoutFruchtermanReingold (* do the layout *)

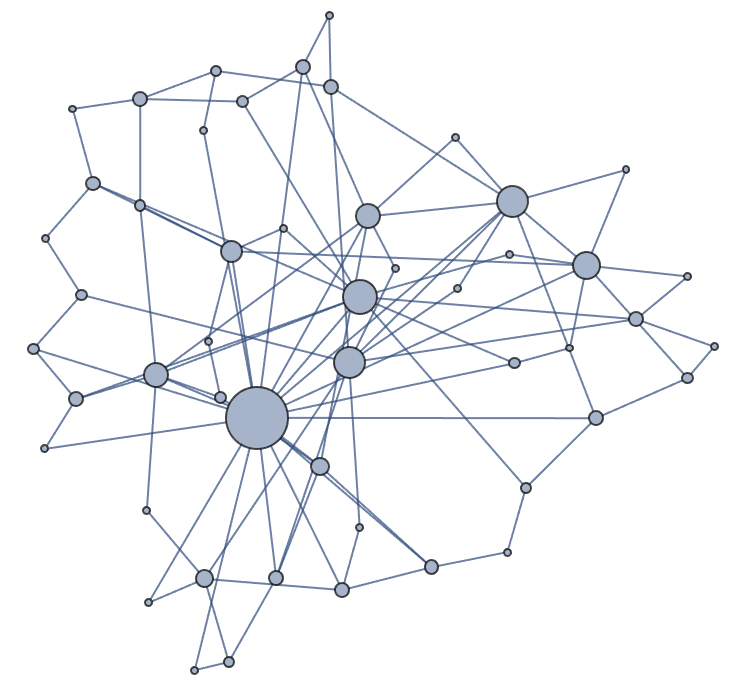
IGLayoutFruchtermanReingold is similar to Mathematica's built-in "SpringElectricalEmbedding". You can also turn on edge-weight support in that layout method.

IGLayoutKamadaKawai could also be used. It is similar to "SpringEmbedding" and generally does a good job of drawing edges at a length that follows their weight. However, I found that this method will push high-weight vertices to the periphery. While that is natural (they are repulsive), this is not an intuitive graph visualization. We want high-weight vertices to stay in the middle. As example, it might produce a layout like the following (not desirable):