In another recent thread on tiling games, we ended up giving some statistics that make the system function SatisfiabilityInstances look slow. While cover problems are good enough to do just about anything in tiling, it might be the case that other methods of tiling have different performance statistics. Even though Wang tiles are not covered in NKS, we still have to take them seriously because of Wang's conjecture, and recent progress finding minimal results. The purpose of this memo is to give updated tile solvers and show how to go from Wang tiles to block templates in the special case of the Jeandel-Rao tiling.

Here is what I did today to celebrate Juneteenth (again), since we have a nice "free" Monday, here at Wolfram Research:

GenerateWangTiling[patterns_, init_, size_Integer, rest___] := 
  GenerateWangTiling[patterns, init, {size, size}, rest];

GenerateWangTiling[{}, ___] := Failure["NotTileable", <||>];

GenerateWangTiling[
  patterns : {{(_Integer | Verbatim[_]) ...} ...},
                 init : {(_Integer | Verbatim[_]) ...} ,
                 size : {_Integer, _Integer},
                 count : (Integer | Automatic | All) : Automatic,
                 opts : OptionsPattern[{"Boundary" -> "Any"}]]  := 
 Module[{
   bitLen = BitLength[Max[Cases[patterns, _?NumberQ, Infinity]]],
   initXY = Map[ #@Ceiling[(size ) / 2] &, {First, Last}],
   squaresArray = Reverse@Table[Sort[
         UndirectedEdge[#1, #2]
         ] & @@@ Partition[{j, i} + # & /@ {
          {0, 0}, {1, 0}, {1, 1}, {0, 1}},
        2, 1, 1], {i, size[[1]]}, {j, size[[2]]}],
   varsRep, vars, initLogic, edgeLogic, boundLogic, matSolved},
  varsRep = MapIndexed[Rule[#1,
      Function[{ind}, edge[#2[[1]], ind]] /@ Range[bitLen]
      ] &, Union[Flatten[squaresArray]]];
  squaresArray = squaresArray /. varsRep;
  initLogic = If[Length[init] == 4, And @@ Flatten[MapThread[
       Switch[#2, 1, Identity, 0, Not]@#1 &,
       {squaresArray[[Sequence @@ initXY]],
        IntegerDigits[#, 2, bitLen] & /@ init}, 2]], True];
  vars = Union[Flatten[varsRep[[All, 2]]]];
  edgeLogic = Apply[And, Or @@@ Outer[
      And @@ (And @@ # & /@
          MapThread[Switch[#2, 0, Not[#1], 1, #1] &,
           {#1, IntegerDigits[#2, 2, bitLen]}, 2]) &,
      Flatten[squaresArray, 1],
      patterns, 1]];
  boundLogic = Switch[OptionValue["Boundary"],
    "Any", True,
    "Periodic", And[
     And @@ Flatten[Table[
        Or[
         squaresArray[[i, 1, 4, k]] && 
          squaresArray[[i, size[[2]], 2, k ]] ,
         ! squaresArray[[i, 1, 4, k]] && ! 
           squaresArray[[i, size[[2]], 2, k ]]],
        {i, 1, size[[1]] }, {k, 1, bitLen}], 1] ,
     And @@ Flatten[Table[
        Or[
         squaresArray[[1, j, 3, k]] && 
          squaresArray[[ size[[1]], j, 1, k ]] ,
         ! squaresArray[[1, j, 3, k]] && ! 
           squaresArray[[ size[[1]], j, 1, k ]]],
        {j, 1, size[[2]] }, {k, 1, bitLen}], 1]]];
  matSolved = Map[FromDigits[#, 2] &, squaresArray /. MapThread[Rule,
        {vars, 
         Association[{True -> 1, False -> 0}][#] & /@ #}], {3}] & /@
    SatisfiabilityInstances[And[initLogic, edgeLogic, boundLogic],
     vars, Replace[count, Automatic -> 1], Method -> "SAT"];
  If[SameQ[matSolved, {}], 
   Return[Failure["NotTileable", <||>], Module]];
  If[SameQ[count, Automatic], First, Identity][matSolved]]

It's similar to GenerateTiling, but more robust and faster, as we shall see shortly. First let's do a simple test on periodic input to see how well this new function works:

WangTile[or_, tile_, colRules_ :
   {0 -> White, 1 -> Red, 2 -> Blue, 3 -> Green, 4 -> Gray}
  ] := MapThread[
  {#1, EdgeForm[Black], Polygon@Append[or + # & /@ #2, or]} &,
  {tile /. colRules,
   {{{-1/2, -1/2}, {1/2, -1/2}},
    {{1/2, -1/2}, {1/2, 1/2}},
    {{1/2, 1/2}, {-1/2, 1/2}},
    {{-1/2, 1/2}, {-1/2, -1/2}}}}, 1]  

Show@MapIndexed[Graphics@WangTile[
       Reverse[#2 {-1, 1}], #1] &,
    #, {2}] & /@ GenerateWangTiling[{
   {1, 3, 2, 4}, {2, 4, 1, 3}}, {}, 4, All,
  "Boundary" -> "Periodic"]

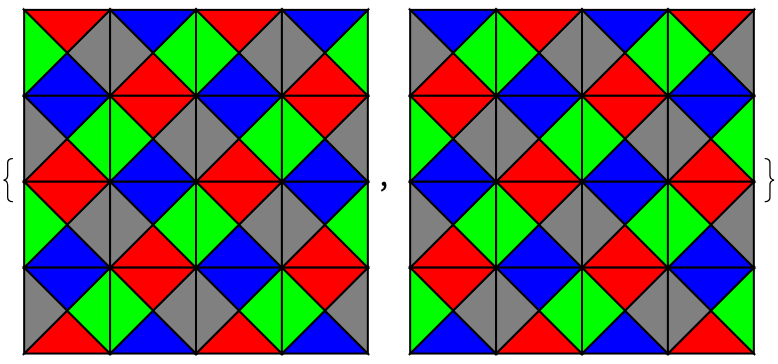
If the second argument is set to either {1,3,2,4} or {2,4,1,3}, we get only one of these patterns. If the third argument is set to either 3 or 5 we get nothing because the boundary condition can't be met.

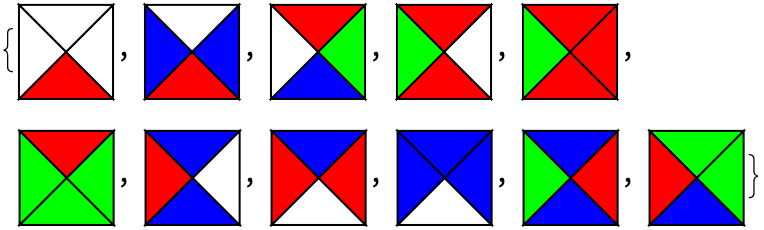
Now let's introduce the Jeandel-Rao tiles (Coped from mathworld, thanks Ed!):

JeandelRaoTiles = {
   {1, 0, 0, 0},
   {1, 2, 0, 2},
   {2, 3, 1, 0},
   {1, 0, 1, 3},
   {1, 1, 1, 3},
   {3, 3, 1, 3},
   {2, 0, 2, 1},
   {0, 1, 2, 1},
   {0, 2, 2, 2},
   {2, 1, 2, 3},
   {2, 3, 3, 1}
   };

Graphics[WangTile[
    {0, 0}, #], ImageSize -> 50] & /@ JeandelRaoTiles 

We can get a sense of combinatorics by counting valid $3x3$ arrangements:

Length@GenerateWangTiling[JeandelRaoTiles, #, {3, 3}, All] & /@ JeandelRaoTiles
Total[%] 

Out[]={61, 29, 85, 23, 13, 58, 76, 50, 18, 77, 36}
Out[]=526

For example plotting just one of these:

Show@MapIndexed[Graphics@WangTile[
     Reverse[#2 {-1, 1}], #1] &,
  GenerateWangTiling[JeandelRaoTiles,
   JeandelRaoTiles[[1]], {3, 3}], {2}]

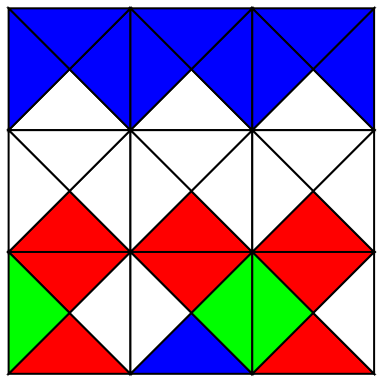
Now we can try and experiment and see if it works. Starting from combinatorially complete atlas of tile surroundings, we will extract four-color, $3x3$ templates (see Chapter 5 of NKS) from the tilted square grid made by matching the Wang tiles. It's not that difficult:

data23 = GenerateWangTiling[JeandelRaoTiles, {}, {2, 3}, All];
data32 = GenerateWangTiling[JeandelRaoTiles, {}, {3, 2}, All];

templates3x3 = Union@Join[
    Union[{{#[[1, 1, 1]], #[[1, 1, 2]], #[[1, 2, 3]]},
        {#[[2, 1, 2]], #[[2, 2, 3]], #[[1, 2, 2]]},
        {#[[2, 2, 1]], #[[2, 2, 2]], #[[2, 3, 3]]}
        } & /@ data23],
    Union[{{#[[2, 1, 4]], #[[2, 1, 3]], #[[1, 1, 2]]},
        {#[[2, 1, 1]], #[[2, 1, 2]], #[[2, 2, 3]]},
        {#[[3, 1, 2]], #[[3, 2, 3]], #[[2, 2, 2]]}
        } & /@ data32]];

and the $2\times 2$ templates can be extracted from $3\times 3$:

templates2x2 = Union[Flatten[Flatten[
      Partition[#, {2, 2}, {1, 1}],
      1] & /@ templates3x3, 1]]

Now we want to compare tilings from templates with the original wang tiling to see if we obtained good results. For this we need an updated version of GenerateTiling, which has some bug fixes and expanded capabilities for dealing with more than two colors:

DisplaceLogic[expr_, {dx_, dy_}] := ReplaceAll[expr,
    {Tile[x_, y_, z_] :> Tile[x + dx, y + dy, z]}];

LocalLogic[patterns : {
     {{(_Integer | Verbatim[_]) ...} ...} ...},
   dims_] := With[{
    variables = Table[Tile[i, j, k],
       {i, 1, dims[[1]]}, {j, 1, dims[[2]]}, {k, 1, dims[[3]]}],
    patternsValues = Map[If[MatchQ[#, Verbatim[_]],
          Array[_ &, {dims[[3]]}], IntegerDigits[#, 2, dims[[3]]]
          ] &, #, {2} ] & /@ patterns},
   Apply[Or, Apply[And, Flatten[MapThread[
         Switch[#1, 1, Identity, 0, Not, Verbatim[_], Nothing
            ][#2] &, {#, variables}, 3]]] & /@ patternsValues]];

EdgesFilter[logic_, {sizex_, sizey_}] := ReplaceAll[
  ReplaceAll[ReplaceAll[logic, {
     Tile[x_ /; Or[x < 1, x > sizex], _, _] :> TE,
     Tile[_, y_ /; Or[y < 1, y > sizey], _] :> TE
     }], Not[TE] -> True], TE -> True]

TilingMatrixResults[rules_] := Map[
  FromDigits[
    SortBy[#, #[[1, 3]] &][[All, 2]] /. {True -> 1, False -> 0}, 
    2] &,
  Map[Values[KeySort[GroupBy[#, #[[1, 2]] &]]] &,
   Values[KeySort[GroupBy[rules, #[[1, 1]] &]]]], {2}]

GenerateTiling[patterns_, init_, size_Integer, rest___] := 
  GenerateTiling[patterns, init, {size, size}, rest];

GenerateTiling[{}, ___] := Failure["NotTileable", <||>];

GenerateTiling[patterns : {{{(_Integer | Verbatim[_]) ...} ...} ...},
  init : {{(_Integer | Verbatim[_]) ...} ...} ,
   size : {_Integer, _Integer}, count_ : Automatic,
  opts : OptionsPattern[{"Boundary" -> "Any"}]
  ]  := Module[{
   dims = Append[Dimensions[patterns[[1]]],
     BitLength[Max[Cases[patterns, _?NumberQ, Infinity]]]],
   initXY = Map[ Subtract[#@Floor[(size ) / 2] ,
       Floor[#@Dimensions[init] / 2]] &, {First, Last}],
    localLogic, initLogic, overlapLogic, boundLogic, vars, 
   solutions},
  initLogic = If[
    And[Length[Dimensions[init]] == 2, UnsameQ[Flatten[init], {}]],
     DisplaceLogic[
     LocalLogic[{init}, Append[Dimensions@init, dims[[3]] ]], initXY],
     True];
  vars = 
   Flatten @ 
    Table[Tile[i, j, k], {i, size[[1]] }, {j, size[[2]] }, {k, 
      dims[[3]]}];
  localLogic = LocalLogic[patterns, dims];
  overlapLogic = EdgesFilter[ And @@ Catenate @ Table[
       DisplaceLogic[localLogic, {i, j}],
       {i, -dims[[1]], size[[1]]}, {j, -dims[[2]], size[[2]]}], 
    size];
  boundLogic = Switch[OptionValue["Boundary"],
    "Any", True,
    "Periodic", And[
     And @@ Flatten[Table[
        Or[Tile[i, 1, k] && Tile[i, size[[2]], k ] ,
         ! Tile[i, 1, k] && ! Tile[i, size[[2]], k ]],
        {i, 1, size[[1]] }, {k, 1, dims[[3]]}], 1] ,
     And @@ Flatten[Table[
        Or[Tile[1, j, k] && Tile[ size[[1]], j, k ] ,
         ! Tile[1, j, k] && ! Tile[ size[[1]], j, k ]],
        {j, 1, size[[2]] }, {k, 1, dims[[3]]}], 1]]];
  solutions = SatisfiabilityInstances[And[
     initLogic , overlapLogic , boundLogic],
    vars, Replace[count, Automatic -> 1], Method -> "SAT"];
  If[solutions === {}, Return[Failure["NotTileable", <||>], Module]];
  If[count === Automatic, First, Identity][
   TilingMatrixResults[MapThread[Rule, {vars, #}]] & /@
          solutions]]

Here's a basic timing test comparing two algorithms:

AbsoluteTiming[
 Show@MapIndexed[Graphics@WangTile[
      Reverse[#2 {-1, 1}], #1] &,
   GenerateWangTiling[JeandelRaoTiles, {}, 20], {2}]
 ]

AbsoluteTiming[
 ArrayPlot[GenerateTiling[templates3x3, {}, 20], ColorRules -> {
    0 -> White, 1 -> Red, 2 -> Blue,
     3 -> Green, 4 -> Gray}, Mesh -> True]
 ]

The experiment seems to work, albeit with a slower time using templates. Even though the template result looks okay, upon closer scrutiny it turns out to be a False positive. Just try deleting every template with a green value, then:

AbsoluteTiming[
 ArrayPlot[GenerateTiling[Select[templates3x3,
    ! MemberQ[Flatten[#], 3] &], {}, 20], ColorRules -> {
    0 -> White, 1 -> Red, 2 -> Blue,
     3 -> Green, 4 -> Gray}, Mesh -> True]] 

If a subset allows a periodic tiling, the superset must as well, so our initial attempt at constructing template must have failed. The important thing to realize is that, in the call above, we are not looking at all possible tilings, so might have been fooled.

Back to the drawing board, or better, to notes from Ed Pegg (who happens to be an expert on aperiodic tilings). Notice that the $2 \times 2$ templates include the original Wang tiles:

SubsetQ[templates2x2,
 {{#[[4]], #[[3]]}, {#[[1]], #[[2]]}} & /@ JeandelRaoTiles]
 Out[] = True

These templates are centered on one particular sublattice of $\mathbb{Z}^2$, and if we distinguish them as being so, we should get a set of templates equivalent to the original wang tiling. To do this, we will add symbols $4$ and $5$ denoting alternative sublattices

data22 = GenerateWangTiling[JeandelRaoTiles, {}, {2, 2}, All];
data33 = GenerateWangTiling[JeandelRaoTiles, {}, {3, 3}, All];
center2x2 = Union[{{#[[2, 2, 4]], #[[2, 2, 3]]},
      {#[[2, 2, 1]], #[[2, 2, 2]]}} & /@ data33];
offCenter2x2 = Union[{{#[[1, 1, 1]], #[[1, 1, 2]]},
      {#[[2, 1, 2]], #[[2, 2, 3]]}} & /@ data22];

vonNeumannTemplates = Join[center2x2 /. {
     {{c4_, c3_},
       {c1_, c2_}} :> {
       {_, c3, _},
       {c4, 4, c2},
       {_, c1, _}}},
   offCenter2x2 /. {
     {{c4_, c3_},
       {c1_, c2_}} :> {
       {_, c3, _},
       {c4, 5, c2},
       {_, c1, _}}},
   Flatten[Table[
     {{{_, 4, _}, {5, a, 5}, {_, 4, _}},
      {{_, 5, _}, {4, a, 4}, {_, 5, _}}},
     {a, 0, 3}], 1]];

Length@vonNeumannTemplates
Out[] = 48

And notice $8$ extra templates have been added in to help with lining up the sublattices (again, thanks Ed!). Now let's take this set of templates and check to see if the delete-the-green trick yields a periodic tiling:

GenerateTiling[Select[vonNeumannTemplates,
  ! MemberQ[Flatten[#], 3] &], {}, 20]
Out[]= "Failure not tileable".

This isn't a proof, but gives us some confidence that we haven't made a coding error. I think the correctness proof is really straightforward, but we will not go over it here. Instead, let's just look at the plot leaving in the greens:

AbsoluteTiming[
 data = GenerateTiling[vonNeumannTemplates, {}, 20];]
Out[] = 2 seconds

ArrayPlot[data,
 ColorRules -> {0 -> White, 1 -> Red, 2 -> Blue, 3 -> Green, 
   4 -> Gray, 5 -> Black}]

But this does not look exactly as we expect due to Black and Gray squares. Just imagine WRGB colors seeping across adjacencies, or even better, transform out the Gray and Black squares:

Graphics[With[{JRtiling = GenerateTiling[vonNeumannTemplates, {}, 20]},
  MapThread[{#2, 
     Rectangle /@ #1} &, {Map[RotationMatrix[-Pi/4] . #/Sqrt[2] &, 
       Position[JRtiling, #]
       ] & /@ {0, 1, 2, 3}, {White, Red, Blue, Green}}]]]

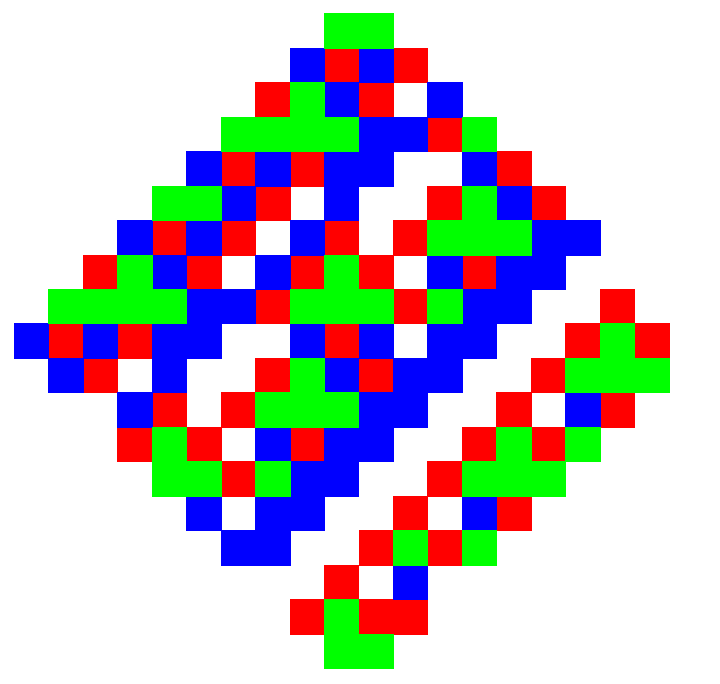
Unfortunately we get a smaller patch of the tiling after a longer wait, so it is not clear what we've gained (other than perhaps some new insight) by changing to template. Anyways it takes about 16 seconds to calculate an even larger patch:

We've now seen that the SAT solver can go decently fast when directly calculating colors of a Wang tiling directly on Edges. Referring back to the previous thread, how does the wang SAT time compare to an approach using Exact Cover? All that we need to do is change edge matching rules into an exact cover matrix. Any summer school students interested to try this problem?