Group Abstract Group Abstract

Message Boards Message Boards

A simple quadratic equation cannot be solved?

Werner Geiger
Posted 3 years ago

Of course a trivial quadratic equation can be solved by Solve: 

eqn = a1 + b1*x + c1*x^2;
cl = CoefficientList[eqn, x];
{time, sol} = AbsoluteTiming[Solve[eqn == 0, x, Reals]];
Echo[Column[{eqn, Column[cl, Frame -> Thin], sol, time}, Frame -> True]];

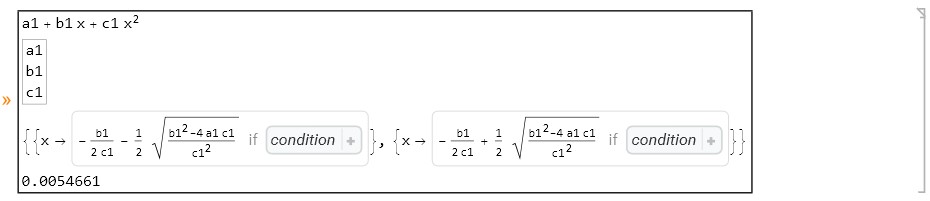
enter image description here

If you use some more complicated coefficients, the equation is still solved but takes pretty long (about 13 seconds on my machine). For me it's not understandable why it takes significantly longer. It's still a trivial quadratic equation. I assume the time is spent during simplification of the conditions.

eqn = (-4 + c1^2 + 2 c1*c2 + c2^2 + (s1 + s2)^2)/4 - 
   3/8*(a2*r1 + a1*r2)*(c2*s1 - c1*s2)*x + 
   9/64*(a1^2*r2^2*(c1^2 + s1^2) - 2*a1*a2*r1*r2 )*x^2;
cl = CoefficientList[eqn, x];
{time, sol} = AbsoluteTiming[Solve[eqn == 0, x, Reals]];
Echo[Column[{eqn, Column[cl, Frame -> Thin], sol, time}, Frame -> True]];

enter image description here

When you make a coefficient even more complicated (here an additional term (c1c2+s1s2) within the x^2-coefficient), Solve does not come to an end. At least not after two minutes on my machine. You have to abort the evaluation by Alt+"." or surround it by TimeConstrained.

eqn = (-4 + c1^2 + 2 c1*c2 + c2^2 + (s1 + s2)^2)/4 - 
   3/8*(a2*r1 + a1*r2)*(c2*s1 - c1*s2)*x + 
   9/64*(a1^2*r2^2*(c1^2 + s1^2) - 2*a1*a2*r1*r2 (c1*c2 + s1*s2))*x^2;
cl = CoefficientList[eqn, x];
{time, sol} = AbsoluteTiming[Solve[eqn == 0, x, Reals]];
Echo[Column[{eqn, Column[cl, Frame -> Thin], sol, time}, Frame -> True]];
(* .... $Aborted ...*)

Does anyone have an explanation for this strange behavior? And how to overcome it?

I've managed it by partially replacing the coefficients with new variables and then examining and interpreting the conditions myself. But this is quite involved and of course very specific to the concrete equation.

POSTED BY: Werner Geiger
6 Replies
Sort By:

Even in the complex case the full solution can be pretty complicated, if you ask for the full solvability conditions;

eqn = (-4 + c1^2 + 2 c1*c2 + c2^2 + (s1 + s2)^2)/4 - 
   3/8*(a2*r1 + a1*r2)*(c2*s1 - c1*s2)*x + 
   9/64*(a1^2*r2^2*(c1^2 + s1^2) - 2*a1*a2*r1*r2)*x^2;
Echo[Reduce[eqn == 0, x]];

In the real case, the solvability conditions involve analyzing a semialgebraic variety of high degree in several variables.

It is true that when the generated conditions are too complicated they are hard to use in practice. Would you like Mathematica to return simply

Echo[Discriminant[eqn, x] >= 0];

as the condition for real solutions?
POSTED BY: Gianluca Gorni
Werner Geiger
Werner Geiger
Posted 3 years ago

I know, Gianluca. I prefer Echo since it makes the code and the output more readable. And since I can easily disable it globally by:

$ContextPath = Prepend[$ContextPath, "myContext`"];
Echo[any___] := Null;

Actually I use my own echo-function with takes a global variable testLvl that controls which Echo-output shall be produced.
POSTED BY: Werner Geiger

Solving over the complexes is easier because algebra and analysis are in some sense complete. In your case, an algebraic equation is to be solved, and it helps that the complexes is an algebraically closed field. To solve over the Reals, Mathematica solves for the conditions on the other variables/parameters that specify exactly when the quadratic formula gives real solutions. There's a fast way to do that, but Mathematica probably tries to reduce the condition (perhaps via Reduce or one of its subfunctions). That's probably what takes so long.
POSTED BY: Michael Rogers

I noticed that you use the construct

Echo[something];

I think you can save some typing with a simple

something

without the semicolon.

The semicolon suppresses the output, and Echo undoes the suppression. My suggestion is to suppress both semicolon and Echo.
POSTED BY: Gianluca Gorni
Werner Geiger
Werner Geiger
Posted 3 years ago

This works indeed, Mariusz (within 0,06 secs). But why? I had never thought that solving in Complex would be easier than within Reals. But anyway this is a valid solution. I can apply the Reals-condition later to the result.
POSTED BY: Werner Geiger

A dirty workaround is:

  Solve[eqn == 0, x]

without Reals in Solve.
POSTED BY: Mariusz Iwaniuk
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard