@Peter Burbery it's the hand-waving, the development of the Mixed Chinese Postman Problem, that gets us the optimum tour for a mixed graph.
PacletInstall["PeterBurbery/MixedGraphs"];
%["Location"];
PacletDirectoryLoad[
"/Users/deangladish/mixed-graphs-paclet/Mixed Graphs"];
PacletInstall[
"/Users/deangladish/mixed-graphs-paclet/Mixed \
Graphs/build/PeterBurbery__MixedGraphs-1.21.0.paclet"];
PacletFind["PeterBurbery/MixedGraphs"]
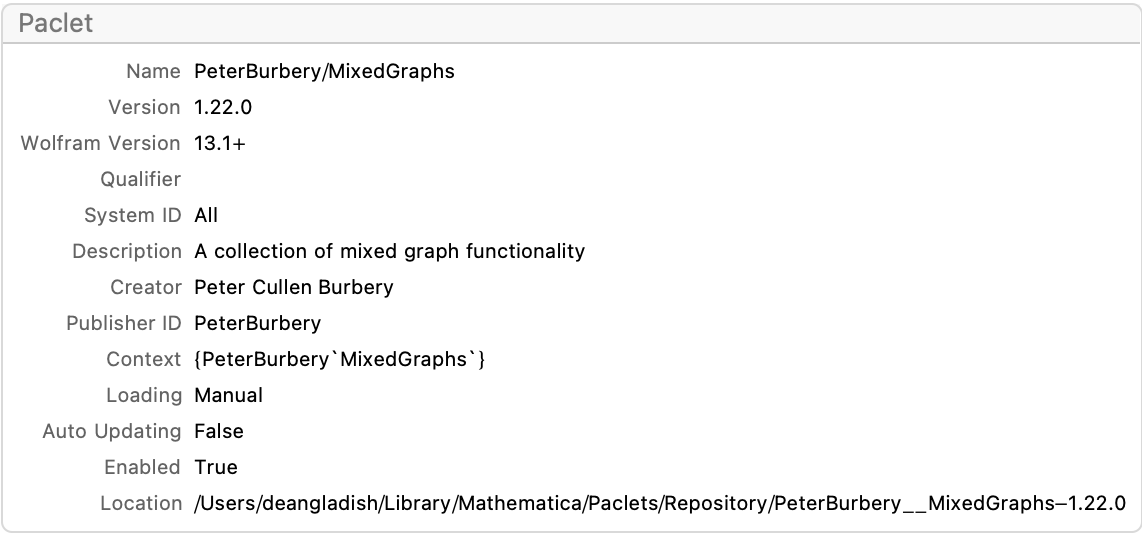
Information[PacletObject["PeterBurbery/MixedGraphs"]]
$ContextPath;
Directory[];


And then your GitHub, the MixedGraphs that allows us to get so many versions on ~/mixed-graphs-paclet/ and in Mixed Graphs/build, and there are so many .nbs in the directory, Peter, we can get them directly.
Get["/Users/deangladish/mixed-graphs-paclet/Mixed \
Graphs/build/PeterBurbery__MixedGraphs/Kernel/MixedGraphs.wl"]
Differentiating between Version 1.22.0 and 1.21.0.
Animate[Module[{g},
g = RandomGraph[BernoulliGraphDistribution[20, p], ImageSize -> 300];
g = First[TakeLargestGraphComponentBy[g]];
g = EulerizeGraph[g];
HighlightGraph[g, Subgraph[g, RandomSample[VertexList[g], 3]]]], {p,
0.1, 1, 0.1}]
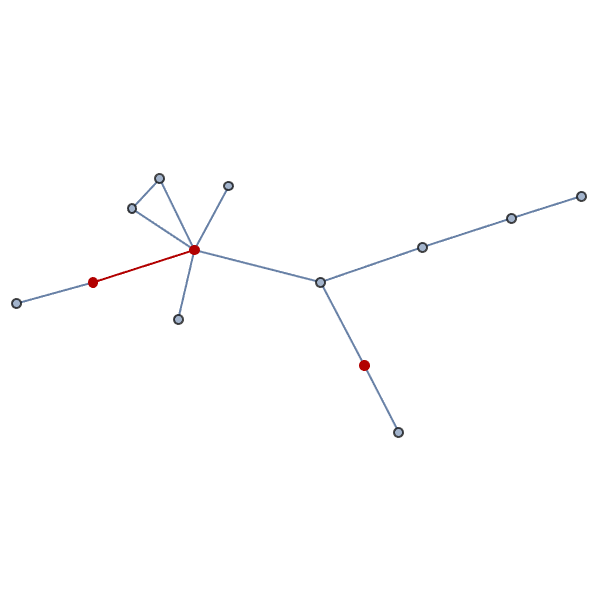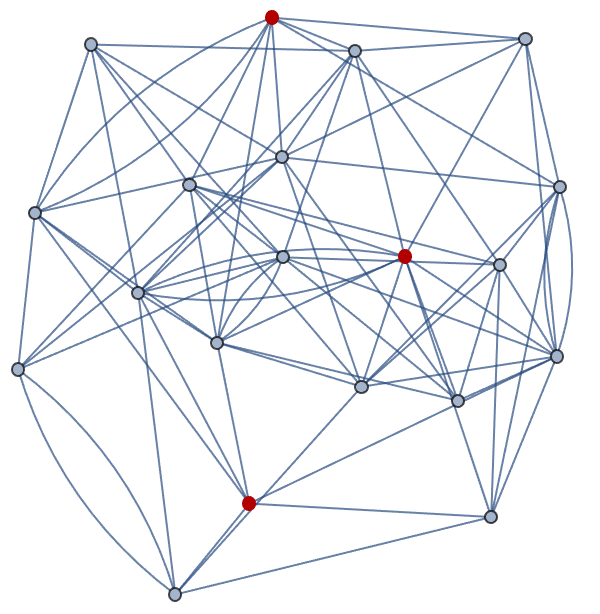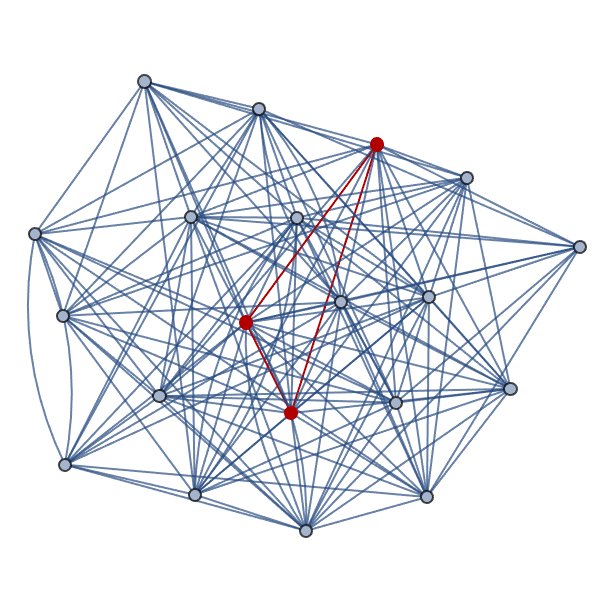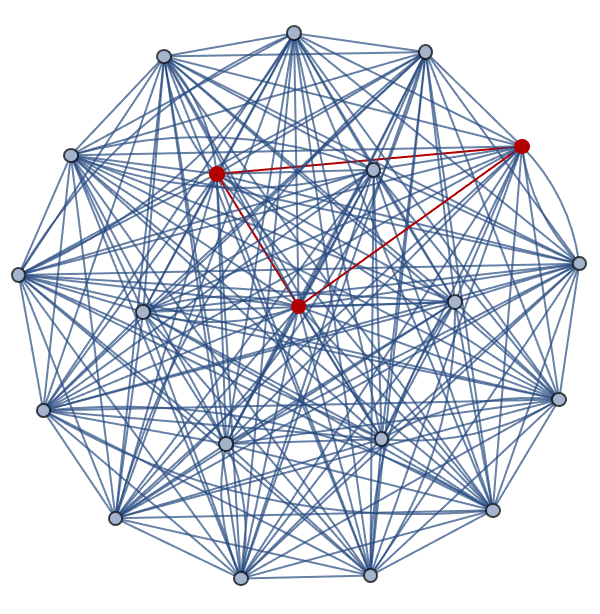
That is the @Peter Burbery master-class in Package Management.
ListAnimate[Table[
RandomGraph[{50, 120},
VertexShapeFunction -> "Circle",
VertexStyle -> Hue[RandomReal[]],
EdgeStyle -> Directive[Opacity[0.7], Hue[RandomReal[]]]
], {i, 50}]]
Whenever you're able to get all these resources just remember to feel free to post them.
g = RandomWeightedMixedGraph[SpatialGraphDistribution[100, 0.06], 0.8,
RandomInteger[{1, 5}] &]

When I saw all the versions in that directory, I said to myself this brings forward so many loops and the minimum cost traversals of these mixed graphs, covering each edge at least once.
petersen = PetersenGraph[];
GraphConvexHull[petersen, {1, 2, 3, 4, 5}]
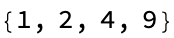
So when you see the PacletSymbol, it makes it possible to generate and manipulate mixed graphs.
g = RandomGraph[BarabasiAlbertGraphDistribution[100, 2],
VertexStyle -> Directive[EdgeForm[None], FaceForm[White]],
VertexSize -> 0.5, ImageSize -> Large]

The paclet can also construct random mixed graphs, the specific features like the weighted edges and directed arcs and yes, the convex hull.
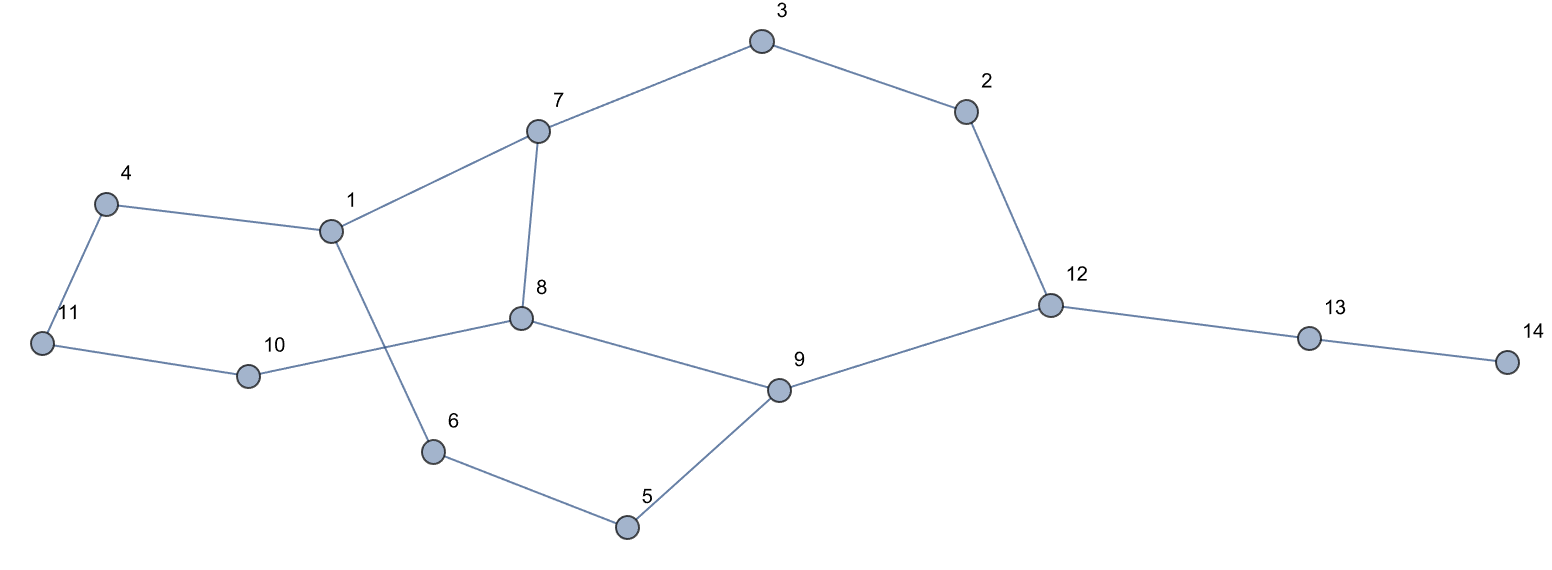
convexHull =
Graph[{1 \[UndirectedEdge] 4, 4 \[UndirectedEdge] 11,
11 \[UndirectedEdge] 10, 10 \[UndirectedEdge] 8,
8 \[UndirectedEdge] 7, 7 \[UndirectedEdge] 1,
8 \[UndirectedEdge] 9, 7 \[UndirectedEdge] 3,
2 \[UndirectedEdge] 3, 2 \[UndirectedEdge] 12,
12 \[UndirectedEdge] 13, 13 \[UndirectedEdge] 14,
12 \[UndirectedEdge] 9, 9 \[UndirectedEdge] 5,
5 \[UndirectedEdge] 6, 6 \[UndirectedEdge] 1},
VertexLabels -> Automatic]
GraphConvexHull[convexHull, {1, 2, 9}]
Users can select the undirected edge set and the directed arc set of a mixed graph, with MixedGraphUndirectedEdges and MixedGraphDirectedArcs.
SeedRandom[435];
pg = PetersenGraph[];
n = VertexCount[pg];
g = RandomWeightedMixedGraph[
SpatialGraphDistribution[n, 0.2],
EdgeCount[pg]/Binomial[n, 2],
RandomInteger[{1, 7}] &
]

I can also specify options, the function GraphConvexHull can compute the convex hull of a graph via those options, based on the initial conditions that specify the nodes.
SeedRandom[28905];
g = RandomGraph[
{50, 100},
EdgeStyle -> Directive[Opacity[0.5], Hue[RandomReal[]]],
VertexSize -> Large,
VertexLabels -> Automatic,
GraphLayout -> "SpringEmbedding"
]
By the way @Peter Burbery if we can compute via GraphInformation, we can find Boolean properties of graphs and can...via TakeLargestGraphComponentBy an objective function we can find graph components.
RandomWeightedMixedGraph[
BarabasiAlbertGraphDistribution[30, 2],
0.8,
RandomInteger[{1, 10}],
VertexSize -> 0.7,
VertexStyle -> LightBlue,
VertexShapeFunction -> "Diamond",
EdgeStyle -> Directive[Thickness[0.007], Opacity[0.7]],
VertexLabels -> Placed["Name", Center],
ImageSize -> Large]
Even though the function EulerianGraphQ does not support mixed graphs, that topic of research is my way to go @Peter Burbery when I saw how many notebooks you had it was like night and day.
RandomWeightedMixedGraph[
{50, 150},
0.2,
RandomReal[{0, 1}] &,
VertexShapeFunction -> "Star",
VertexSize -> Medium,
EdgeStyle -> Directive[GrayLevel[0.6], Thin],
VertexStyle ->
Directive[GrayLevel[0.4], EdgeForm[Black], Opacity[0.8]]]
The Paclet repository, thought I had some boolean properties of graphs and said that must be Peter!
RandomWeightedMixedGraph[BarabasiAlbertGraphDistribution[54, 3], 0.68,
RandomInteger[{1, 7}] &, GraphLayout -> "SpectralEmbedding",
ImageSize -> 500]
With distributions like this for the underlying graph, it's so great to be able to generate these Edge Themes and yes, Plot Weights.
RandomMixedGraph[BarabasiAlbertGraphDistribution[200, 4], 0.8,
PlotTheme -> "LargeGraph"]

What's the probability of directed edges?
RandomMixedGraph[BarabasiAlbertGraphDistribution[54, 3], 0.68,
PlotTheme -> "LargeGraph"]

And it loops around and it loops but only if the edge was originally an undirected edge.
RandomMixedGraph[
BarabasiAlbertGraphDistribution[100, 5],
0.7,
VertexStyle -> White,
VertexSize -> Large,
EdgeStyle -> Directive[Thick, Dashed, Red],
Background -> Black,
ImageSize -> Large,
GraphLayout -> "SpectralEmbedding"
]
How do you select the largest component based on an objective function?
RandomMixedGraph[
BarabasiAlbertGraphDistribution[100, 5],
0.7,
VertexStyle -> White,
VertexSize -> Large,
EdgeStyle -> Directive[Thick, Dashed, Red],
Background -> Black,
ImageSize -> Large,
GraphLayout -> "CircularEmbedding"
]
When I saw the quantity of valuable stuff that you have produced, it wasn't just the Paclet, the PacletInstall, the $path and when I saw the Block Context it was like none other.
RandomMixedGraph[
BarabasiAlbertGraphDistribution[100, 5],
0.7,
VertexStyle -> White,
VertexSize -> Large,
EdgeStyle -> Directive[Thick, Dashed, Red],
Background -> Black,
ImageSize -> Large,
GraphLayout -> "SpiralEmbedding"
]

@Peter Burbery your documentation, the submission of this paclet is on fleek, your implementation of the MCPP is like my dream come true.
RandomMixedGraph[{20, 54}, 0.68, {2, 3, 5}, ImageSize -> 50]
RandomMixedGraph[BarabasiAlbertGraphDistribution[54, 3], 0.68]
RandomMixedGraph[BarabasiAlbertGraphDistribution[1000, 3], 0.68,
PlotTheme -> "LargeGraph"]
RandomMixedGraph[BarabasiAlbertGraphDistribution[54, 3], 0.68, 7]
RandomMixedGraph[BarabasiAlbertGraphDistribution[100, 3], 0.68,
GraphLayout -> "LayeredDigraphEmbedding",
EdgeStyle -> Directive[Thickness[0.001], Hue[RandomReal[]]],
VertexStyle -> Directive[EdgeForm[], Hue[RandomReal[]]],
ImageSize -> 600
]
RandomMixedGraph[{20, 54},
0.68,
{2, 3, 5},
ImageSize -> 400,
GraphStyle -> "VintageDiagram",
VertexStyle -> Directive[EdgeForm[], Hue[RandomReal[]]],
EdgeStyle -> Directive[Thickness[0.02], Hue[RandomReal[]]]
]

Do not hesitate to post!


Is this the difference between Version 1.22.0 and 1.21.0? Peter this is sweet.

The random mixed graphs with random weights, they're made of diamonds. Please excuse me I am just so blessed to have met you because this NP-hard problem is my path to a bright future. I will always remember you, Peter.
RandomMixedGraph[BarabasiAlbertGraphDistribution[54, 3], 0.68,
PlotTheme -> "LargeGraph"]
RandomMixedGraph[{40, 80}, 0.8, 7, ImageSize -> Medium,
PlotTheme -> "Scientific"]
RandomMixedGraph[BarabasiAlbertGraphDistribution[100, 3], 0.6,
VertexShapeFunction -> "Star", VertexSize -> Medium,
VertexStyle -> LightBlue, EdgeStyle -> Directive[Thick, Orange],
ImageSize -> Large, PlotTheme -> "Web"]
\[ScriptCapitalG] = RandomMixedGraph[{20, 54}, 0.68];
FindGraphCommunities[\[ScriptCapitalG], Method -> "Modularity"]
HighlightGraph[\[ScriptCapitalG],
Subgraph[\[ScriptCapitalG], #] & /@
FindGraphCommunities[\[ScriptCapitalG], Method -> "Modularity"],
ImageSize -> Medium]
\[ScriptCapitalG] =
RandomMixedGraph[BarabasiAlbertGraphDistribution[54, 3], 0.68];
FindGraphCommunities[\[ScriptCapitalG], Method -> "Modularity"]
HighlightGraph[\[ScriptCapitalG],
Subgraph[\[ScriptCapitalG], #] & /@
FindGraphCommunities[\[ScriptCapitalG], Method -> "Modularity"],
ImageSize -> Medium]
RandomMixedGraph[BarabasiAlbertGraphDistribution[50, 3], 0.7]
RandomMixedGraph[BarabasiAlbertGraphDistribution[50, 2], 0.5]



Peter this is brilliant we couldn't even begin to imagine what it's like the damage that has been done to the Paclet Repository, it's all these functions that are built into your mixed graphs, your digraphs, and your weighted edges and directed arcs.