Message Boards Message Boards

[WSS22] Mixed Chinese postman problem MCPP implementation

POSTED BY: Peter Burbery
3 Replies
Sort By:

enter image description here -- you have earned Featured Contributor Badge enter image description here Your exceptional post has been selected for our editorial column Staff Picks http://wolfr.am/StaffPicks and Your Profile is now distinguished by a Featured Contributor Badge and is displayed on the Featured Contributor Board. Thank you!
POSTED BY: EDITORIAL BOARD

@Peter Burbery it's the hand-waving, the development of the Mixed Chinese Postman Problem, that gets us the optimum tour for a mixed graph. 

PacletInstall["PeterBurbery/MixedGraphs"];
%["Location"];
PacletDirectoryLoad[
  "/Users/deangladish/mixed-graphs-paclet/Mixed Graphs"];
PacletInstall[
  "/Users/deangladish/mixed-graphs-paclet/Mixed \
Graphs/build/PeterBurbery__MixedGraphs-1.21.0.paclet"];
PacletFind["PeterBurbery/MixedGraphs"]
Information[PacletObject["PeterBurbery/MixedGraphs"]]
$ContextPath;
Directory[];

Paclet Install

PacletObject

Paclet Information

And then your GitHub, the MixedGraphs that allows us to get so many versions on ~/mixed-graphs-paclet/ and in Mixed Graphs/build, and there are so many .nbs in the directory, Peter, we can get them directly. 

Get["/Users/deangladish/mixed-graphs-paclet/Mixed \
Graphs/build/PeterBurbery__MixedGraphs/Kernel/MixedGraphs.wl"]

Differentiating between Version 1.22.0 and 1.21.0. 

Animate[Module[{g}, 
  g = RandomGraph[BernoulliGraphDistribution[20, p], ImageSize -> 300];
  g = First[TakeLargestGraphComponentBy[g]];
  g = EulerizeGraph[g];
  HighlightGraph[g, Subgraph[g, RandomSample[VertexList[g], 3]]]], {p,
   0.1, 1, 0.1}]

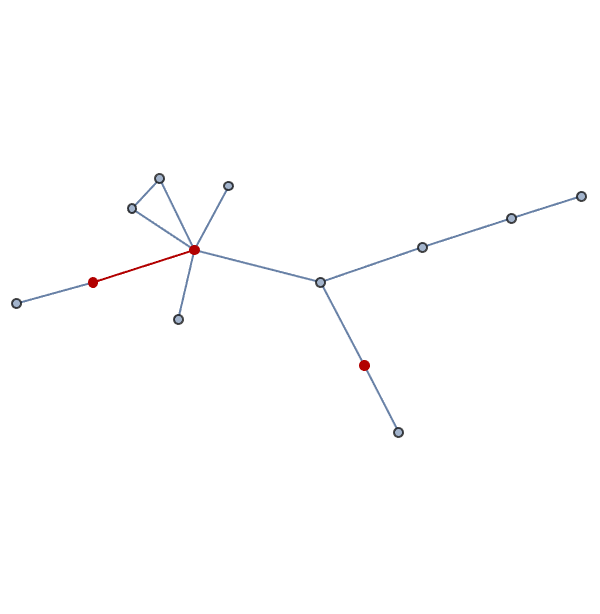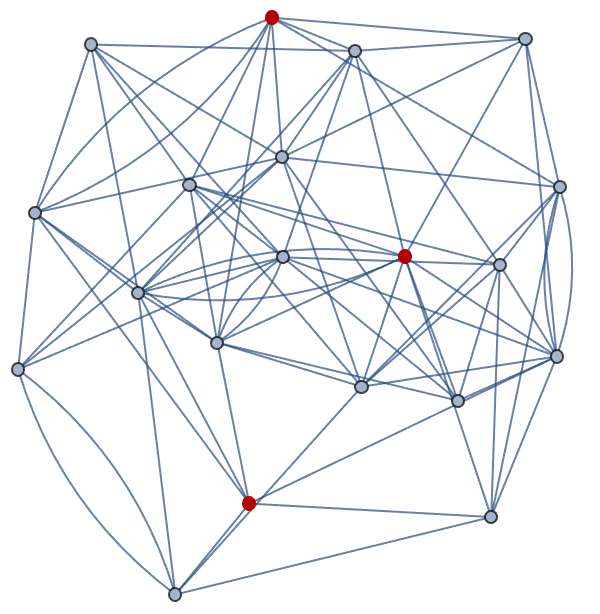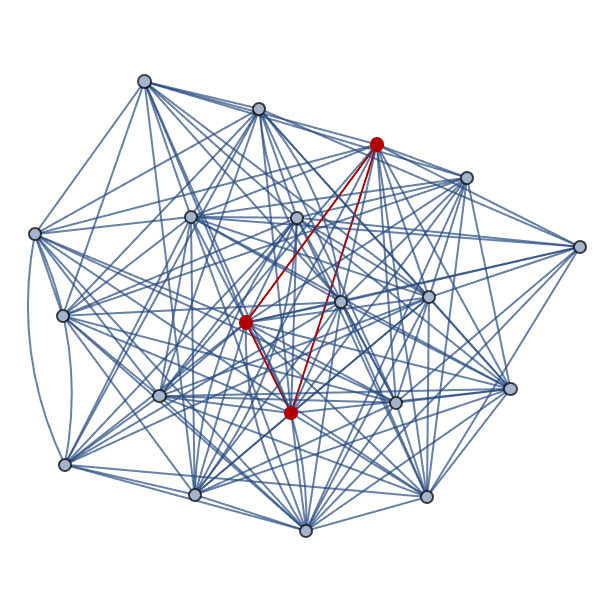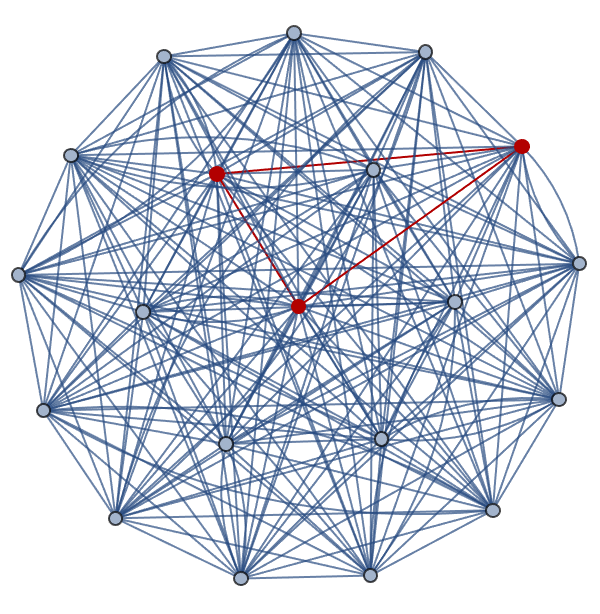
BernoulliGraphDistribution

That is the @Peter Burbery master-class in Package Management. 

ListAnimate[Table[
  RandomGraph[{50, 120},
   VertexShapeFunction -> "Circle",
   VertexStyle -> Hue[RandomReal[]],
   EdgeStyle -> Directive[Opacity[0.7], Hue[RandomReal[]]]
   ], {i, 50}]]

ListAnimate RandomGraph

Whenever you're able to get all these resources just remember to feel free to post them. 

g = RandomWeightedMixedGraph[SpatialGraphDistribution[100, 0.06], 0.8,
   RandomInteger[{1, 5}] &]

RandomWeightedMixedGraph

When I saw all the versions in that directory, I said to myself this brings forward so many loops and the minimum cost traversals of these mixed graphs, covering each edge at least once. 

petersen = PetersenGraph[];
GraphConvexHull[petersen, {1, 2, 3, 4, 5}]

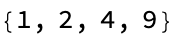
Petersen Convex Hull

So when you see the PacletSymbol, it makes it possible to generate and manipulate mixed graphs. 

g = RandomGraph[BarabasiAlbertGraphDistribution[100, 2], 
  VertexStyle -> Directive[EdgeForm[None], FaceForm[White]], 
  VertexSize -> 0.5, ImageSize -> Large]

BarabasiAlbertGraphDistribution

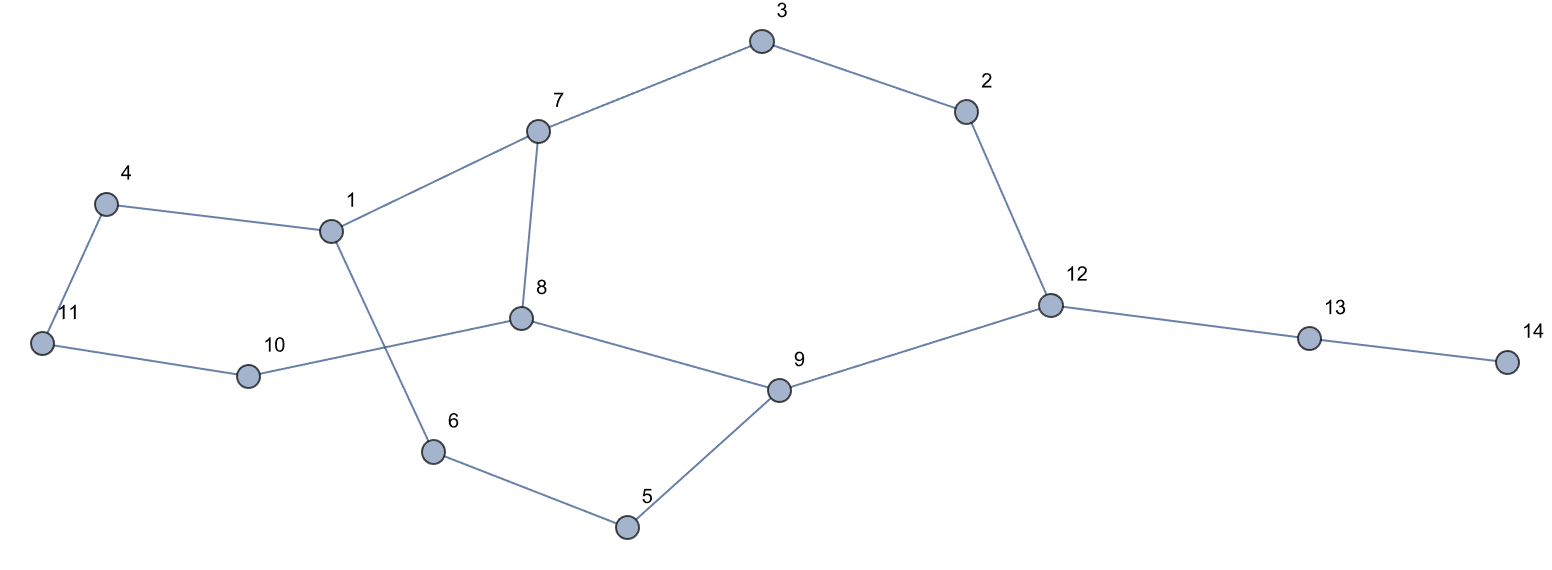
The paclet can also construct random mixed graphs, the specific features like the weighted edges and directed arcs and yes, the convex hull.

convexHull = 
 Graph[{1 \[UndirectedEdge] 4, 4 \[UndirectedEdge] 11, 
   11 \[UndirectedEdge] 10, 10 \[UndirectedEdge] 8, 
   8 \[UndirectedEdge] 7, 7 \[UndirectedEdge] 1, 
   8 \[UndirectedEdge] 9, 7 \[UndirectedEdge] 3, 
   2 \[UndirectedEdge] 3, 2 \[UndirectedEdge] 12, 
   12 \[UndirectedEdge] 13, 13 \[UndirectedEdge] 14, 
   12 \[UndirectedEdge] 9, 9 \[UndirectedEdge] 5, 
   5 \[UndirectedEdge] 6, 6 \[UndirectedEdge] 1}, 
  VertexLabels -> Automatic]
GraphConvexHull[convexHull, {1, 2, 9}]

Convex Hull

Graph Convex Hull

Users can select the undirected edge set and the directed arc set of a mixed graph, with MixedGraphUndirectedEdges and MixedGraphDirectedArcs. 

SeedRandom[435];
pg = PetersenGraph[];
n = VertexCount[pg];
g = RandomWeightedMixedGraph[
  SpatialGraphDistribution[n, 0.2],
  EdgeCount[pg]/Binomial[n, 2],
  RandomInteger[{1, 7}] &
  ]

Seed 435

I can also specify options, the function GraphConvexHull can compute the convex hull of a graph via those options, based on the initial conditions that specify the nodes. 

SeedRandom[28905];
g = RandomGraph[
  {50, 100},
  EdgeStyle -> Directive[Opacity[0.5], Hue[RandomReal[]]],
  VertexSize -> Large,
  VertexLabels -> Automatic,
  GraphLayout -> "SpringEmbedding"
  ]

Seed 28905

By the way @Peter Burbery if we can compute via GraphInformation, we can find Boolean properties of graphs and can...via TakeLargestGraphComponentBy an objective function we can find graph components. 

RandomWeightedMixedGraph[
 BarabasiAlbertGraphDistribution[30, 2],
 0.8,
 RandomInteger[{1, 10}],
 VertexSize -> 0.7,
 VertexStyle -> LightBlue,
 VertexShapeFunction -> "Diamond",
 EdgeStyle -> Directive[Thickness[0.007], Opacity[0.7]],
 VertexLabels -> Placed["Name", Center],
 ImageSize -> Large]

Random Weighted Mixed Graph Barabasi

Even though the function EulerianGraphQ does not support mixed graphs, that topic of research is my way to go @Peter Burbery when I saw how many notebooks you had it was like night and day. 

RandomWeightedMixedGraph[
 {50, 150},
 0.2,
 RandomReal[{0, 1}] &,
 VertexShapeFunction -> "Star",
 VertexSize -> Medium,
 EdgeStyle -> Directive[GrayLevel[0.6], Thin], 
 VertexStyle -> 
  Directive[GrayLevel[0.4], EdgeForm[Black], Opacity[0.8]]]

Star Graph

The Paclet repository, thought I had some boolean properties of graphs and said that must be Peter!

RandomWeightedMixedGraph[BarabasiAlbertGraphDistribution[54, 3], 0.68,
  RandomInteger[{1, 7}] &, GraphLayout -> "SpectralEmbedding", 
 ImageSize -> 500]

SpectralEmbedding

With distributions like this for the underlying graph, it's so great to be able to generate these Edge Themes and yes, Plot Weights. 

RandomMixedGraph[BarabasiAlbertGraphDistribution[200, 4], 0.8, 
 PlotTheme -> "LargeGraph"]

Large Graph

What's the probability of directed edges? 

RandomMixedGraph[BarabasiAlbertGraphDistribution[54, 3], 0.68, 
 PlotTheme -> "LargeGraph"]

Smaller Graph

And it loops around and it loops but only if the edge was originally an undirected edge. 

RandomMixedGraph[
 BarabasiAlbertGraphDistribution[100, 5],
 0.7,
 VertexStyle -> White,
 VertexSize -> Large,
 EdgeStyle -> Directive[Thick, Dashed, Red],
 Background -> Black,
 ImageSize -> Large,
 GraphLayout -> "SpectralEmbedding"
 ]

Spectral Black

How do you select the largest component based on an objective function? 

RandomMixedGraph[
 BarabasiAlbertGraphDistribution[100, 5],
 0.7,
 VertexStyle -> White,
 VertexSize -> Large,
 EdgeStyle -> Directive[Thick, Dashed, Red],
 Background -> Black,
 ImageSize -> Large,
 GraphLayout -> "CircularEmbedding"
 ]

Circular Embedding

When I saw the quantity of valuable stuff that you have produced, it wasn't just the Paclet, the PacletInstall, the $path and when I saw the Block Context it was like none other. 

RandomMixedGraph[
 BarabasiAlbertGraphDistribution[100, 5],
 0.7,
 VertexStyle -> White,
 VertexSize -> Large,
 EdgeStyle -> Directive[Thick, Dashed, Red],
 Background -> Black,
 ImageSize -> Large,
 GraphLayout -> "SpiralEmbedding"
 ]

Spiral Embedding

@Peter Burbery your documentation, the submission of this paclet is on fleek, your implementation of the MCPP is like my dream come true. 

RandomMixedGraph[{20, 54}, 0.68, {2, 3, 5}, ImageSize -> 50]
RandomMixedGraph[BarabasiAlbertGraphDistribution[54, 3], 0.68]
RandomMixedGraph[BarabasiAlbertGraphDistribution[1000, 3], 0.68, 
 PlotTheme -> "LargeGraph"]
RandomMixedGraph[BarabasiAlbertGraphDistribution[54, 3], 0.68, 7]
RandomMixedGraph[BarabasiAlbertGraphDistribution[100, 3], 0.68,
 GraphLayout -> "LayeredDigraphEmbedding",
 EdgeStyle -> Directive[Thickness[0.001], Hue[RandomReal[]]],
 VertexStyle -> Directive[EdgeForm[], Hue[RandomReal[]]],
 ImageSize -> 600
 ]
RandomMixedGraph[{20, 54},
 0.68,
 {2, 3, 5},
 ImageSize -> 400,
 GraphStyle -> "VintageDiagram",
 VertexStyle -> Directive[EdgeForm[], Hue[RandomReal[]]],
 EdgeStyle -> Directive[Thickness[0.02], Hue[RandomReal[]]]
 ]

dist1

Do not hesitate to post!

dist2

dist3

dist4

Is this the difference between Version 1.22.0 and 1.21.0? Peter this is sweet.

distdigraph

distvintage

The random mixed graphs with random weights, they're made of diamonds. Please excuse me I am just so blessed to have met you because this NP-hard problem is my path to a bright future. I will always remember you, Peter. 

RandomMixedGraph[BarabasiAlbertGraphDistribution[54, 3], 0.68, 
 PlotTheme -> "LargeGraph"]
RandomMixedGraph[{40, 80}, 0.8, 7, ImageSize -> Medium, 
 PlotTheme -> "Scientific"]
RandomMixedGraph[BarabasiAlbertGraphDistribution[100, 3], 0.6, 
 VertexShapeFunction -> "Star", VertexSize -> Medium, 
 VertexStyle -> LightBlue, EdgeStyle -> Directive[Thick, Orange], 
 ImageSize -> Large, PlotTheme -> "Web"]
\[ScriptCapitalG] = RandomMixedGraph[{20, 54}, 0.68];
FindGraphCommunities[\[ScriptCapitalG], Method -> "Modularity"]
HighlightGraph[\[ScriptCapitalG], 
 Subgraph[\[ScriptCapitalG], #] & /@ 
  FindGraphCommunities[\[ScriptCapitalG], Method -> "Modularity"], 
 ImageSize -> Medium]
\[ScriptCapitalG] = 
  RandomMixedGraph[BarabasiAlbertGraphDistribution[54, 3], 0.68];
FindGraphCommunities[\[ScriptCapitalG], Method -> "Modularity"]
HighlightGraph[\[ScriptCapitalG], 
 Subgraph[\[ScriptCapitalG], #] & /@ 
  FindGraphCommunities[\[ScriptCapitalG], Method -> "Modularity"], 
 ImageSize -> Medium]
RandomMixedGraph[BarabasiAlbertGraphDistribution[50, 3], 0.7]
RandomMixedGraph[BarabasiAlbertGraphDistribution[50, 2], 0.5]

rand1

rand2

rand3

rand4

rand5

rand6

rand7

rand8

rand9

Peter this is brilliant we couldn't even begin to imagine what it's like the damage that has been done to the Paclet Repository, it's all these functions that are built into your mixed graphs, your digraphs, and your weighted edges and directed arcs.

POSTED BY: Dean Gladish

There is a paid service integrated with another paid service that might have support for the windy Chinese postman problem, which contains the MCPP as a special case. Suppose you have access to ArcGIS Pro by ESRI. In that case, there is RouteSmart which offers Routing as a service RaaS and consulting to people who want to find the most efficient routes, for example, for snow plowing and newspaper delivery and other types of delivery like mail delivery and package delivery. I have access to ArcGIS Pro because I'm taking a GIS class, but I don't have access to RouteSmart's RaaS. I think they mainly hire people with PhDs to work on specialized algorithms.
POSTED BY: Peter Burbery
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract