Cellular automata have some greater implications beyond mathematical curiosity--when you see what they're offering, the computational universality as well as complexity theory of cellular automata becomes more apparent. And I knew, the visualization and understanding of complex 3D cellular automata opens pathways into the simulation of physical phenomena with regard to time travel and additive manufacturing processes like 3D printing. In this demonstration, we visualize a cellular automaton evolving over discrete time steps. A basic 3D Cellular Automaton Visualization, the rule {10, {2, 1}, {1, 1, 1}} governs cell evolution, demonstrating how simple rules lead to complex, unpredictable structures. Such visualizations form the basis for exploring automata properties.
Manipulate[
Module[{myGrid, myCubes},
myGrid =
CellularAutomaton[{6, {2, 1}, {1, 1, 1}}, {{{{1}}}, 0}, {{{t}}}];
myCubes =
Map[With[{pos = #}, {Directive[Opacity[0.8],
Specularity[White, 30], ColorData["Rainbow"][pos[[3]]/20]],
Cuboid[pos]}] &, Position[myGrid, 1]];
Graphics3D[{EdgeForm[], myCubes},
ViewPoint -> {15 Cos[0.1 t], 15 Sin[0.1 t], 10},
ImageSize -> Large, PlotRange -> {{0, 20}, {0, 20}, {0, 20}},
SphericalRegion -> True, Lighting -> "Neutral",
Background -> Transparent, Boxed -> False]], {t, 0, 50, 1,
Appearance -> "Labeled"}, SaveDefinitions -> True]


Using Manipulate alongside Graphics3D, this interactive environment allows users to rotate and translate the view and thus makes it possible to reveal internal structures that are otherwise obscured, aiding our comprehension of spatial relationships within the automaton. Intuitively, these complex three-dimensional structures make it possible for users to rotate around the automaton and color cubes based on their vertical positions. Users can explore how minor variations in parameters dramatically impact the resulting automaton, offering a beautiful perspective into the realm of complexity as it hatches.
Manipulate[
Module[{ca},
ca = CellularAutomaton[{rule, {2, 1}, {1, 1, 1}}, {{{{1}}},
0}, {{{steps}}}];
ArrayPlot3D[ca,
ViewPoint -> {distance*Sin[\[Theta]], distance*Cos[\[Theta]],
height}, ImageSize -> 600,
ColorFunction -> (ToExpression[color] &),
ColorFunctionScaling -> False, Boxed -> False, Axes -> False,
Lighting -> "Neutral", PlotRangePadding -> None,
SphericalRegion -> True]], {{steps, 3, "Evolution Steps"}, 0, 10,
1, Appearance -> "Labeled"}, {{rule, 10, "Rule"}, {2, 6, 10},
ControlType -> PopupMenu}, {{distance, 5, "Camera Distance"}, 3, 10,
0.1, Appearance -> "Labeled"}, {{height, 2, "Camera Height"}, 1, 5,
0.1, Appearance -> "Labeled"}, {{\[Theta], 0, "View Angle"}, 0,
2 Pi, AnimationRate -> 0.5,
Appearance -> "Labeled"}, {{color, "Red", "Color"}, {"Red", "Green",
"Blue", "Black", "White"}}, ControlPlacement -> Left,
TrackedSymbols :> {steps, rule, distance, height, \[Theta], color},
SaveDefinitions -> True]

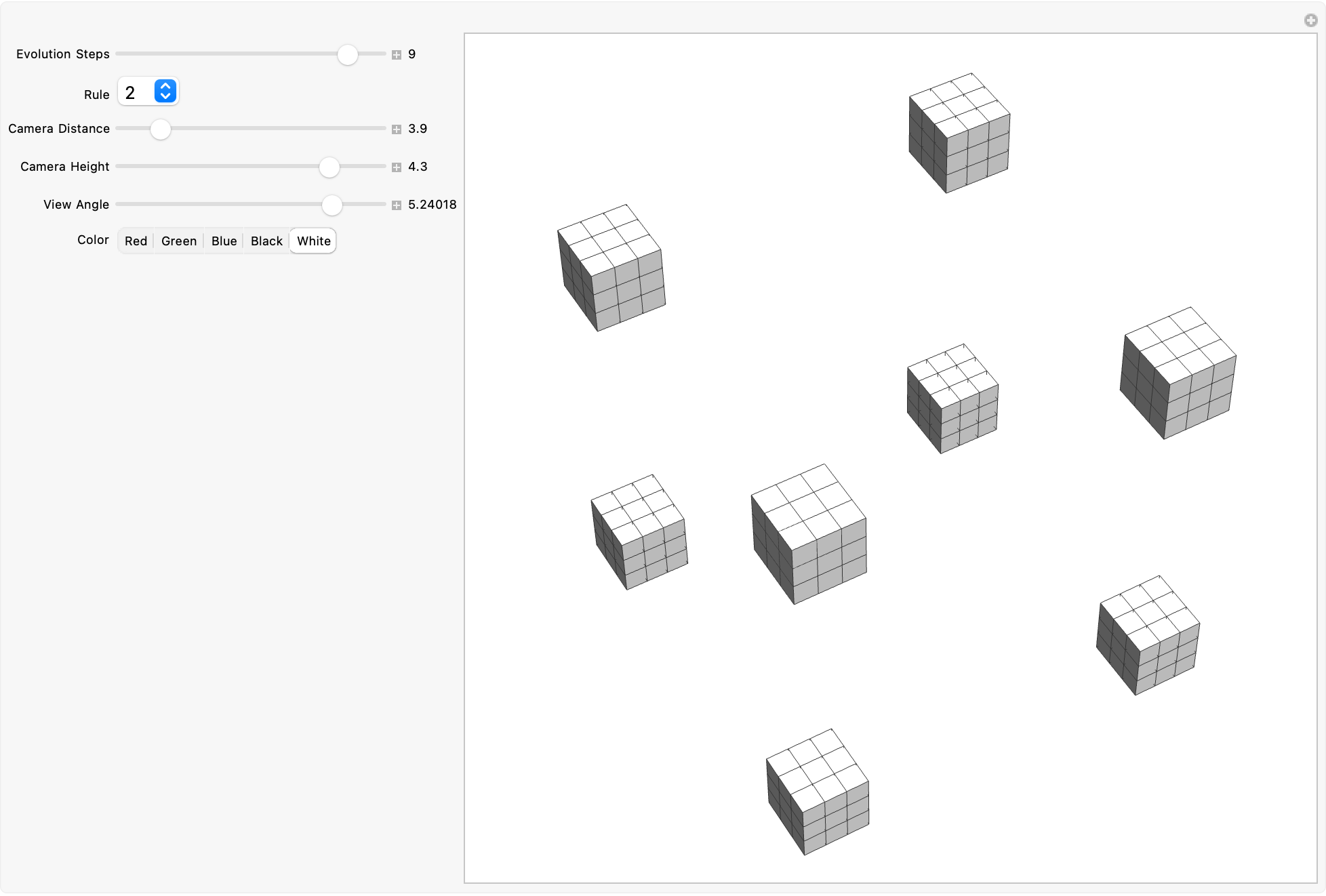
Its fine-grained settings encourage users to explore the iterative exploration process, promoting a meaningful understanding of cellular automata's circuitous as well as dynamic complexity, which serves as a valuable educational and research tool to model how tiny initial differences in the automaton's setup or rule sets can cause drastically different evolutionary outcomes within the mesh of theoretical fascination, holding significant implications for modeling biological systems. The visualization methods outlined here can assist researchers in modeling and analyzing these complex phenomena such as ecological patterns, crowd-related chaos theory, and systemic urban growth. Potential future research can explore integrating cellular automata with machine learning to predict complex behavior patterns. Virtual reality versioning could also facilitate immersive experiences, significantly building the experiential learning aspect of researchers and educators alike.
Manipulate[
Module[{grid, \[Theta], cubes, cameraPos, center},
grid = CellularAutomaton[{10, {2, 1}, {1, 1, 1}}, {{{{1}}},
0}, {{{Round[t]}}}];
center = {5, 5, 5};
\[Theta] = t*rotationSpeed;
cubes = Position[grid, 1];
cameraPos =
center + {cameraDistance Cos[\[Theta]],
cameraDistance Sin[\[Theta]], cameraHeight};
Graphics3D[{EdgeForm[None], {Blend[{color1, color2}, Sin[t/5]^2],
Specularity[White, 10 + 90 specularity], Cuboid /@ cubes},
If[showAxes, {Gray, Thick, Line[{{0, 0, 0}, {10, 0, 0}}],
Line[{{0, 0, 0}, {0, 10, 0}}],
Line[{{0, 0, 0}, {0, 0, 10}}]}, {}]}, Boxed -> False,
ViewPoint -> cameraPos, ViewVertical -> {0, 0, 1},
PlotRange -> {{0, 10}, {0, 10}, {0, 10}}, ImageSize -> 600,
Lighting -> {{"Ambient", GrayLevel[0.1]}, {"Directional",
directionalLight, {5, 5, 20}}}, Background -> bgColor,
SphericalRegion -> True,
Method -> {"LightingModel" -> "Phong"}]], {{t, 1, "Time"}, 1, 30,
1, Appearance -> "Labeled", AnimationRate -> 2},
Row[{Column[{Control[{{rotationSpeed, 0.2, "Rotation Speed"}, 0, 1}],
Control[{{cameraDistance, 20, "Camera Distance"}, 10, 40}],
Control[{{cameraHeight, 15, "Camera Height"}, 5, 30}],
Control[{{specularity, 0.8, "Surface Shine"}, 0, 1}]}],
Column[{Control[{{color1, Blue, "Primary Color"}, ColorSlider}],
Control[{{color2, Cyan, "Secondary Color"}, ColorSlider}],
Control[{{ambientLight, GrayLevel[0.1], "Ambient Light"},
ColorSlider}],
Control[{{directionalLight, White, "Directional Light"},
ColorSlider}]}],
Column[{Control[{{bgColor, Black, "Background"}, ColorSlider}],
Control[{{showAxes, False, "Show Axes"}, {True, False}}],
Button["Reset", t = 1; rotationSpeed = 0.2;
cameraDistance = 20; cameraHeight = 15; specularity = 0.8;
color1 = Blue; color2 = Cyan;
ambientLight = GrayLevel[0.1]; directionalLight = White;
bgColor = Black]}]}], SaveDefinitions -> True,
TrackedSymbols :> {t, rotationSpeed, cameraDistance, cameraHeight,
specularity, color1, color2, ambientLight, directionalLight,
bgColor, showAxes}, SynchronousUpdating -> False]
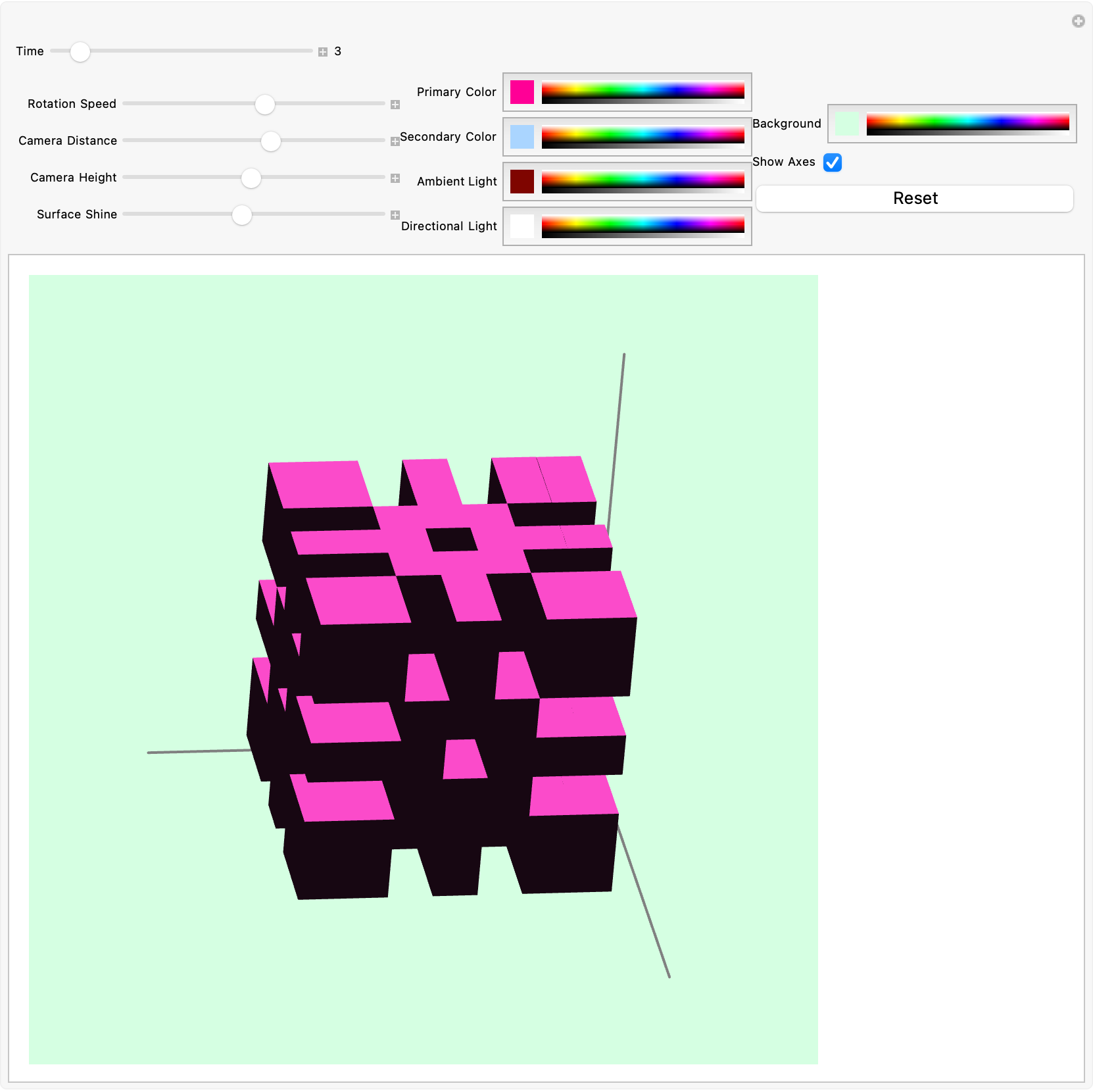

Altering parameters such as x, y, z, a, b, c and angle t coordinate inter-spatial relationships within the automaton, maximizing exposure to unseen cells, combining generateViewVectors and generateViewPoints heuristically to determine optimal viewing paths. Our critical interests are in updating the computational aesthetics and observing global automaton structure; one panel offers a fixed infinite viewpoint ideal for observing surface reflectivity and realism, while the other allows variable positioning to examine the local cellular metaphor of augmented reality as a fixed infinite point of view. Thank you so much, for this project and doing all the things we need to make it doable, it's pretty cool @Madelyn Mao seeing the unseen this is unreal, because a cellular automaton is really just a series of cells that exist, according to a specific rule.
Row[{
Manipulate[
Dynamic@Graphics3D[
{
Cuboid[#, # + 1] & /@ Position[
ArrayPad[
CellularAutomaton[
{224, {2, {{2, 2, 2}, {2, 1, 2}, {2, 2, 2}}}, {1, 1}},
RandomInteger[1, {50, 50}],
{{0, 1}}], 1]
, 1]
},
ViewPoint -> {Infinity, Infinity, Infinity},
Boxed -> False,
ViewAngle -> t],
{{t, 1.8, "View Angle"}, 1.8, 2, .01},
SaveDefinitions -> True
],
Manipulate[
Graphics3D[
{
RGBColor[
RandomReal[{0, 1}, 3, WorkingPrecision -> MachinePrecision]^0.1],
Opacity[0.75],
Specularity[White, 50],
EdgeForm[{Thickness[0.001], Blue}],
Cuboid[#, # + 1] & /@ Position[
ArrayPad[
CellularAutomaton[
{540 + 882, {2, 1}, {1, 1, 1}},
{{{{1}}}, 0},
{{{3}}}
], 1], 1]
},
Boxed -> False,
ViewPoint -> {15 + x, 15 + y, 15 + z},
ViewVector -> {{a, b, c}, {15, 15, 15}},
ViewAngle -> t],
{{t, 1.3, "View Angle"}, 1.3, 2.5, .01},
{{x, 0, "X displacement"}, -3, 3, 1},
{{y, 0, "Y displacement"}, -3, 3, 1},
{{z, 0, "Z displacement"}, -3, 3, 1},
{{a, 0, "View vector X"}, -1, 1, .1},
{{b, 0, "View vector Y"}, -1, 1, .1},
{{c, 0, "View vector Z"}, -1, 1, .1},
SaveDefinitions -> True
]
}]
These cellular automatons are mostly cube shaped, it's not like those hexagons and Sierpinski triangles or anything like the fractals, the Game of Life...Conway? Simple rules are creating complicated shapes without intervention, from the initial settings.
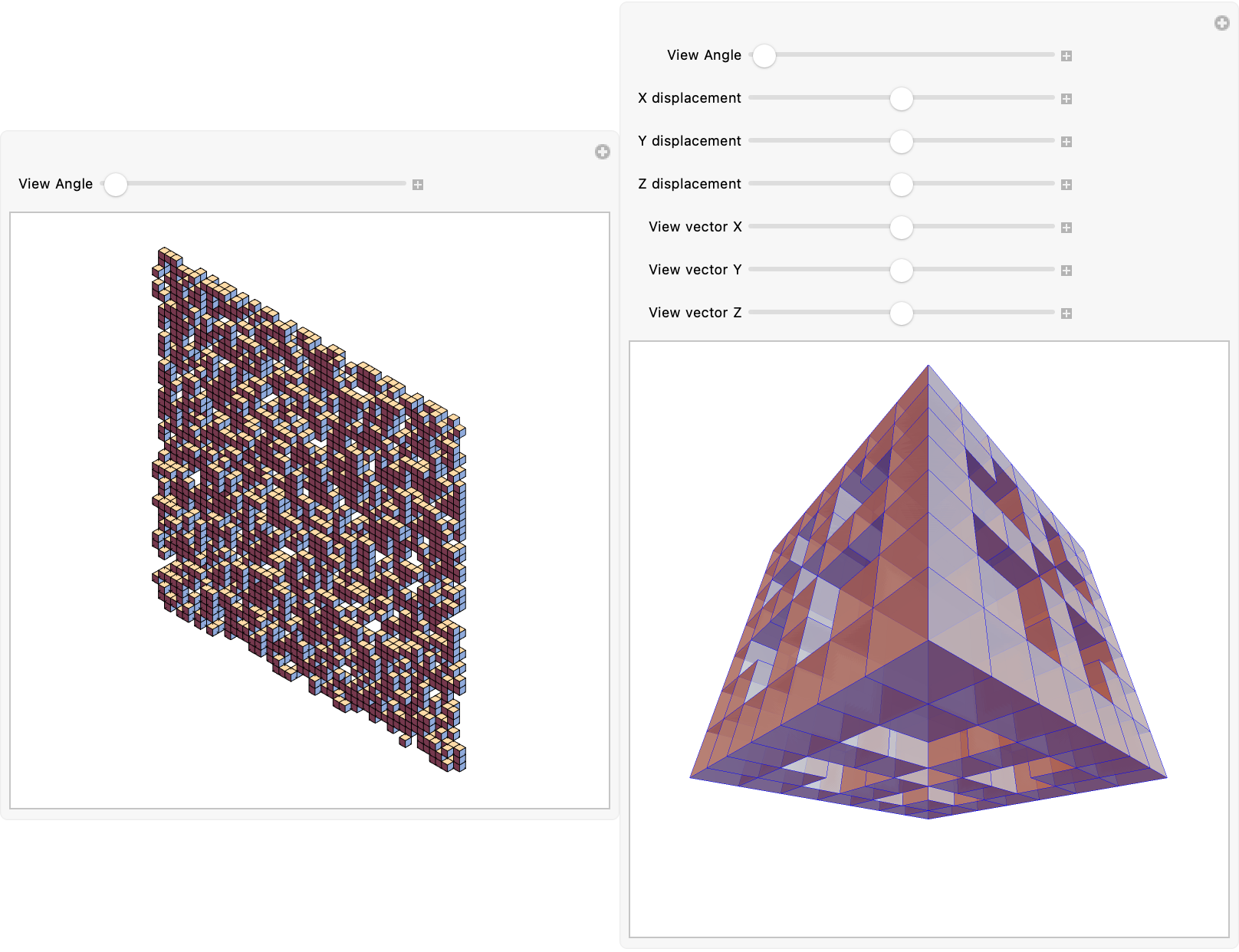
I've always been a fan of 3D stuff whether it's on PDF, animated via Wolfram Language, you name it; these transitions are amazing & the cellular automata are so diverse. What makes a cellular automata good? Every cellular automata has had a different life experience and they say, you should do it this way or that but there's no need anymore this is phenomenal.