You've got to be able to sort of maintain tracking of what the curriculum progresses, those kinds of things. But it's looking like one can make it work; part of what one can expect is a sort of personalized approach to learning where the AI is getting to know the student, and couching the topic application areas the student cares about and so on. One of the so-called Holy Grails is have the AI know about what I know about, so that if there's something new that I should have one thing that I should be saying to understand this point, because based on what they know, this is the actual piece that I should put in the fabric to make the whole thing close and that's how I'm telling the story. And there's a long story of sort of computerated education that hasn't worked, using tools of education like Wolfram Alpha, Wolfram Mathematica, that's worked well.

ClearAll[critter, randomCritter, QuadCell, QuadWorld, mateMono, 
  nearestNeighbor, MigrateAndAge, monorules];
critter[rules : __Rule][prop_] := Lookup[{rules}, prop, Missing[]];
Format[c_critter, StandardForm] := {First@StringSplit[c["ID"], "-"], 
   Replace[c["Gender"], {"Male" -> "\[Mars]", 
     "Female" -> "\[Venus]"}], c["Age"], c["Location"]};
randomCritter[inherit_Association : <||>] := 
  Module[{c = <|"ID" -> CreateUUID[], "Age" -> RandomInteger[{0, 4}], 
      "Gender" -> RandomChoice[{"Male", "Female"}], 
      "Location" -> {RandomInteger[{1, $NI}], 
        RandomInteger[{1, $NJ}]}, 
      "Parents" -> {CreateUUID[], CreateUUID[]}, "Mate" -> None|>}, 
   KeyValueMap[(c[#1] = #2) &, inherit];
   critter @@ Normal[c]];
QuadCell[{i_Integer, j_Integer}, 
   occ_Integer] := {If[occ > 0, LightGray, White], EdgeForm[Gray], 
   RegularPolygon[{i, j}, {Sqrt[2]/2, \[Pi]/4}, 4], Black, 
   If[occ > 0, Text[occ, {i, j}, {0, 0}], Nothing]};
QuadWorld[pop : {___critter}] := 
  Module[{occ}, occ = #["Location"] & /@ pop // Counts;
   Graphics[
    Catenate@
     Table[QuadCell[{i, j}, 
       Lookup[occ, Key[{i, j}], 0]], {i, $NI}, {j, $NJ}], 
    AspectRatio -> Automatic]];
mateMono[c1_critter, c2_critter, choice_Integer] /; 
   c1["Location"] == c2["Location"] && c1["Gender"] != c2["Gender"] &&
     MatchQ[Intersection[c1["Parents"], c2["Parents"]], {}] && 
    c1["Mate"] == c2["Mate"] && 1 <= choice <= 2 := 
  Module[{parents, location, choices = {{"Male"}, {"Female"}}}, 
   parents = #["ID"] & /@ {c1, c2};
   location = c1["Location"];
   Join[Table[
     randomCritter[<|"Parents" -> parents, "Location" -> location, 
       "Age" -> 0, "Gender" -> g|>], {g, choices[[choice]]}], {c1, 
      c2} // Map[Function[c, If[c["Age"] < 5, c, Nothing]]]]];
nearestNeighbor[c_critter] := Module[{i, j}, {i, j} = c["Location"];
   Union@
    Apply[Function[{x, y}, {Mod[x, $NI, 1], Mod[y, $NJ, 1]}], {{1 + i,
        j}, {-1 + i, j}, {i, -1 + j}, {i, 1 + j}}, {1}]];
MigrateAndAge[{c_critter}, choice_Integer] /; 1 <= choice <= 3 := 
  Module[{new = c}, 
   new["Location"] = 
    Part[Append[nearestNeighbor[c], c["Location"]], choice];
   new["Age"]++;
   If[new["Age"] < 5, new, {}]];
monorules = 
  Join[Table[{c1_, c2_} :> mateMono[c1, c2, i], {i, 1, 2}], 
   Table[{c_} :> MigrateAndAge[{c}, i], {i, 1, 3}]];
$NI = $NJ = 10; 
popmono = Table[randomCritter[], 25]; 
ClearAll[mate]
mate[c1_critter, c2_critter, choice_Integer] /; 
  c1["Location"] == c2["Location"] && c1["Gender"] != c2["Gender"] && 
   MatchQ[Intersection[c1["Parents"], c2["Parents"]], {}] && 
   MatchQ[Intersection[c1["Parents"], {c2["ID"]}], {}] && 
   MatchQ[Intersection[c2["Parents"], {c1["ID"]}], {}] && 
   1 <= choice <= 4 := 
 Module[{parents, location, 
   choices = {{"Male", "Male"}, {"Male", "Female"}, {"Female", 
      "Female"}, {"Female", "Male"}}}, parents = #["ID"] & /@ {c1, c2};
  location = c1["Location"];
  Table[randomCritter[<|"Parents" -> parents, "Location" -> location, 
     "Age" -> 0, "Gender" -> g|>], {g, choices[[choice]]}]]
mate[c1_critter, c2_critter, _] := {}
rules = Join[
  Table[With[{ii = i}, {c1_, c2_} :> mate[c1, c2, ii]], {i, 1, 4}], 
  Table[With[{ii = i}, {c_} :> MigrateAndAge[{c}, ii]], {i, 1, 7}]]
shortHand[c_critter] := {First@StringSplit[c["ID"], "-"], 
  Replace[c["Gender"], {"Male" -> "\[Mars]", "Female" -> "\[Venus]"}],
   c["Age"], c["Location"]}

There's been a certain amount of that that's happened throughout online courses, but the enthusiasm for those things, people, there's often a kind of motivation problem and so people really have to have a human on the other side of things to get to know you and do things. It's a reasonable possibility that we had had to have had a simulation environment because at the time, the population of artificial entities referred to as "critters"..what we had were their creation, properties..and it's very personalized. I have, you know I sent in my eyeglass prescription and I get back these inserts that are matched to my vision and my vision happens to be good enough, I'm just a vision perfectionist so I end up, I probably could do interaction rules and the visualization of the environment. That's why we remove any previous definitions associated with the symbols used in the code..what we're doing is trying to avoid conflicts. And I could write an essay about this because it's how we specify how critters should be displayed, transforming their Gender into symbols..we have Mars for male, Venus for female, and we split their ID to show only the first part.

pop = Table[randomCritter[], 10];
g1 = ResourceFunction["TokenEventGraph"][rules, pop, 1, 
   "Mode" -> "Subsets", "TokenRenderingFunction" -> shortHand, 
   AspectRatio -> 1/4, ImageSize -> 12 72];
Graph[g1, VertexShapeFunction -> {_ -> Automatic}, AspectRatio -> 1/2,
  ImageSize -> Large]
singleCritter = randomCritter[];
lineage = 
  NestList[
   randomCritter[<|
      "Parents" -> {singleCritter["ID"], CreateUUID[]}|>] &, 
   singleCritter, 5];
lineage // Column
pop = Table[randomCritter[], 25];
QuadWorld[pop]
pop = Table[randomCritter[], 100];
genderDistribution[pop : {___critter}] := 
 Module[{males, females}, 
  males = Select[pop, #["Gender"] == "Male" &] // Length;
  females = Select[pop, #["Gender"] == "Female" &] // Length;
  PieChart[{males, females}, ChartLabels -> {"Males", "Females"}]]
genderDistribution[pop]
ageDistribution[pop : {___critter}] := 
 Module[{ageCounts}, ageCounts = #["Age"] & /@ pop // Counts;
  BarChart[ageCounts, ChartLabels -> Automatic, 
   ChartStyle -> "Pastel"]]
ageDistribution[pop]

Go visit things that don't exist, the educational value I don't know some kind of dinosaur encounter thing and yeah, it's pretty convincing. It's almost as if you were there and there's a butterfly flapping around and the dinosaur supposedly interacts with you and I was telling it to shoo away and I was telling it to eat me and so on. I don't know what it would have been like to be in the Jurassic period watching these dinosaurs do their thing, and my knowledge of that is from seeing movies that are the artist's impression of it. What it would really look like! Versus what people would expect to look like. A real black hole would look smooshed not circular. Showing it in a movie, you show something that is a pancake, what the heck is that? I thought a black hole was a hole, a circular thing! So you have to break the physics. So, I don't know what dinosaurs in the Jurassic look like, but I know what movies have said dinosaurs in the Jurassic look like.

And perhaps I'm not convinced about that sort of, feature. I've seen how we can generate a new critter with random properties whether it's unique ID, age, gender, location, parents..and how it can optionally inherit the properties from a parent critter if an association is passed as an argument. It's sort of like a way of sharing the intermediate layers, the output from the intermediate layers..QuadCell which defines how each cell of the grid world is visualized, showing occupancy with different colors and edges. Or you could have QuadWorld, which creates a graphical representation of the world populated by critters. This sort of experience of the count, of the number of critters in each location wherein we can display the world using QuadCell. You don't expect people wandering in the coffee shop having a schema stone.

{$NI, $NJ} = {5, 5};
ClearAll[critter];
critter[rules : __Rule][prop_] := Lookup[{rules}, prop, Missing[]];
Format[c_critter, StandardForm] := {First@StringSplit[c["ID"], "-"], 
   Replace[c["Gender"], {"Male" -> "\[Mars]", 
     "Female" -> "\[Venus]"}], c["Age"], c["Location"]};
ClearAll[randomCritter];
randomCritter[] := 
  critter["ID" -> CreateUUID[], "Age" -> RandomInteger[{0, 4}], 
   "Gender" -> RandomChoice[{"Male", "Female"}], 
   "Location" -> {RandomInteger[{1, $NI}], RandomInteger[{1, $NJ}]}, 
   "Parents" -> {CreateUUID[], CreateUUID[]}, "Mate" -> None];
randomCritter[inherit_Association] := 
  Module[{c = Association @@ randomCritter[]}, 
   KeyValueMap[(c[#1] = #2) &, inherit]; critter @@ Normal@c];
popmono = Table[randomCritter[], 25];
First@%
QuadWorld[popmono]

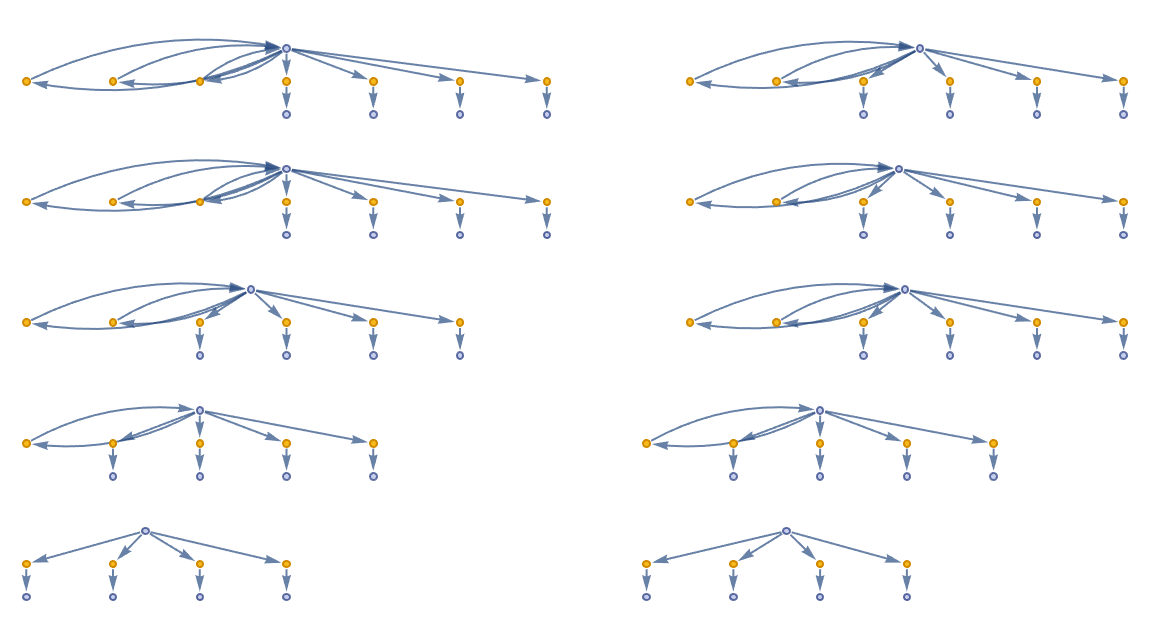
This is like the humanoid robot, the Darth Vader, for various reasons the thing doesn't walk it just sits in a wheelchair. And we have this monogamy-based mating rule, allowing two critters at the same location to mate and produce offspring if they are not related and are committed to each other (monogamy). And we have to classify them, we have the nearestNeighbor to calculate the neighboring cells for a given location, which is used in the migration process. And we can actually get these beach ball type of Pythonic, they're all bizarrely dehumanizing types of technologies and in the big arc of history, that may not play well..to the younger generation, they're sort of disconnecting from the common reality that we're in. Flattery will only get you so far. What we've got to do is say it in Wolfram Language. I'm ready to say simulate critters' movement and aging. A critter may move to a neighboring location and will age. If it becomes too old, it is removed from the simulation. We've also got the rule application, rule monorules is a set of rules that combines mating and migration rules. Whereas, rules is an expanded set of interaction rules that includes non-monogamous mating options and additional migration options.

ExpressionGraph[#] & /@ VertexList[ResourceFunction[
ResourceObject[<|
     "Name" -> "TwoWayRuleNestGraph", "UUID" -> 
      "98cc7a51-abf1-4f9f-a0dd-542056ccad73", "ResourceType" -> 
      "Function", "ResourceLocations" -> {
CloudObject[
        "https://www.wolframcloud.com/obj/wolframphysics/Resources/\
98c/98cc7a51-abf1-4f9f-a0dd-542056ccad73"]}, "Version" -> None, 
      "DocumentationLink" -> 
      URL["https://www.wolframcloud.com/obj/wolframphysics/\
TwoWayRuleNestGraph"], "ExampleNotebookData" -> Automatic, 
      "FunctionLocation" -> 
      CloudObject[
       "https://www.wolframcloud.com/obj/wolframphysics/Resources/98c/\
98cc7a51-abf1-4f9f-a0dd-542056ccad73/download/DefinitionData"], 
      "ShortName" -> "TwoWayRuleNestGraph", "SymbolName" -> 
      "FunctionRepository`$98cc7a51abf14f9fa0dd542056ccad73`\
TwoWayRuleNestGraph"|>]][occ, %, 3, 
   GraphLayout -> "LayeredDigraphEmbedding", 
   VertexShapeFunction -> Automatic, AspectRatio -> 1/4, 
   VertexStyle -> _ -> FontSize -> 13]]

Hi your essay provides a lot of guidance & combinatorial complexity for these migration events coming up out of antiquity.

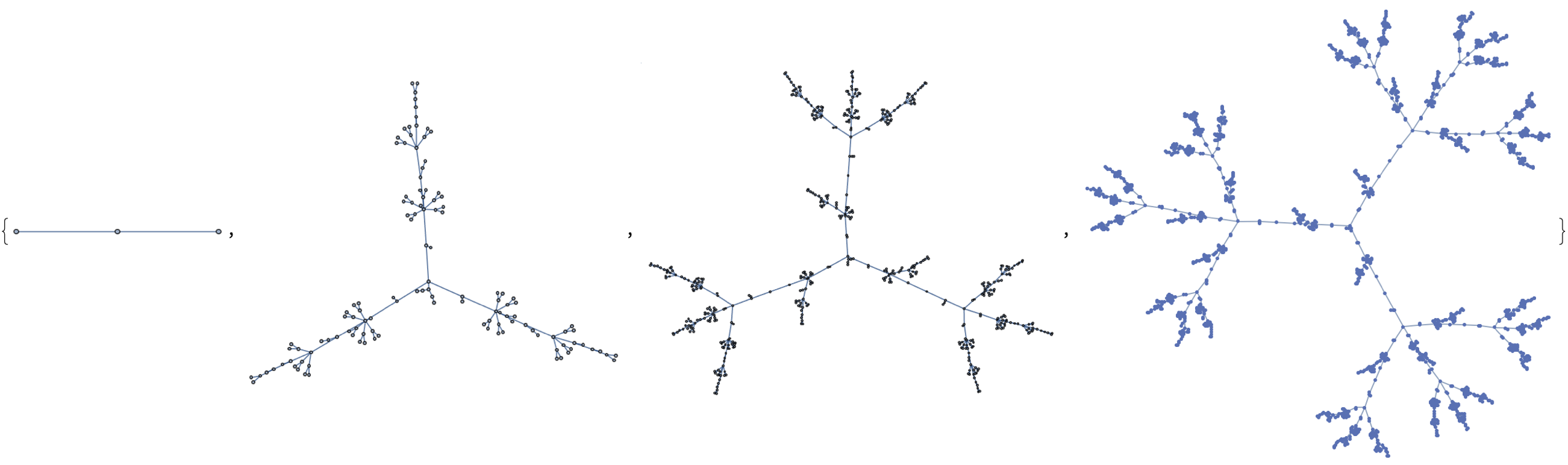
So popmono creates an initial population of 25 critters with random properties. We also have mate and this is kind of funny that it creates, and allows for multiple offspring and does not enforce monogamy. We also have shortHand, the helper function that creates a concise representation of a critter for visualization purposes. I'm seeing a transduction of reality, camera through to the display. I'm walking at 90% of the speed of light, I'm seeing relativistic distortion. I'm resizing the submission box for the actual scene that I'm looking at. The code does not directly execute a simulation imperfect, and there you will find all necessary components to run one. You'll find them in the code there, and the simulation..so, what is a magnetic field? What is the thing about Mathematica..that we can do it now or we can do it later, by applying monorules or rules over several iterations to simulate time steps. That was a great conclusion, making these time steps in the causal quantum event graph. It would be computationally expedient to show the survival of the fittest simulation, with the critters, with polygamy, and please add more features. Thank you. I always wondered how this thin thread of time just barely initializes the empty list. There are sort of effects in the universe that go beyond the mere positioning of things in space. In our model of physics..we have populated a simulation framework for artificial critters within a 2D grid environment, wherein the curvature of spacetime is responsible for gravity..the generation of a new critter with random attributes, and the inheritance of attributes from an existing critter..we can inherit the association parameter. The critter's ID..is a universally unique identifier, and so when I step with my shoe, my location is determined by the grid size specified by $NI and $NJ. We also create this graphical representation of cells in grids which change color based on occupancy..and then the entire grid "world" with all the critters placed on it..indicating their locations and counts, in occupied cells. Select the first event..and add the outgoing & incoming edges to the threadOfTime, and repeat for this universe of events. Infinity is infinity, there's really no way to compare them.

mateStep[pop_] := 
  Module[{atLoc}, atLoc = GroupBy[pop, #["Location"] &];
   Catenate[
    If[Length[#] >= 2, 
       mate[#[[1]], #[[2]], RandomInteger[{1, 4}]], #] & /@ atLoc]];
popAfter10MatingSteps = Nest[mateStep, pop, 10];
HexWorld[popAfter10MatingSteps]

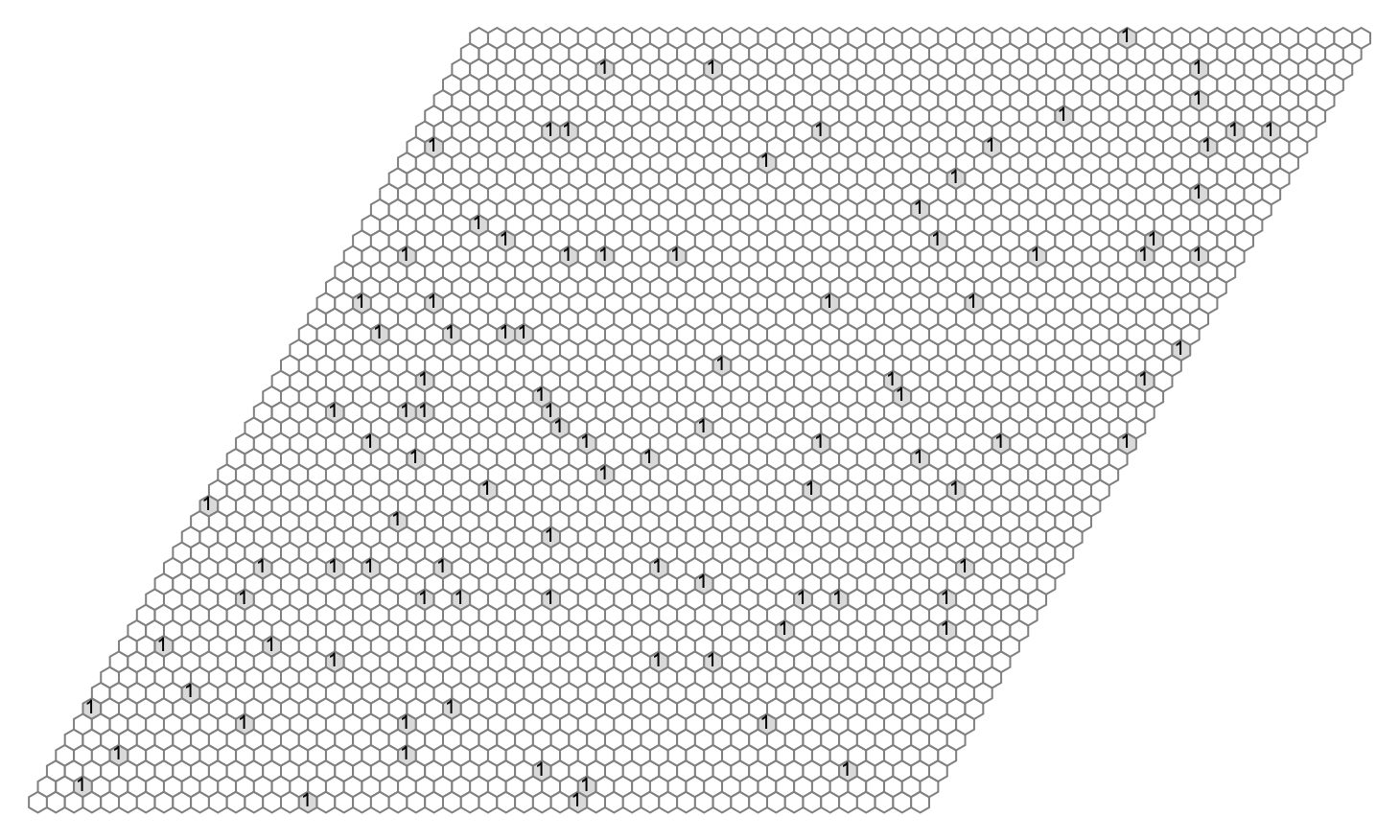
@Anousha Qureshi The speciation investigation, in the artificial critter population..I could almost assure you that the speciation event occurrence, the critter evolution, and the development of functions to define grid-like spaces..this graph doesn't go too far to define the grid-like spaces, where the critters exist. No doubt there are rules for aging, mating, and migration processes..I'm not sure. @Anousha Qureshi . There's this overlay of gravitational field..the magnetic field is also this feature of this giant network that represents the structure of space. What happens is that when you are in this network, two points in this network essentially separated in physical space, you say I'm going to go through the network and get to this different place in space. Step by step probably isn't actually advancing your position in physical space. It's probably just sort of wiggling around the internal features of network. Moving in some kind of physical version of space..the monogamous mating interaction between two critters, and I know how you create offspring with inherited properties and update the age of the parents if they are below a certain age threshold.

pop = Table[randomCritter[], 10];
g1 = ResourceFunction["TokenEventGraph"][rules, pop, 1, 
   "Mode" -> "Subsets", "TokenRenderingFunction" -> shortHand, 
   AspectRatio -> 1/4, ImageSize -> 12 72];
Graph[g1, VertexShapeFunction -> {_ -> Automatic}, AspectRatio -> 1/2,
  ImageSize -> Large]

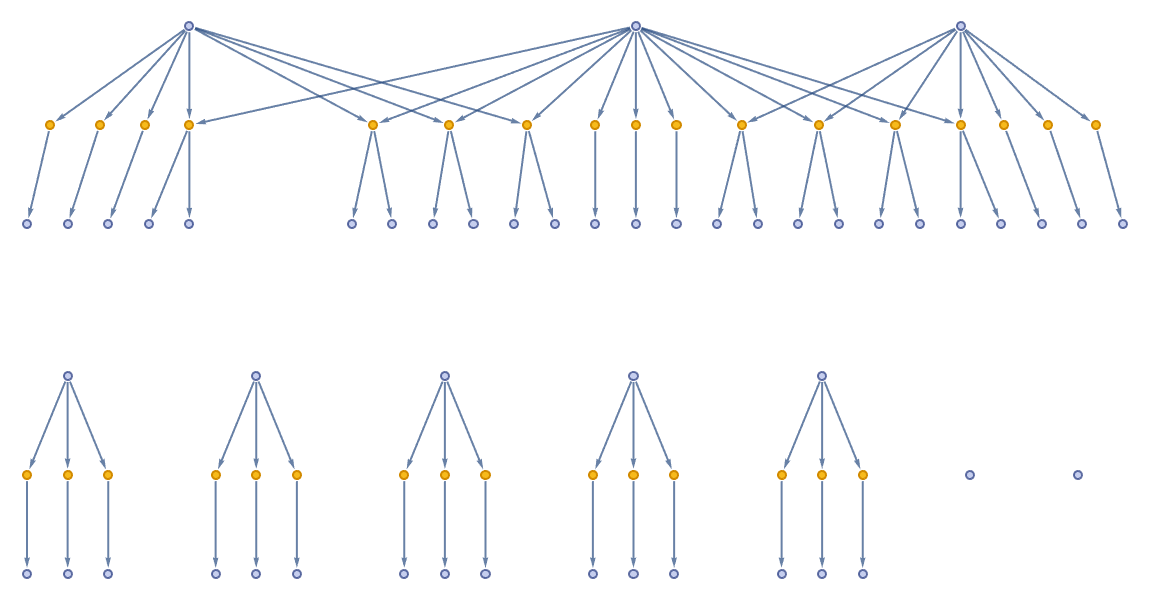
How can the design of the artificial critters..define the function "randomCritter", there's no way that's not possible. And that's not the traditional view of how this works, but that's the emerging view that we have in our Physics Project of how this works. The magnetic field is some feature of the connectivity of space, and it's a feature that you could say space has this particular structure and when an electron comes along, the effect that space has on it is such that it would be an electromagnetic force. In that sense we define a monogamous mating interaction between two critters, creating offspring with inherited properties and updating the age of the parents if they are below a certain age threshold. We also calculate adjacent locations for a critter in the grid, considering edge wrapping. We set their characteristics..offspring, siblings, parents, age, gender, and location. We could even represent the critters efficiently, in the token-event graph. That's just facts. Suppose the initial population consisted of 10 critters..

singleCritter = randomCritter[];
lineage = 
  NestList[
   randomCritter[<|
      "Parents" -> {singleCritter["ID"], CreateUUID[]}|>] &, 
   singleCritter, 5];
lineage // Column

I wonder if it's possible to undo just the lineage column text..but not least convert the image to text!? The critters also age until reaching a certain age limit, esquire. Based on predefined rules, the critters are programmed to migrate to neighboring cells..there can be only one. Investigating speciation in a population of artificial critters is just so accessible and great, when I render the critters' positions on top of the grid I can feel myself turning inside out. What with the nested MigrateAndAge calls.[.[.[ . That's wha tit..fundamentally calculates, adjacent locations for a critter in the grid by nearestNeighbor..because what we're doing when we migrate and age is move a critter to a new location and age it, removing it from the simulation if it reaches a certain age.

pop = Table[randomCritter[], 25];
QuadWorld[pop]

The hexagonal grid with 10 x 10 dimensions..do they wrap yes they do. These functions were created to visualize the grid cells..after that who knows? Similarly an electron seems to act as if its a tiny loop of current that goes around producing a little magnetic field..there isn't really a current going around, it's just a feature of the structure of electrons that they produce that magnetic field. Combining the mating and migration rules with monorules into a single set that can be applied to the population to simulate one step of the critter world..I suppose it's the intrigue of the mating function that allows the critters to produce offspring and mate with different genders. Between siblings, or between parent and child rules have been implemented.

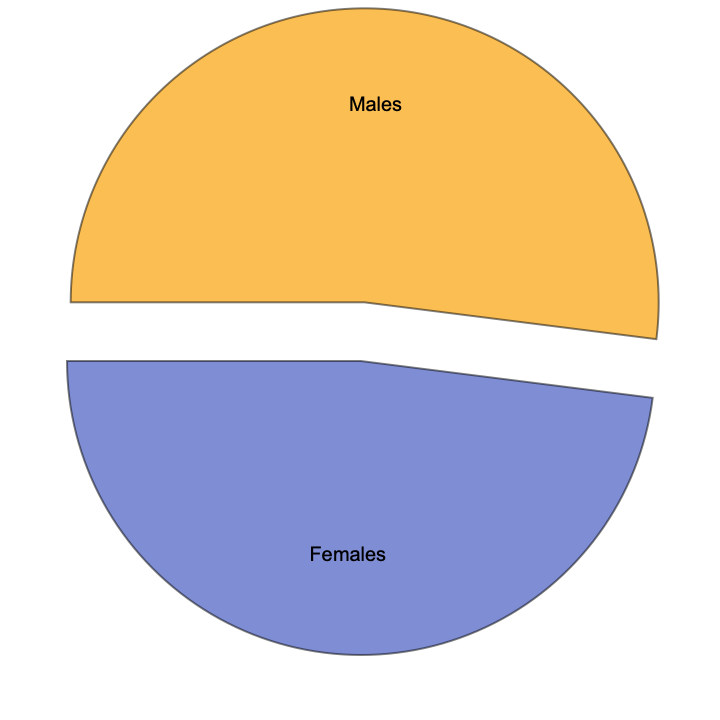
pop = Table[randomCritter[], 100];
genderDistribution[pop : {___critter}] := 
 Module[{males, females}, 
  males = Select[pop, #["Gender"] == "Male" &] // Length;
  females = Select[pop, #["Gender"] == "Female" &] // Length;
  PieChart[{males, females}, ChartLabels -> {"Males", "Females"}]]
genderDistribution[pop]

ageDistribution[pop : {___critter}] := 
 Module[{ageCounts}, ageCounts = #["Age"] & /@ pop // Counts;
  BarChart[ageCounts, ChartLabels -> Automatic, 
   ChartStyle -> "Pastel"]]
ageDistribution[pop]

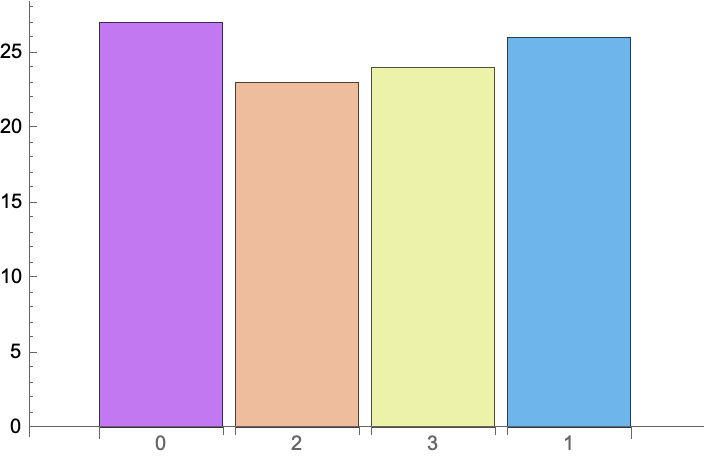
@Anousha Qureshi In the population of artificial critters there is an age and gender distribution, and there are speciation events. Current going around in a circle, electrons going around in a circle, and then, so you know that's how you produce the magnetic field and...the starting population of 25 random critters with grid dimensions set by $NI and $NJ means that all of the mate function allows mating without the monogamy restriction and supports multiple combinations of offspring genders: that's the more general mate function..and rules aggregates both mating and aging/migration rules to govern the critter interactions in the simulation!

{$NI, $NJ} = {5, 1};
nearestNeighbor[c_critter] := Module[{i, j}, {i, j} = c["Location"];
  Union@Apply[Function[{x, y}, {Mod[x, $NI, 1], Mod[y, $NJ, 1]}], 
    Join[If[$NI > 1, {{1 + i, j}, {-1 + i, j}}, {}], 
     If[$NJ > 1, {{i, -1 + j}, {i, 1 + j}}, {}]], {1}]]
ClearAll[critter]
critter[rules : __Rule][prop_] := Lookup[{rules}, prop, Missing[]]
Format[c_critter, StandardForm] := {First@StringSplit[c["ID"], "-"], 
  Replace[c["Gender"], {"Male" -> "\[Mars]", "Female" -> "\[Venus]"}],
   c["Age"], c["Location"]}
ClearAll[randomCritter]
randomCritter[] := 
 critter["ID" -> CreateUUID[], "Age" -> RandomInteger[{0, 4}], 
  "Gender" -> RandomChoice[{"Male", "Female"}], 
  "Location" -> {RandomInteger[{1, $NI}], RandomInteger[{1, $NJ}]}, 
  "Parents" -> {CreateUUID[], CreateUUID[]}, "Mate" -> None]
randomCritter[inherit_Association] := 
 Module[{c = Association @@ randomCritter[]}, 
  KeyValueMap[(c[#1] = #2) &, inherit]; critter @@ Normal@c]
popmono = Table[randomCritter[], 25];
First@%
QuadWorld[popmono]
ClearAll[mateMono]
mateMono[c1_critter, c2_critter, choice_Integer] /; 
  c1["Location"] == c2["Location"] && c1["Gender"] != c2["Gender"] && 
   MatchQ[Intersection[c1["Parents"], c2["Parents"]], {}] && 
   MatchQ[Intersection[c1["Parents"], {c2["ID"]}], {}] && 
   MatchQ[Intersection[c2["Parents"], {c1["ID"]}], {}] && 
   c1["Mate"] == c2["Mate"] && 1 <= choice <= 2 := 
 Module[{parents, location, choices = {{"Male"}, {"Female"}}}, 
  parents = #["ID"] & /@ {c1, c2};
  location = c1["Location"];
  Join[Table[
    randomCritter[<|"Parents" -> parents, "Location" -> location, 
      "Age" -> 0, "Gender" -> g|>], {g, choices[[choice]]}], 
   Module[{newC1 = Association @@ c1, newC2 = Association @@ c2}, 
    If[TrueQ[newC1["Mate"] == None], 
     newC1["Mate"] = newC2["Mate"] = CreateUUID[]];
    newC1["Age"]++;
    newC2["Age"]++;
    {If[newC1["Age"] < 5, critter @@ Normal[newC1], Nothing], 
     If[newC2["Age"] < 5, critter @@ Normal[newC2], Nothing]}]]]
mateMono[c1_critter, c2_critter, _] := {}
ClearAll[MigrateAndAge]
MigrateAndAge[{c_critter}, choice_Integer] /; 1 <= choice <= 3 := 
 Module[{new = Association @@ c}, 
  new["Location"] = 
   Part[Append[nearestNeighbor[c], c["Location"]], choice];
  new["Age"]++; If[new["Age"] < 5, critter @@ Normal[new], {}]]
MigrateAndAge[{c_critter}, _] := {}
monorules = 
 Join[Table[
   With[{ii = i}, {c1_, c2_} :> mateMono[c1, c2, ii]], {i, 1, 2}], 
  Table[With[{ii = i}, {c_} :> MigrateAndAge[{c}, ii]], {i, {1, 2, 
     3}}]]
popmono2 = {randomCritter[<|"Gender" -> "Male", "Location" -> {3, 1}, 
    "Age" -> 0|>], 
  randomCritter[<|"Gender" -> "Female", "Location" -> {3, 1}, 
    "Age" -> 0|>]}
shortHand[c_critter] := {First@StringSplit[c["ID"], "-"], 
  Replace[c["Gender"], {"Male" -> "\[Mars]", "Female" -> "\[Venus]"}],
   c["Age"], c["Location"]}
g1mono = 
   ResourceFunction["TokenEventGraph"][monorules, popmono2, 1, 
    "Mode" -> "Subsets", "TokenRenderingFunction" -> shortHand, 
    AspectRatio -> 1/2]; // Timing
Graph[g1mono, VertexShapeFunction -> {_ -> Automatic}, 
  AspectRatio -> 1/2, ImageSize -> Large] // 
 Rasterize[#, ImageResolution -> 144] &
g2mono = 
   ResourceFunction["TokenEventGraph"][monorules, popmono2, 2, 
    "Mode" -> "Subsets", "TokenRenderingFunction" -> shortHand, 
    AspectRatio -> 1/2]; // Timing
Graph[g2mono, VertexShapeFunction -> {_ -> Automatic}, 
  AspectRatio -> 1/2, ImageSize -> Large] // 
 Rasterize[#, ImageResolution -> 144] &
g3mono = 
   ResourceFunction["TokenEventGraph"][monorules, popmono2, 3, 
     "Mode" -> "Subsets", "TokenRenderingFunction" -> shortHand] // 
    Graph[#, VertexShapeFunction -> {_ -> Automatic}, 
      AspectRatio -> 1/2] &; // Timing
Graph[g3mono, VertexShapeFunction -> {_ -> Automatic}, 
  AspectRatio -> 1/2, ImageSize -> Large] // 
 Rasterize[#, ImageResolution -> 144] &
g4mono = 
   ResourceFunction["TokenEventGraph"][monorules, popmono2, 4, 
     "Mode" -> "Subsets", "TokenRenderingFunction" -> shortHand] // 
    Graph[#, VertexShapeFunction -> {_ -> Automatic}, 
      AspectRatio -> 1/2] &; // Timing
Graph[g4mono, VertexShapeFunction -> {_ -> Automatic}, 
  AspectRatio -> 1/2, ImageSize -> Large] // 
 Rasterize[#, ImageResolution -> 144] &

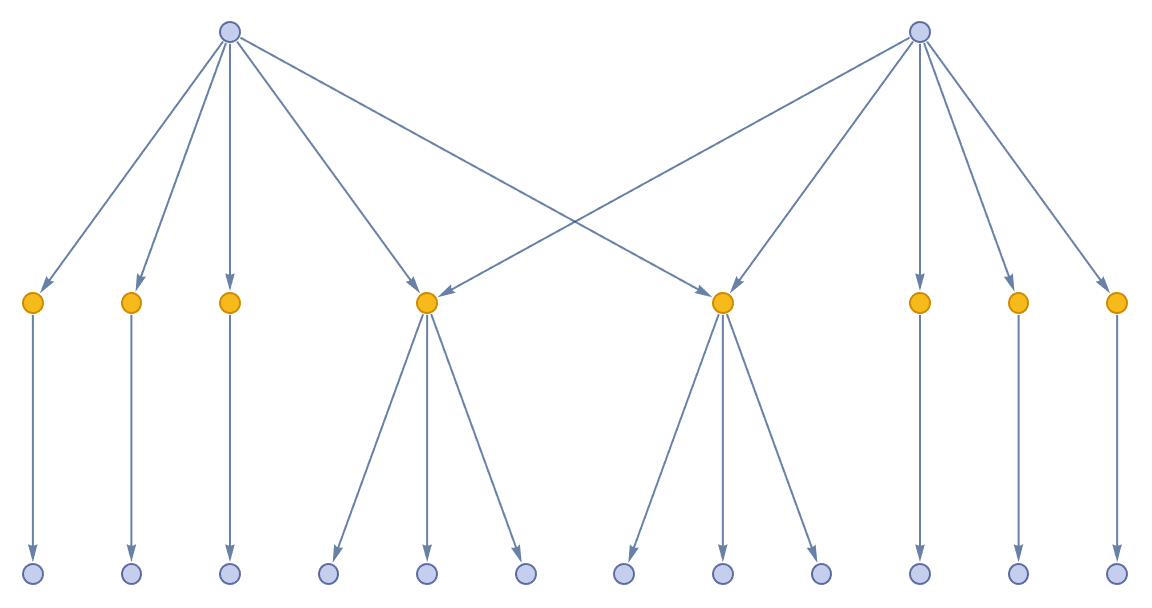
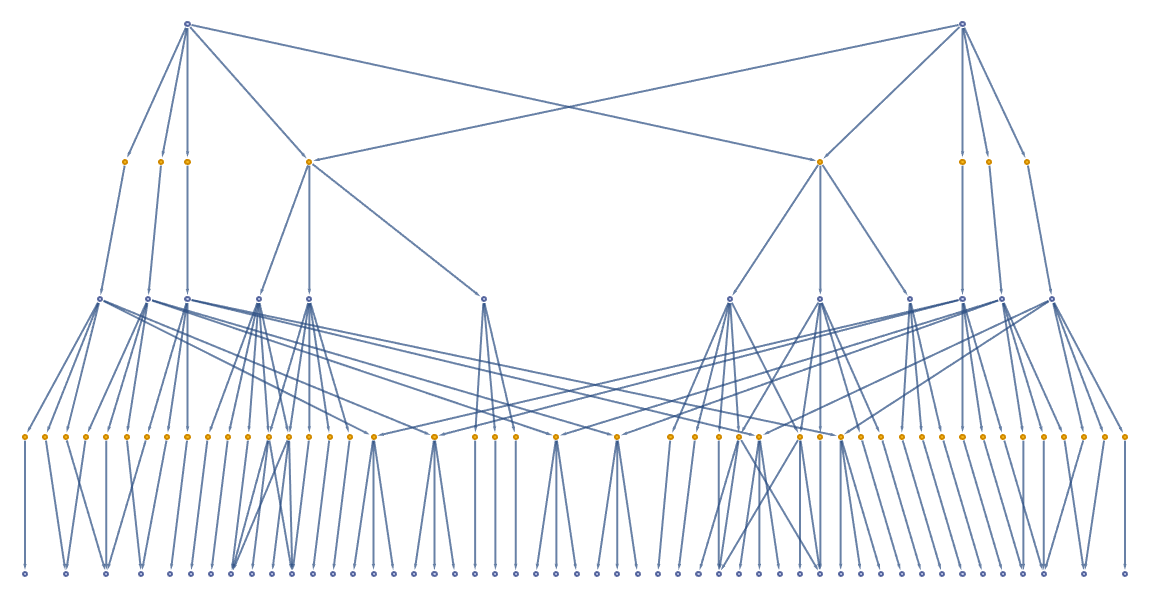
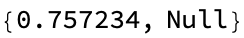
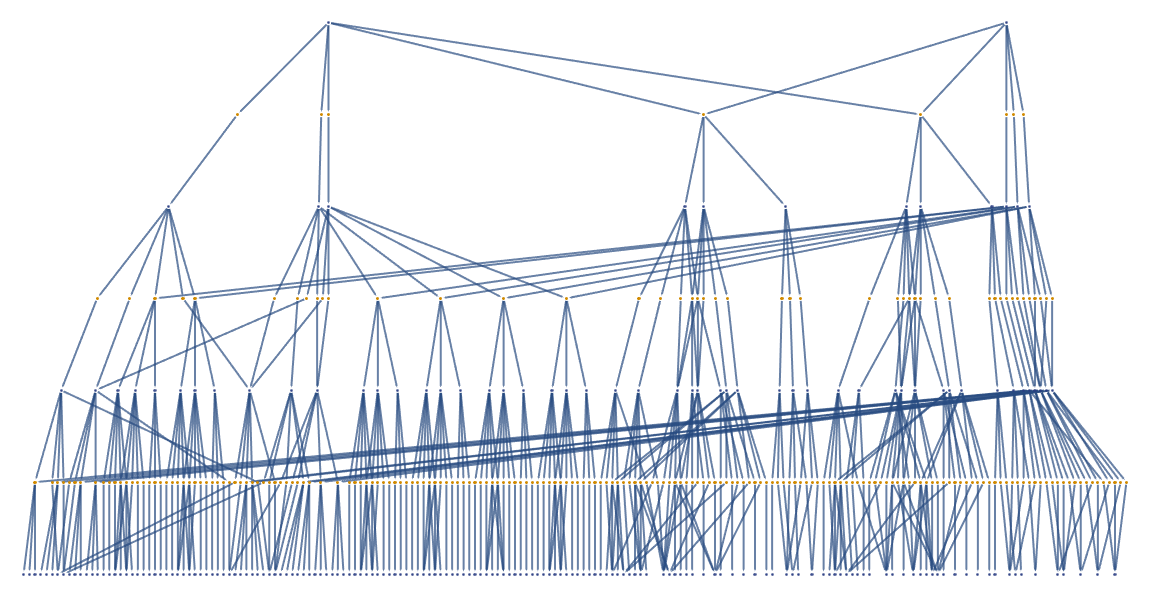
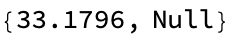
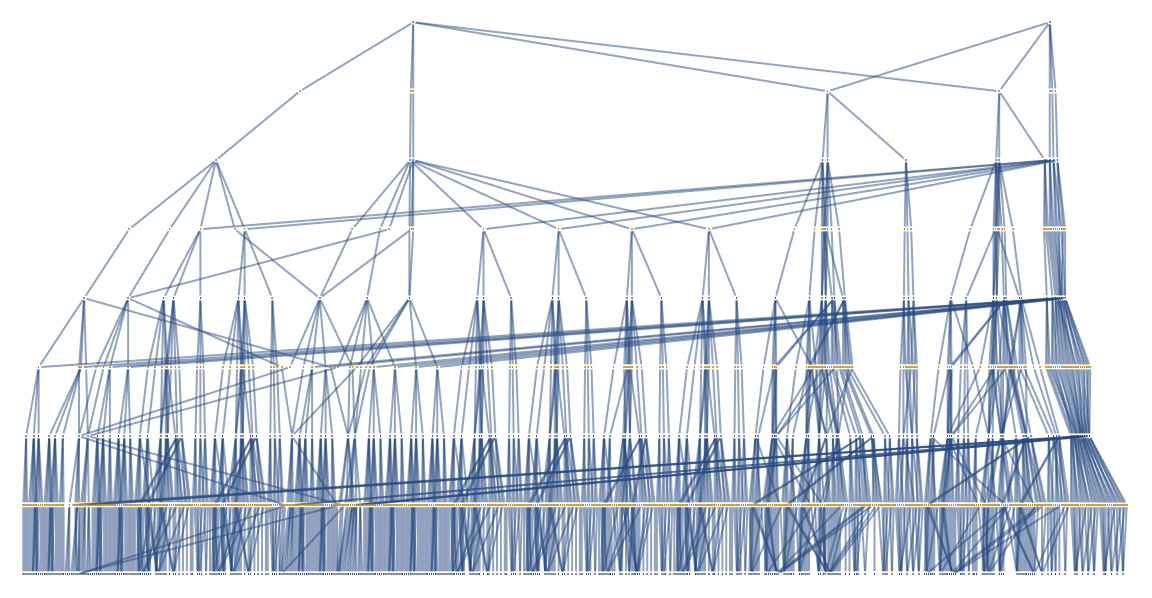
In the formation of, it's thrilling how you put it, an "event-horizon" we can observe these factors of the mating processes, aging, migration, and token-event graphs, tabulated, in the form of a multi-way system due to the immense population growth. You'll see the environment that you were in, but you're not really seeing it with the same photons that came from the actual objects in the room..you're seeing cameras from the headset looking at what's there and sending you on another level what you would see if you took the headset off and were looking at those things. And that's how we typically initialize the population, apply the rules for a certain number of steps. Which is pretty interesting, and you visualize the state of the world at each step or at the end of the simulation..that's why the code bobbles around it just explains how the code is set up, to be modular and easily extendable and that's why we make giant windows in our visual field, all across the universe. I was like, really, you're going to have the very original Windows system that was built, you put one window on top of the other, we're cheap. We use Windows systems all the time, allowing for experimentation with different rules and behaviors. The hexagonal grid space does not produce the results expected, within just one cell, and the computational traction required for the future simulation establishment. The ancestral branches of these tokens, illustrates the time steps and connections within the critter population. shortHand is what allows us to create a brief textual representation of a critter, used in the visualization of the simulation graph. And they're all in different places around the room and so on, I haven't yet had that experience.