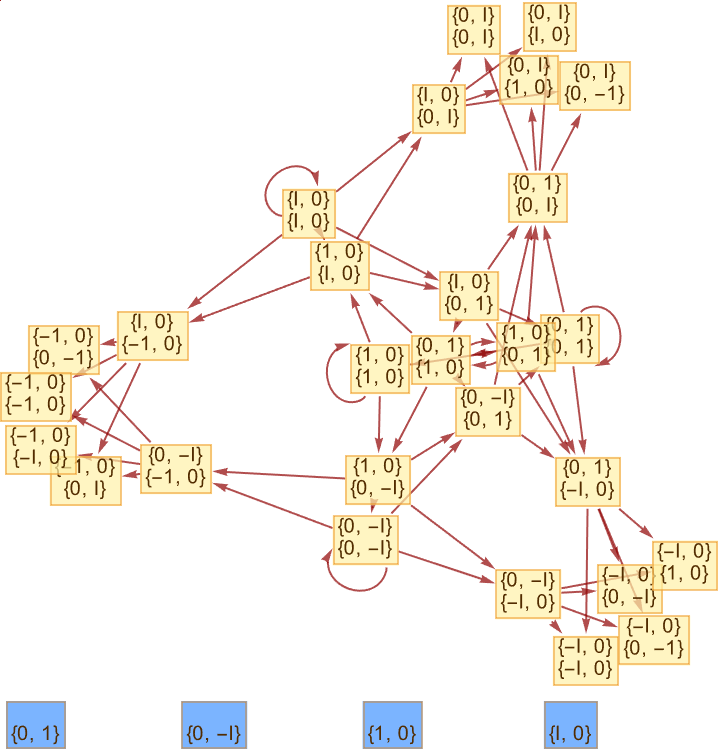
So like you suggest @Mark Merner we can provide a more general description of entanglement, than the classical. It could be the case that we would make up these axioms and every time we wanted to conclude something about mathematics we'd have to go down and be grunging around at the axiomatic level, that's not how mathematics actually works. The Bell test it's our experiment, it's our test of the predictions of quantum mechanics @Mark Merner against those of local realism, considering the possible configurations and variations of the QuantumToMultiwaySystem. I'm free to go over the mystical, this is so exciting! Consider the following. We certainly made it to measure the physical correlates of multiway diagrams, and the experimental mathematical axioms exist such that if we chose them then we wouldn't have a coherent view of mathematics; mathematics would kind of get shredded.

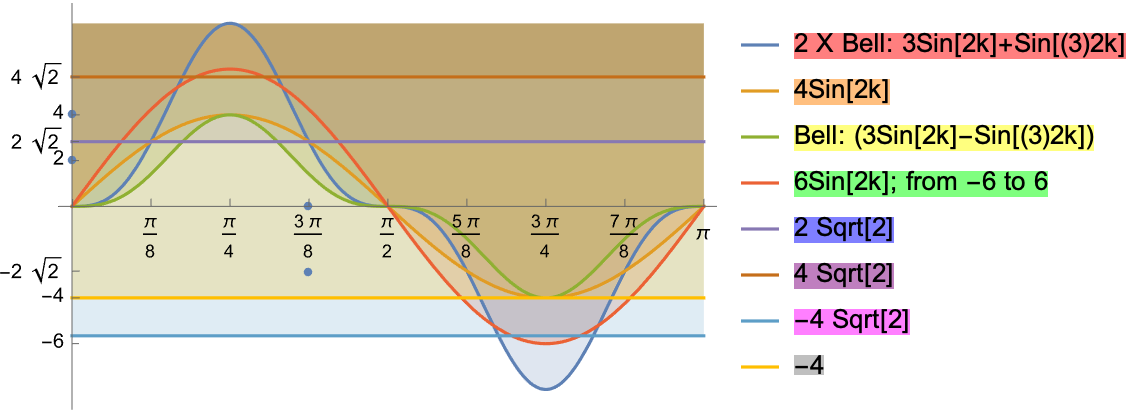
data = {{0, 2}, {0, 4}, {3 Pi/8, 0}, {3 Pi/8, -2 Sqrt[2]}};
plotData = {2 (3 Sin[2 k] - Sin[3*2 k]),
   4 Sin[2 k], 3 Sin[2 k] - Sin[3*2 k],
   6 Sin[2 k], 2 Sqrt[2], 4 Sqrt[2], -4 Sqrt[2], -4};
plotLegend = {Style["2 X Bell: 3Sin[2k]+Sin[(3)2k]", 
    Background -> RGBColor[1, 0, 0, 0.5]],
   Style["4Sin[2k]", Background -> RGBColor[1, 0.5, 0, 0.5]],
   Style["Bell: (3Sin[2k]-Sin[(3)2k])", 
    Background -> RGBColor[1, 1, 0, 0.5]],
   Style["6Sin[2k]; from -6 to 6", 
    Background -> RGBColor[0, 1, 0, 0.5]],
   Style["2 Sqrt[2]", Background -> RGBColor[0, 0, 1, 0.5]],
   Style["4 Sqrt[2]", Background -> RGBColor[0.5, 0, 0.5, 0.5]],
   Style["-4 Sqrt[2]", Background -> RGBColor[1, 0, 1, 0.5]],
   Style["-4", Background -> RGBColor[0.5, 0.5, 0.5, 0.5]] };
plot = Show[
  Plot[plotData, {k, 0, Pi}, Filling -> Top, 
   PlotLegends -> plotLegend],
  ListPlot[data],
  Ticks -> {{0.001 Pi, Pi/8, Pi/4,
     3 Pi/8, Pi/2, 5 Pi/8,
     6 Pi/8, 7 Pi/8, Pi},
    {4 Sqrt[2], 2, 4, 2 Sqrt[2],
     -2 Sqrt[2], -4, -6}}]
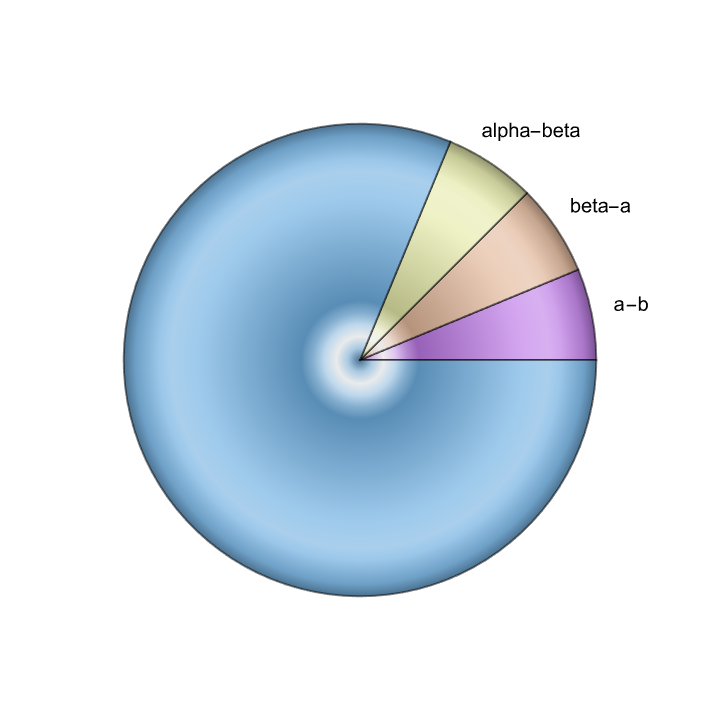
alpha = 3 Pi/8;
beta = Pi/4;
a = Pi/8;
b = 0;
pieChart = PieChart[
  {22.5, 22.5, 22.5, 292.5},
  ChartLabels -> 
   Placed[{"a-b", "beta-a", "alpha-beta"}, "RadialOutside"],
  SectorOrigin -> 0,
  ChartElementFunction -> "GlassSector",
  ChartStyle -> "Pastel"]
Manipulate[ClearAll[data, grid, diffNames, cosValues, S];
 data = {{0, 2}, {0, 4}, {alpha, 0}, {alpha, -2 Sqrt[2]}};
 diffNames = {alpha - beta, alpha - b, a - b, a - beta};
 cosValues = {-Cos[2 (alpha - beta)], +Cos[2 (alpha - b)], -Cos[
     2 (a - b)], -Cos[2 (a - beta)]};
 S = Plus[-Cos[2 (alpha - beta)], +Cos[2 (alpha - b)], -Cos[
     2*a - b], -Cos[2*(a - beta)]];
 grid = Grid[
   {{"Polarizer Angle Names", alpha, beta, a, b, ""},
    {"Polarizer Angle Values", alpha, beta, a, b},
    {"Diff Names", Sequence @@ diffNames, ""},
    {"DiffValues", Sequence @@ cosValues, S},
    {"Solutions for -2 Sqrt[2]", "k = 3Pi/8"}},
   Background -> Hue[0.33, 1, 1, .1],
   Frame -> All],
 {alpha, 3 Pi/8, "alpha", 0, 2 Pi},
 {beta, Pi/4, "beta", 0, 2 Pi},
 {a, Pi/8, "a", 0, 2 Pi},
 {b, 0, "b", 0, 2 Pi}]

There will be constraints, there may even be constraints we're seeing right now. There's a higher level experience of mathematics, it's kind of like we can experience not the molecules bouncing around in the room but the air currents. I love your color scheme and writing style let's steal some inspiration from the throes of your workflow.

operator1 = {{1 + I, 1 - I}, {1 - I, 1 + I}};
operator2 = {{0, 1}, {1, 0}};
basis = {{1, 0}, {0, 1}};
initialState1 = {1 + I, 1 - I};
initialState2 = {0, 1};
steps = 3;
QuantumToMultiwaySystem[<|"Operator" -> operator1, 
  "Basis" -> basis|>, initialState1, steps, "StatesGraph", 
 "StateRenderingFunction" -> (RGBColor[RandomReal[], RandomReal[], 
     RandomReal[]] &)]
QuantumToMultiwaySystem[<|"Operator" -> operator1, 
  "Basis" -> basis|>, initialState1, steps, "CausalGraphInstances", 
 "MaxItems" -> 5]
QuantumToMultiwaySystem[<|"Operator" -> operator1, 
  "Basis" -> basis|>, initialState1, steps, "BranchPairsList", 
 "GivePredecessors" -> True]
Table[QuantumToMultiwaySystem[<|"Operator" -> operator1, 
   "Basis" -> basis|>, initialState1, i, "StatesGraph"], {i, 0, 3}]
QuantumToMultiwaySystem[<|"Operator" -> operator2, 
  "Basis" -> basis|>, initialState2, steps]
QuantumToMultiwaySystem[<|"Operator" -> operator2, 
  "Basis" -> basis|>, initialState2, steps, "PredecessorRulesList"]
QuantumToMultiwaySystem[<|"Operator" -> operator2, 
  "Basis" -> basis|>, initialState2, steps, "EvolutionGraphWeighted"]
QuantumToMultiwaySystem[<|"Operator" -> operator2, 
  "Basis" -> basis|>, initialState2, steps, "StateWeights"]
QuantumToMultiwaySystem[<|"Operator" -> operator2, 
  "Basis" -> basis|>, initialState2, steps, 
 "IncludeStepNumber" -> True, "IncludeStateID" -> True]
QuantumToMultiwaySystem[<|"Operator" -> operator2, 
  "Basis" -> basis|>, initialState2, steps, "LineThickness" -> 2]

This photon polarization coincidence measurement reveals the distinct stages, between four or more detector pairs..it reminds me of that Crab Nebula in 1054, that was kind of hard to miss; there could be a supernova next week and we wouldn't know it. If we look at other galaxies we certainly see supernovas. But we can describe them in terms of simplicity and performance improvement because we've got the entanglement operators now. We can experience not the low-level sub-axiomatic foundations, but instead this kind of higher-level aesthetic thing that is the level that mathematicians typically experience things at. To what extent can we just go off and pick mathematics at random? @Mark Merner . These simulations of various experiments is like when William was going to England and when Halley was a statesman in the late 1600s, and that comet was named after him and one of those things that was of great interest was to explain them, how do orbits work?

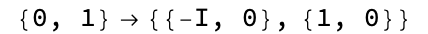
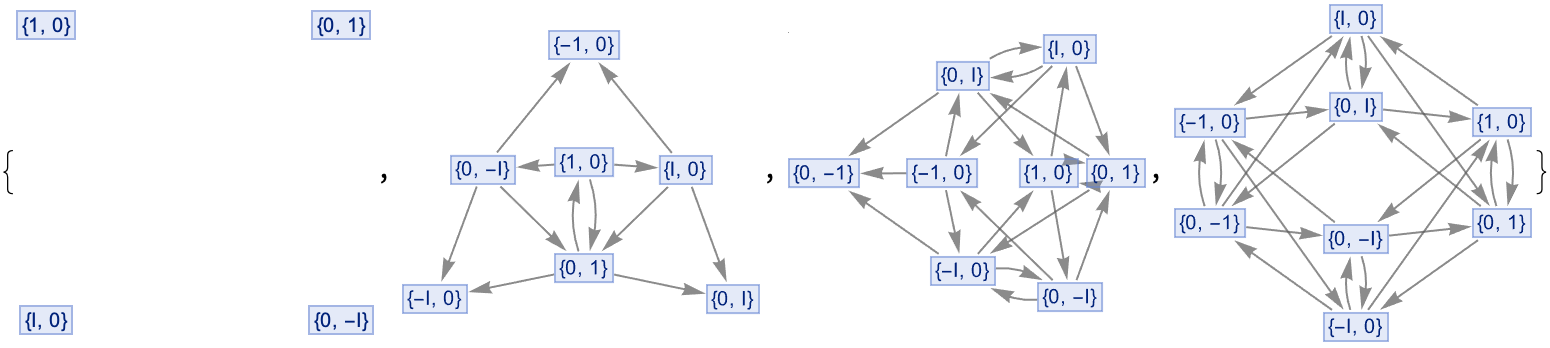
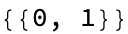
These simulations could inform the design of real-world experiments to better understand the complex and subtle ways in which entanglement evolves. @Mark Merner A beta release is an initial release meant for a sub-set of users; maybe we can accomplish milestones successfully like the establishment of angle pairs, the measuring of causal invariance. What are these companies going to do, how are these technologies going to develop.

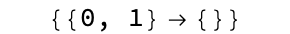
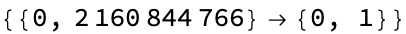
baseSteps[steps_, output_, options___] := 
  QuantumToMultiwaySystem[<|
    "Operator" -> {{1 + I, 1 - I}, {1 - I, 1 + I}}, 
    "Basis" -> {{1, 0}, {0, 1}}|>, {1 + I, 1 - I}, steps, output, 
   "IncludeStepNumber" -> True, "IncludeStateID" -> True, options];

baseSteps[2, "AllEventsList"];
baseSteps[3, "CausalGraph", "IncludeInitializationEvents" -> True]
baseSteps[3, "EvolutionCausalGraph", "IncludeEventInstances" -> True]
baseSteps[3, "StatesGraph", "IncludeStateWeights" -> True]
baseSteps[3, "AllStatesList", "IncludeStatePathWeights" -> True];
baseSteps[2, "StatesCountsList"]
baseSteps[3, "CausalGraphInstances", "MaxItems" -> 5]
baseSteps[3, "EvolutionCausalGraph", "LineThickness" -> 2]
baseSteps[3, "CausalGraph", "IncludeInitializationEvents" -> True, 
 "IncludeEventInstances" -> True]
baseSteps[2, "AllStatesList", 
 "StateRenderingFunction" -> (Style[#1, Red] &), 
 "EventRenderingFunction" -> (Style[#1, Blue] &)]
baseSteps[2, "AllStatesList", "GivePredecessors" -> True, 
 "GiveResolvents" -> True]
baseSteps[3, "CausalGraph", "IncludeSelfPairs" -> True]
baseSteps[3, "CausalGraph", "IncludeFullBranchialSpace" -> True]
baseSteps[3, "CausalGraph", "LineThickness" -> 3]

Let's look at an analogy! @Mark Merner People had had electricity for 60 years and always thought it would be possible to transmit the human voice through an electrical line and hear it on the other end, but only when Alexander Graham Bell came along in 1874 did that actually work. The herd of scientific belief went in the direction of complete nonsense and I think we see that in all sorts of places where, oh Mark, I've been deeply involved in them; the continuity of space. Space is continuous.

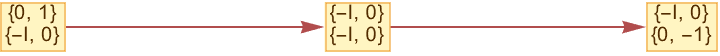
Using the QuantumToMultiwaySystem in a high-dimensional (11D) setting, we've got to specify the operators & basis, to be used. The 5 Sigma Wigner Experiment, originally conducted by the Proietti group in Europe and the Bong group in Australia, tested the intriguing concept of Wigner's friend paradox!

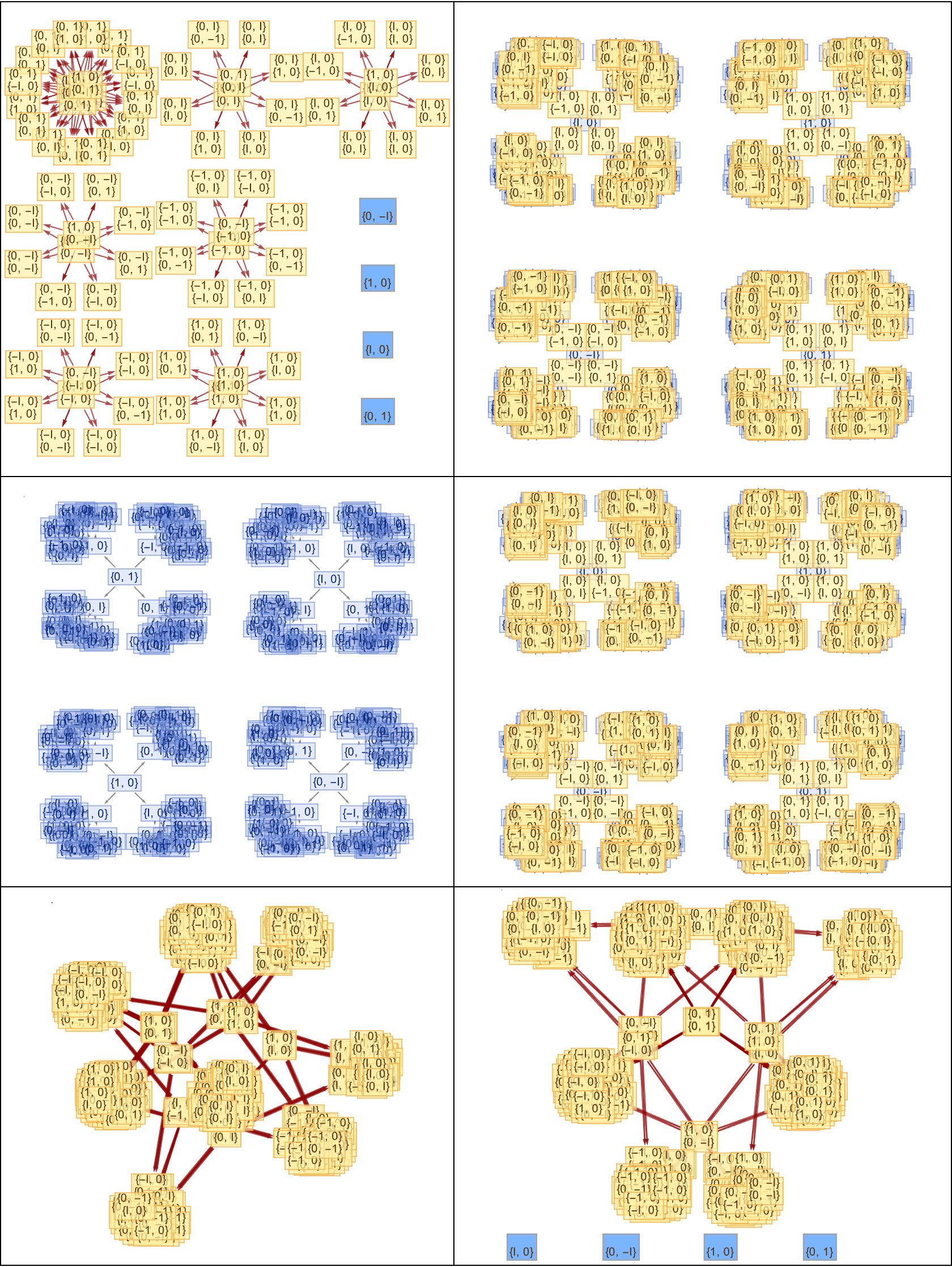
Curry-Howard-Lambek + Church-Turing-thesis..does that make all proofs physical? Yes, it's an isomorphism that has the potential; make all proofs physical, simulate and visualize quantum processes in multi-dimensional spaces. The causal graph explores the strange nature of measurement in quantum mechanics. Charm Quarks & Anti-Charm Quarks; what's in-between them?

withStepState[operator_, basis_, initState_, steps_, output_, 
   options___] := 
  QuantumToMultiwaySystem[<|"Operator" -> operator, "Basis" -> basis|>,
    initState, steps, output, "IncludeStepNumber" -> True, 
   "IncludeStateID" -> True, options];
withStepState[{{1, 1 + I}, {1 + I, 1}}, {{0, 1}, {1, 0}}, {1 + I, 
  1 - I}, 4, "EvolutionCausalGraphStructure", 
 "IncludeStateWeights" -> True]
withStepState[{{0, 1}, {1, 0}}, {{1, 0}, {0, 1}}, {1, 
  0}, 6, "EvolutionGraph"]
withStepState[{{1, 1 + I}, {1 + I, 1}}, {{0, 1}, {1, 0}}, {1 + I, 
  1 - I}, 4, "CausalGraphInstances", "MaxItems" -> 15]
quantumFunc[operator_, basis_, initState_, steps_, output_, 
   options___] := 
  Module[{processedOperator}, 
   processedOperator = ConjugateTranspose[operator . operator];
   withStepState[processedOperator, basis, initState, steps, output, 
    options]];
quantumFunc[{{1, 1 + I}, {1 + I, 1}}, {{0, 1}, {1, 0}}, {1 + I, 
  1 - I}, 4, "StatesGraphStructure", "IncludeStateWeights" -> False]

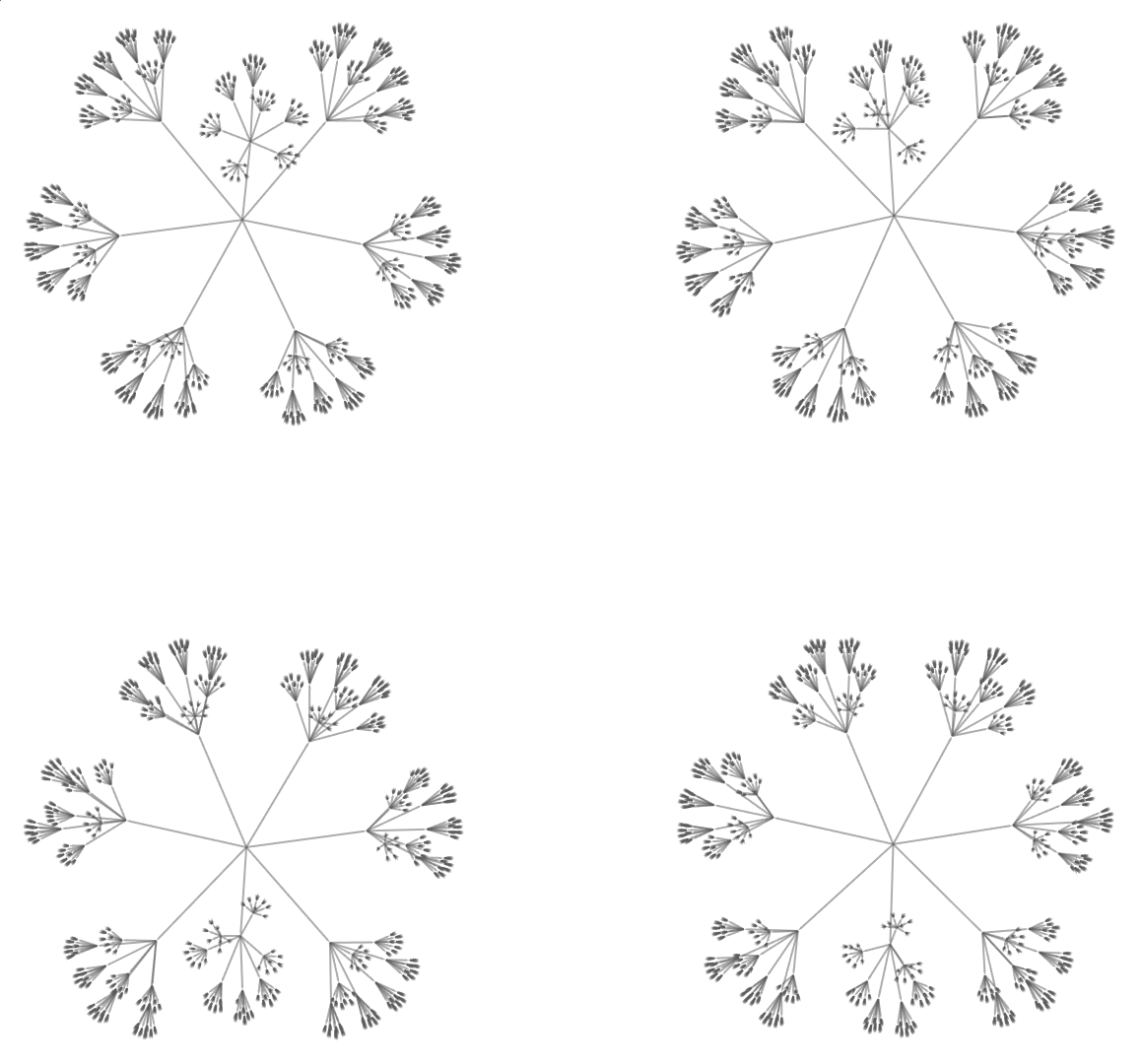
This is even stranger than the strangest nature of measurement, that is in quantum mechanics. Physical processes occurring at one location do not depend on the properties of objects at other locations; they absolutely did not know it was a star exploding. "Causal invariants", are mathematical objects that stay the same under a specific set of transformations. That is the result of the simulation that is the concept of what physical processes really go on in the six entanglement simulations. Four of them correspond to a Bell test, and two lines correspond to communications, with Wigner's friends.

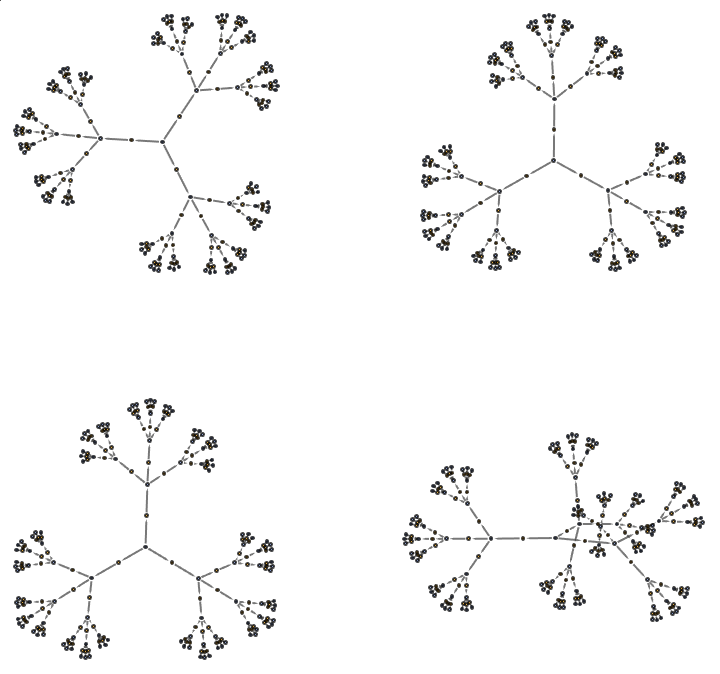
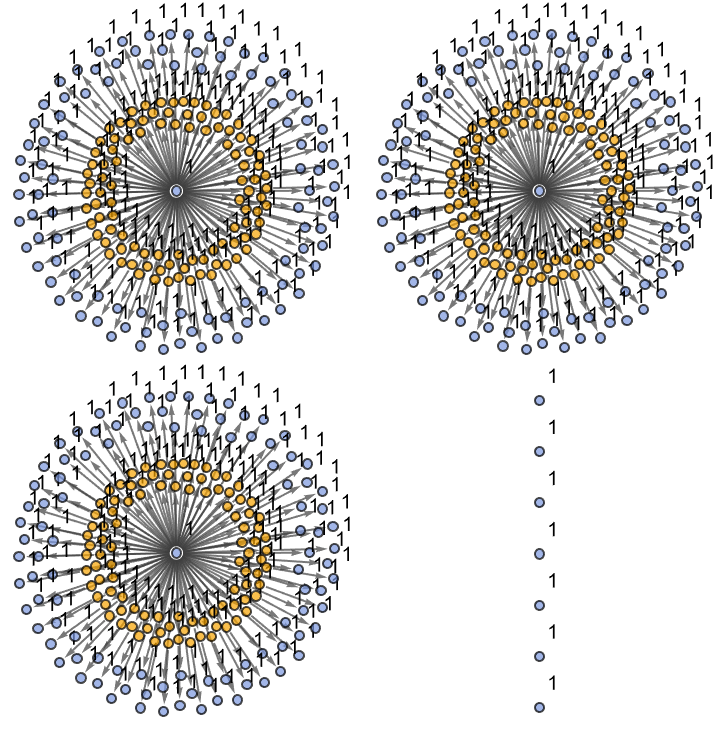
withOperatorBasis[output_, options___] := 
  QuantumToMultiwaySystem[<|"Operator" -> {{0, 1}, {1, 0}}, 
    "Basis" -> {{1, 0}, {0, 1}}|>, {0, 1}, 5, output, options];
withOperatorBasis["CausalGraph", "IncludeEventInstances" -> True]
withOperatorBasis["CausalGraph", "IncludeStepNumber" -> True, 
 "IncludeStateID" -> True]
withOperatorBasis["EvolutionEventsGraph", "IncludeStepNumber" -> True,
  "IncludeStateID" -> True]

With regard to the photons, the physical correlates of quantum multiway diagrams in nature, like when the sun got covered, and everybody freaked out they ran away from the battle..we could turn off the entanglement between Wigner and his friends. I would not be surprised that Thales and Ptolemy knew about that all along! The Antikythera, people would prove the best theorems about astronomy.

operator = {{0, 1, -Cos[2 ((2 \[Pi])/8 - (1 \[Pi])/8)], 1, 0},
   (1 + I)/Sqrt[2] {0, 1, -Cos[2 ((2 \[Pi])/8 - (0 \[Pi])/8)], 1, 0},
   {1, 0, 1, 1, 1},
   {1, 0, -Cos[2 ((0 \[Pi])/8 - (0 \[Pi])/8)], 1, 0},
   (1 + I)/Sqrt[2] {0, 1, -Cos[2 ((0 \[Pi])/8 - (1 \[Pi])/8)], 1, 
     0}};
basis = {{1, 1, 1, 1, 1},
   {0, 1, 1, 1, 1},
   {0, 0, 1, 1, 1},
   {0, 0, 0, 1, 1},
   {0, 0, 0, 0, 1}};
initState = {{1, 0, 1, 1, 1},
   {0, 1, 1, 1, 1} - {0, 0, 1, 1, 0},
   {0, 1, 1, 1, 1}};
timeFn[tRange_, output_, options___] := AbsoluteTiming[Table[
    QuantumToMultiwaySystem[<|"Operator" -> operator, 
      "Basis" -> basis|>, initState, t, output, options],
    {t, tRange}]];
timeFn[1, "EvolutionCausalGraphStructure", 
 "IncludeStateWeights" -> True, VertexLabels -> "VertexWeight"]
timeFn[1, "EvolutionCausalGraphStructure", 
 "IncludeStateWeights" -> True, VertexLabels -> "VertexWeight", 
 "IncludeStepNumber" -> True, "IncludeStateID" -> True]
QuantumToMultiwaySystem[<|"Operator" -> {{0, 1}, {1, 0}}, 
  "Basis" -> {{1, 0}, {0, 1}}|>]

Our new generation of Sigma5 level type inequality experiments, also known as the Wigner's Friends experiments, are freely accessible via the QuantumToMultiwaySystem tool. The rational unified phases, meta-linguistic awareness is the consciousness of forming languages which expresses memes transcending specific expression; in that sense we are aware of the distinct stages in the evolution and completion of quantum entanglement, with our photon polarization coincidence measurements. These approaches simulate various experiments informing the design of real-world experiments..how we understand the complex and subtle ways in which entanglement evolves. Everything is made out of water, maybe the world is made of discrete things like atoms.

data = QuantumToMultiwaySystem[<|
    "Operator" -> {{1 + I, 1 - I}, {1 - I, 1 + I}},
    "Basis" -> {{1, 0}, {0, 1}}|>,
   {1 + I, 1 - I},
   2,
   "AllStatesList",
   "IncludeStepNumber" -> True,
   "IncludeStateID" -> True,
   "StateRenderingFunction" -> Automatic,
   "EventRenderingFunction" -> Automatic,
   MaxItems -> 10];
edges = Flatten[MapIndexed[Thread[First[#2] -> Values[#1]] &, data]];
vertices = Union[Flatten[edges]];
Graph[vertices,
 edges,
 VertexLabels -> "Name",
 ImageSize -> Large,
 VertexSize -> 0.4,
 VertexLabelStyle -> Directive[RGBColor[1, 0, 1], Italic, 12]]
QuantumToMultiwaySystem[<|
  "Operator" -> {{1 + I, 1 - I}, {1 - I, 1 + I}},
  "Basis" -> {{1, 0}, {0, 1}}|>,
 {1 + I, 1 - I},
 2,
 "CausalGraph",
 "IncludeInitializationEvents" -> True,
 "IncludeEventInstances" -> True]

The Guest star, what was it? At the hands of the Catholic Church actually, yes, the stars are like the sun but far away. I suppose it's really the exploration of quantum entanglement that gets us where we need to be. When I read your article, I was so emotionally starstruck that I was unable to introduce the concept of an entanglement life cycle like you did.

data = {{0, 2}, {0, 4}, {3 Pi/8, 0}, {3 Pi/8, -2 Sqrt[2]}};
    operator1 = {{1 + I, 1 - I}, {1 - I, 1 + I}};
    operator2 = {{0, 1}, {1, 0}};
    basis = {{1, 0}, {0, 1}};
    initialState1 = {1 + I, 1 - I};

That's such a creative next phase! You could define an experiment based on the complex network graph and the QuantumToMultiwaySystem tool. I suppose it's just a matter of defining what types of interactions and transitions between states that we make, quickly, such that we can experimentally measure these things that show up on the graph like quantum phenomena, entanglement properties, specific state transitions, you know how it goes.

BarChart[
 data[[All, 2]],
 BarSpacing -> 0.3,
 ChartLabels -> Placed[data[[All, 1]], Below],
 ChartStyle -> "Pastel",
 ChartLegends -> Placed[{
    "{0, 2}",
    "{0, 4}",
     "{3 Pi/8,0}",
     "{3 Pi/8,-2 Sqrt[2]}"
    },
   Right],
 LabelingFunction -> Above,
 AxesLabel -> {"Key", "Value"},
 PlotLabel -> "Histogram of Data",
 ImageSize -> Large]

It's sort of hard to imagine that this is data in the complex plane. if only we had more access to the current technology before things get more experimental. We've got all these high-energy systems, like let's say we want to design these histograms. It's sort of like designing rockets, those hand-crafted leagues of graphs that could represent anything from a quantum state transition graph or a causal graph, from a multiway system simulation to the visualization of the evolution of quantum states which just goes to show how different quantum states are related to each other. We start out with the binary dimensionality of the data, the Law of the Excluded Middle and then we get this graph and fluff it up a bit.

ListPlot[
 Transpose[data],
 PlotMarkers -> {"\[FilledCircle]", "\[FilledSquare]"},
 PlotLegends -> Placed[{"X-value", "Y-value"}, Above],
 AxesLabel -> {"Index", "Value"},
 PlotLabel -> "List Plot of Transpose[data]",
 GridLines -> Automatic,
 Method -> "Frame" -> True,
 Background -> Transparent,
 PlotRangePadding -> 0.2,
 ImageSize -> Large,
 GridLinesStyle -> Directive[GrayLevel[0.7], Dashed],
 PlotStyle -> {Directive[Orange, PointSize[0.03]], 
   Directive[Blue, PointSize[0.03]]}
 ]

The only way I would describe it is as the concept of superposition where a particle can be in multiple states at once until it's measured. It's sort of like posting emojis and doing facial recognition, and going from something like a placeholder to emojis that can link us to different types or groups of states, something we could graph where the direction of the arrows shows the direction of state evolution or time progression...so we can go from emojis to the visualization of quantum phenomena that are not yet experimentally verifiable but for which we have the side-by-side hypotheses based on these simulations in a thousand different avenues that allow us to advance our understanding of quantum mechanics and quantum computing; 500 generations and wow, my whale is talking to me! That's why these plots exist, there's no parallel word to describe what happens in Mathematica. All the founders of these quantum experiments, they use Mathematica whereas the low-level folks they all just use low-level programming languages.

Graphics3D[{
  Sphere[{0, 0, 0}, 1],
  Text[Style["0", 12], {0, 0, 1}],
  Text[Style["1", 12], {0, 0, -1}],
  Text[Style["+", 12], {1, 0, 0}],
  Text[Style["\[Minus]", 12], {-1, 0, 0}],
  Text[Style["+i", 12], {0, 1, 0}],
  Text[Style["\[Minus]i", 12], {0, -1, 0}]},
 Boxed -> True, Lighting -> "ThreePoint", ImageSize -> 300]

Now, I don't think I was quite able to generate these plots but here's the ball representing the three-point space in which we operate. So what we're going to get is the natural shape of the ball without any data added to it, it's a real live representation of how we can simulate quantum worlds which really just means the fabric of the cosmos, all those acres of land that can allow us to illustrate extensions to our research, like you said, where we can get Sigma5 level type inequality experiments such as Wigner's Friends experiments using the QuantumToMultiwaySystem resource function, so we've got some related function in the Resource Function Repository the only question is which one is it?

data = {
   {0, 2},
   {0, 4},
   {(3 \[Pi])/8, 0},
   {(3 \[Pi])/8, -2 Sqrt[2]},
   {(2 \[Pi])/8, 1},
   {(2 \[Pi])/8, -2},
   {(4 \[Pi])/8, -1}
   };
colors = {Red, Green, Blue, Purple};
plot1 = Plot[{Sin[2 k], 2 Cos[3 k], 3 Cos[4 k], 4 Sin[2 k]},
   {k, 0, \[Pi]}, PlotStyle -> colors, Filling -> Axis,
   PlotLegends -> 
    SwatchLegend[
     colors, {"Sin[2k]", "2Cos[3k]", "3Cos[4k]", "4Sin[2k]"}],
   FillingStyle -> Directive[Opacity[0.1], colors]];
colorsWarm = {Orange, Brown, Yellow, Pink};
plot2 = Plot[{Sin[k], Cos[k], Tan[k], Cot[k]},
   {k, 0, \[Pi]}, PlotStyle -> colorsWarm, Filling -> Axis,
   PlotLegends -> 
    SwatchLegend[colorsWarm, {"Sin[k]", "Cos[k]", "Tan[k]", "Cot[k]"}],
   FillingStyle -> Directive[Opacity[0.1], colorsWarm]];
colorsCool = {Cyan, Magenta, LightBlue, DarkGreen};
plot3 = Plot[{2 (3 Cos[2 k] - Cos[3 2 k]), 4 Cos[2 k], 
    3 Cos[2 k] - Cos[3 2 k], 6 Cos[2 k]},
   {k, 0, \[Pi]}, PlotStyle -> colorsCool, Filling -> Axis,
   PlotLegends -> 
    SwatchLegend[
     colorsCool, {"2(3Cos[2k]-Cos[3*2*k])", "4Cos[2k]", 
      "3Cos[2k]-Cos[3*2*k]", "6Cos[2k]"}],
   FillingStyle -> Directive[Opacity[0.1], colorsCool]];
Show[plot1, plot2, plot3,
 ListPlot[data, PlotStyle -> Directive[PointSize[Large], Black]],
 Ticks -> {
   {0.001 \[Pi], \[Pi]/8, \[Pi]/4, 3 \[Pi]/8, \[Pi]/2, 5 \[Pi]/8, 
    6 \[Pi]/8, 7 \[Pi]/8, \[Pi]},
   {4 Sqrt[2], 2, 4, 2 Sqrt[2], -2 Sqrt[2], -4, -6}},
 PlotRange -> All, ImageSize -> Large, AxesStyle -> Thick,
 GridLines -> Automatic, GridLinesStyle -> Directive[Gray, Dashed]]

If there's one thing I really enjoyed about your post! I think it's these kinds of graphs, I don't know how many times I read your post and saw how we can describe a more general approach to explore quantum entanglement. Who is we? Well, we have this post about the four phases in the life cycle, of entanglement that are Completion, Propagation, Collapse, or Transfer. Maybe we could challenge the way that quantum mechanics is traditionally taught and put your polarization coincidence measurements between detector pairs into the limelight, the vectorization technique that it provides. And we've got all these string literals not to mention DarkGreen, that's the kind of everlasting color schemes that we might find in the function repository. It's sort of an inversion of the idea that we select everything at once and then pick out the different variables we want, reading different variable names, it's similar to learning Python in one week except when it's not. Because the changes here are more subtle. It's not just the complex patterns that suggest a lifecycle of entanglement, it's not just the collapse of the wave function. It's more like a completion with entanglement concluding in a collapse or transfer phase.

\[Alpha] = 2 \[Pi]/3;
\[Beta] = \[Pi]/4;
a = \[Pi]/8;
b = 0;
styledGrid = Grid[
  {{"Polarizer Angle Names", Style["\[Alpha]", Italic], 
    Style["\[Beta]", Italic], Style["a", Italic], Style["b", Italic], 
    ""},
   {"Polarizer Angle Values", \[Alpha], \[Beta], a, b}},
  BaseStyle -> {FontSize -> 12},
  Frame -> All,
  Background -> {None, {LightCyan, None}},
  FrameStyle -> Directive[GrayLevel[0.7], Thickness[0.003]],
  Alignment -> {Center, Center},
  ItemSize -> {{Automatic, Automatic, Automatic, Automatic, Automatic,
      2}},
  Spacings -> {2, 1},
  Dividers -> {{False, False, False, False, False, True}, {True, 
     True}}]

So what we get is this autonomous scientific endeavor to reconcile quantum mechanics with general relativity and see what these experiments cough up. I thought that the loops might symbolize things like states or conditions that recur, the theme of feedback unto ourselves, which is exactly what we need. How do we need it? I am an idiot. We can have a state lead to itself either directly or through a series of transitions. You could do something like the Force in Star Wars as a field of entanglement and bridge the gap between this phase and that next phase by exploring stuff like quantum decoherence and information storage. You should also do Schrödinger's cat and demonstrate how entangled particles exhibit a connection that transcends space. That would make things both educational and entertaining.

operator1 = {{1 + I, 1 - I}, {1 - I, 1 + I}};
basis = {{1, 0}, {0, 1}};
results = Table[
  ResourceFunction["QuantumToMultiwaySystem"][
   <|"Operator" -> operator1, "Basis" -> basis|> -> "Random",
   {1 + I, 1 - I}, t, "EvolutionCausalGraphStructure"],
  {initialConditions, initialConditionsList},
  {t, 2, 10}]

And last but not least, it's not like we have some dark mode of matter we're just building upon a common feature of complex systems wherein a quantum system can evolve in multiple ways and lead to different possible outcomes and that's how we get the direction of time progression or state evolution...whether it's photons, atoms, or electrons..and we need some quantum optics equipment, detectors..it's like the mathematical walkthrough of how to tell the story of the state transitions and outcomes that take place by nature which really just means that it depends on how you define your experimental design. I was drawn in by the extraordinary interactions described in the present experimental setup, like the method for initiating state transitions and measuring outcomes as they interact with the theoretical predictions that we make.