Queen[board_, walk_] :=
Graph[board,
UndirectedEdge @@@
Select[Subsets[board, {2}],
AnyTrue[walk,
Function[{step}, (step[[1]] != 0 && #[[1, 2]] == #[[2, 2]] &&
Mod[Abs[#[[1, 1]] - #[[2, 1]]], step[[1]]] ==
0) || (step[[2]] != 0 && #[[1, 1]] == #[[2, 1]] &&
Mod[Abs[#[[1, 2]] - #[[2, 2]]], step[[2]]] == 0)]] &],
VertexLabels -> "Name"]; vertices =
Round /@
GraphEmbedding[GridGraph[{1, 38}]]; steps = {{1, 0}, {0,
1}}; Queen[vertices, steps]
Hi @Cael Harris I never thought we would coordinate like this but this project is dynamite, what is the generalized version of chessboard lattices that allow the "Queen" (Walker) to move in any type of direction with its range led by the core lattice structure? It's just like Mandelbrot said. Also, I never thought I would see the stochastic evolution of random self-avoiding walks on these graphs, I found your project fun and energetic, graphic and visual.

Check out this graph!
Column[Apply[
Sequence, {GridGraph[#],
Queen[Round /@
GraphEmbedding[GridGraph[#]], {{1, 0}, {0, 1}}]} & /@ {{1,
2}, {2, 3}, {3, 4}, {5, 16}}, {1}]]
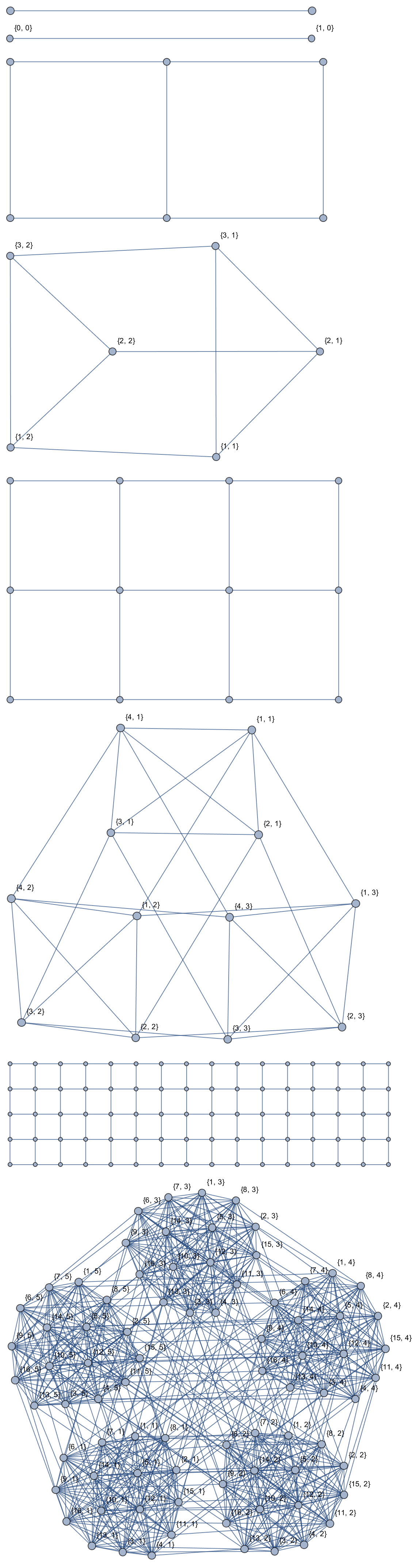
What do you do when the Queen is not allowed to revisit a vertex?
Manipulate[
With[{board =
GraphEmbedding[
GridGraph[
Dimensions[
ResourceFunction[
"WolframModel"][{{1, 1, 2}, {3, 2, 4}} -> {{2, 2, 4}, {5, 2,
3}, {3, 5, 1}}, {{0, 0, 0}, {0, 0, 0}}, n,
"FinalState"]]]], walk = {{0, 1}, {1, 0}}},
Graph[Queen[board, walk], VertexLabels -> "Name",
VertexLabelStyle -> Directive[RGBColor[0, 0.5, 0], Bold, 12],
VertexStyle -> RGBColor[0.8, 0.1, 0.2], VertexSize -> 0.1,
EdgeStyle -> Directive[RGBColor[0.5, 0.5, 0.7], Dashed]]], {n, 1,
14, 1, Appearance -> "Open"}]
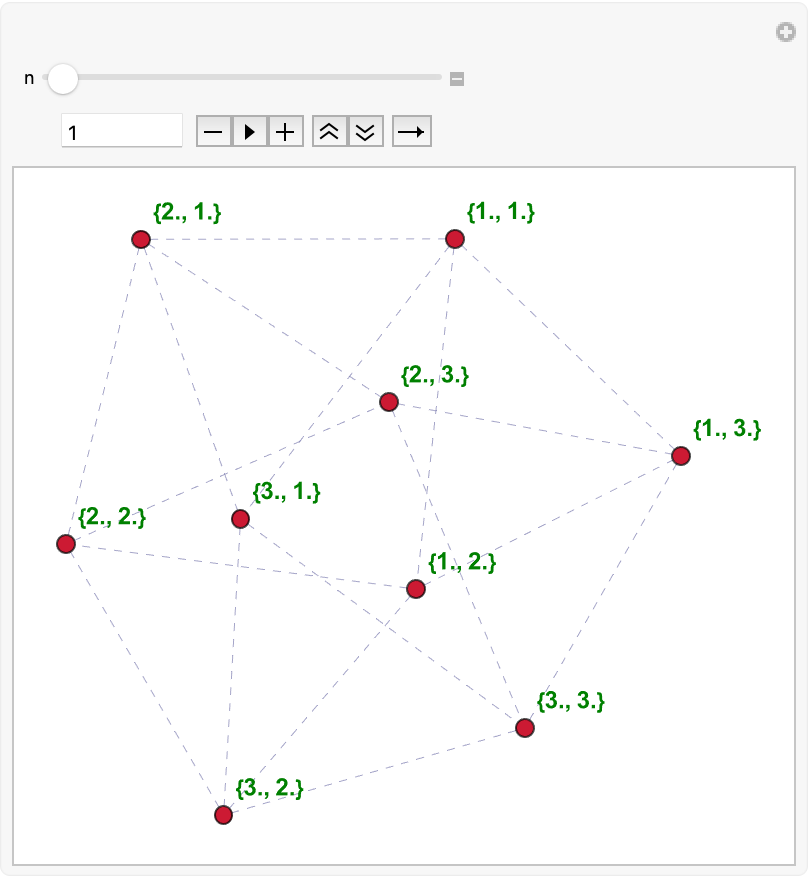
@Cael Harris I think I finally understand that the walks are multi-way systems, and that the game of Trike is a part of the partitioning process.
board = Round /@ GraphEmbedding[GridGraph[{3, 3}]];
walk = {{1, 1}, {0, 0}};
HighlightGraph[Queen[board, walk], {1, 1},
GraphHighlightStyle -> "Thick",
VertexLabelStyle -> Directive[RGBColor[0, 0.5, 0], Bold, 12]]
You can train on the stochastic evolution of random self-avoiding walks on these graphs..you know how every day there are gobs of video that have been running..maybe a security camera? That doesn't have actual data, the data doesn't exist. But it's possible to train from the videos directly. Do you think that the Trike algorithm can be optimized via multi-way, diverse winning conditions?
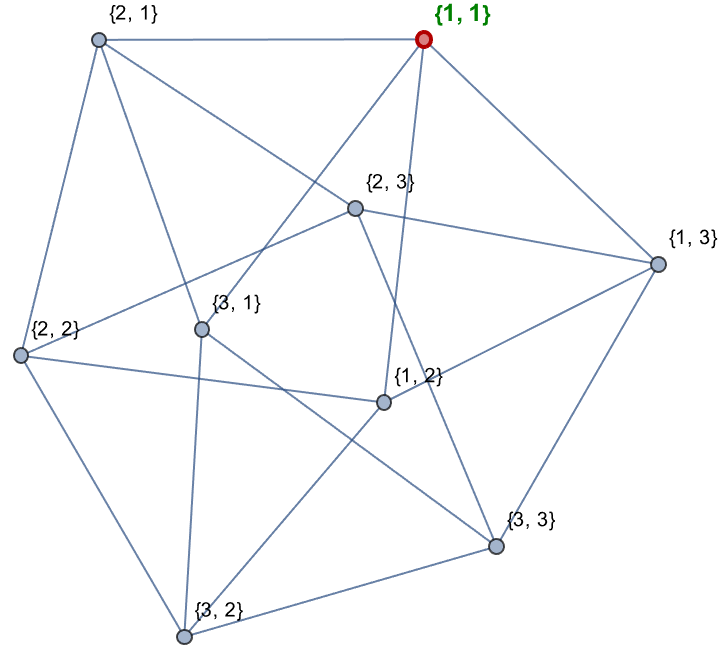
With their partitioned edges and self-avoiding vertices, I know these graphs might seem a little watery; meanwhile we've got some research direction in doing the Trike algorithm, maybe we want some full-fledged optimization of play according to winning conditions. For better or worse this project has a lot of potential from the multi-way structure there's a lot of things it's good for. @Cael Harris
With[{board = Round /@ GraphEmbedding[GridGraph[{1, 200}]],
walk = {{0, 1}, {1, 0}}},
HighlightGraph[Queen[board, walk],
PathGraph[(Function[{graph, start},
Module[{visited = {}, stack = {start}},
While[stack =!= {},
With[{current = Last[stack]},
If[! MemberQ[visited, current], AppendTo[visited, current];
stack = Join[stack,
Complement[AdjacencyList[graph, current], visited]],
stack = Most[stack]]]]; visited]][Queen[board, walk],
First[VertexList[Queen[board, walk]]]])],
GraphHighlightStyle -> "Thick", VertexSize -> 0.1,
VertexLabels -> "Name",
VertexLabelStyle -> Directive[RGBColor[0, 0.5, 0], Bold, 12]]]
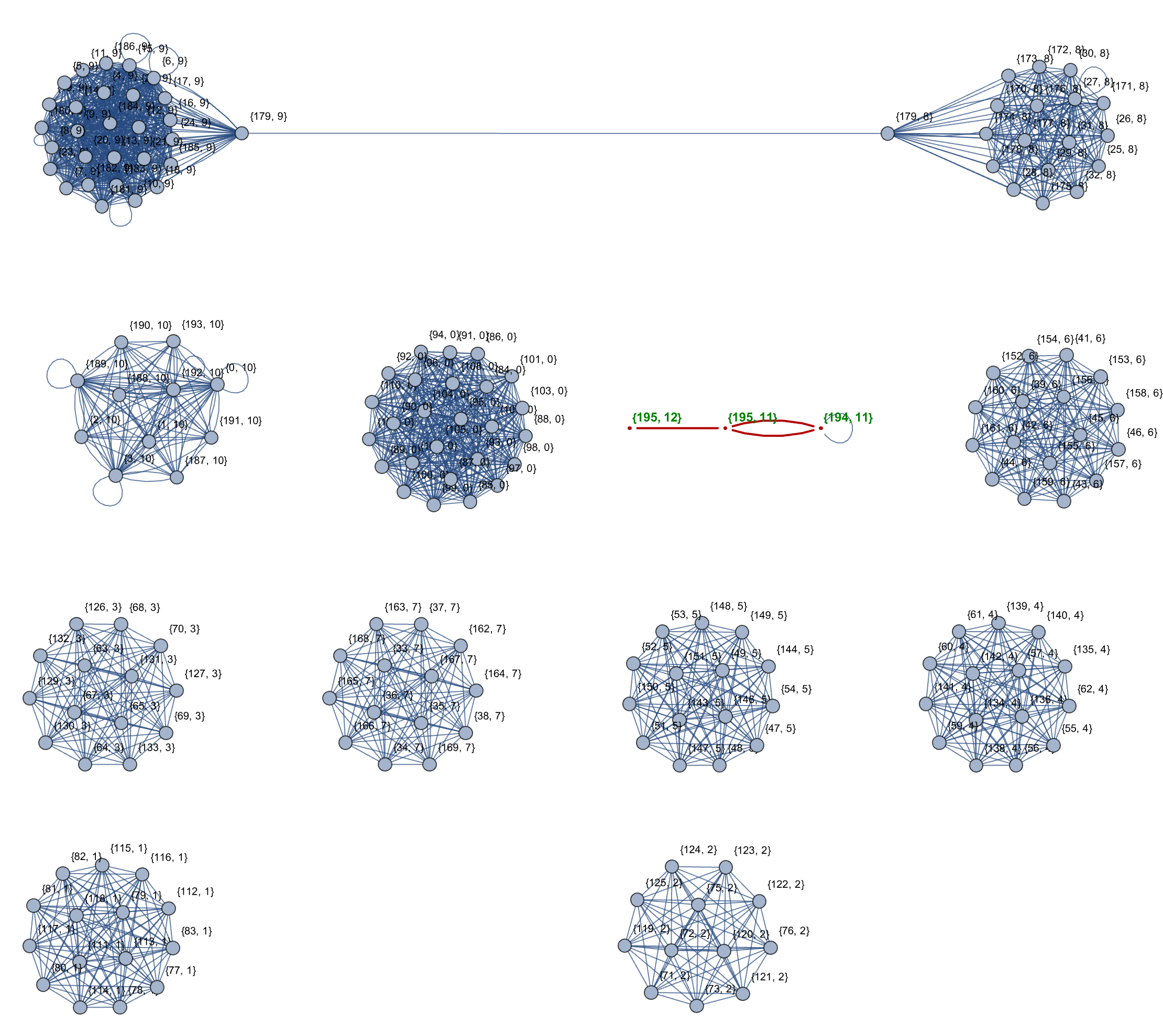
At what point can we expose and track these things, like the Queen walks: generalize graphs based on the movement of the Queen chess piece on a lattice?