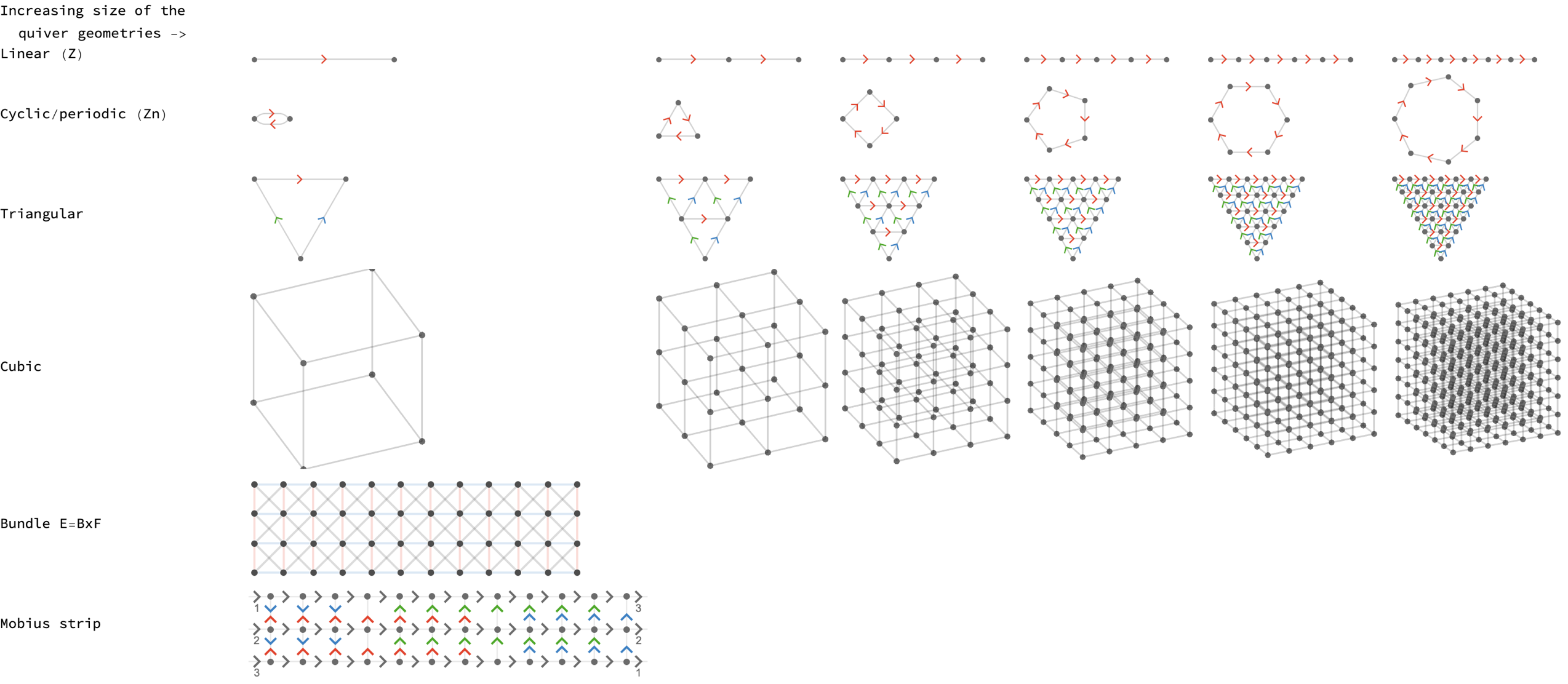
@Sinuhe Perea , the tutorial that you have produced is all using simple discrete lattice geometries. Those topological invariants that make the pseudo-particles, the skyrmions...the mobius strip.

sizes = Range[2, 7];
Grid[{
  {"Increasing size of the quiver geometries ->"},
  {"Linear (Z)", 
   Sequence @@ Table[LineQuiver[n, ImageSize -> 130], {n, sizes}]},
  {"Cyclic/periodic (Zn)", 
   Sequence @@ Table[CycleQuiver[n], {n, sizes}]},
  {"Triangular", 
   Sequence @@ 
    Table[TriangularQuiver[n, ImageSize -> 85], {n, sizes}]},
  {"Cubic", 
   Sequence @@ Table[CubicQuiver[n, ImageSize -> 150], {n, sizes}]},
  {"Bundle E=BxF", TrivialBundleGraph[12, 4, ImageSize -> 300]},
  {"Mobius strip", MobiusStrip[12]}},
 Alignment -> Left
 ]

Manipulate[{Length[
   FindAllBundleSections[QuiverBundleGraph[bss, fbr]]], fbr^bss, 
  N[Length[FindAllBundleSections[QuiverBundleGraph[bss, fbr]]]/
    fbr^bss, 4]}, 
 Style["Possible/Total States, Ratio" Dynamic[bss] Dynamic[fbr], 10, 
  Bold], {{bss, 4, "n=Base size"}, 3, 10, 1, 
  ImageSize -> Tiny}, {{fbr, 3, "m=Fibre size"}, 2, 10, 1, 
  ImageSize -> Tiny}]

MatrixForm[
 Table[N[Length[FindAllBundleSections[QuiverBundleGraph[i, j]]]/
    j^i], {i, 2, 7}, {j, 2, 7}]]

@Sinuhe Perea QuiverBundleGraph produces such massive quantities that you could be an Ambassador of Wolfram. It's like how Spongebob broke the laws of physics.

QuiverBundleGraph, corresponds to the poetic interpretation of @Jonathan Gorard we saw his lambda calculus in C++, it was so good to see how even primes are odd.

Manipulate[Module[{hh, sky}, hh = \[Pi]/2*hel;
  sky = Flatten[
    Table[
     {
      {st Cos[\[Theta]] - Cos[\[Theta] + hh] Sin[-\[Pi] st]/20,
       st Sin[\[Theta]] - Sin[\[Theta] + hh] Sin[-\[Pi] st]/20,
       -Cos[-\[Pi] st]/20},
      {st Cos[\[Theta]] + Cos[\[Theta] + hh] Sin[-\[Pi] st]/20,
       st Sin[\[Theta]] + Sin[\[Theta] + hh] Sin[-\[Pi] st]/20,
       +Cos[-\[Pi] st]/20}
      },
     {st, 0, 1, 0.05},
     {\[Theta], 0, 2 \[Pi], 0.1}
     ], 1];
  Show[
   {
    Graphics3D[{
        RGBColor[1, 0.19, 0.59, 1],
        Arrowheads[0.01],
        Arrow[Tube[#, 0.001]
         ]} & /@ sky]
    },
   ImageSize -> 500,
   Boxed -> False]
  ], Style["Domain wall transformation to skyrmion", 12, Bold],
 {{hel, 0.01, "Character, 0=Neel, 1=Bloch"},
  0, 1, 0.01, ControlPlacement -> Top}
 ]

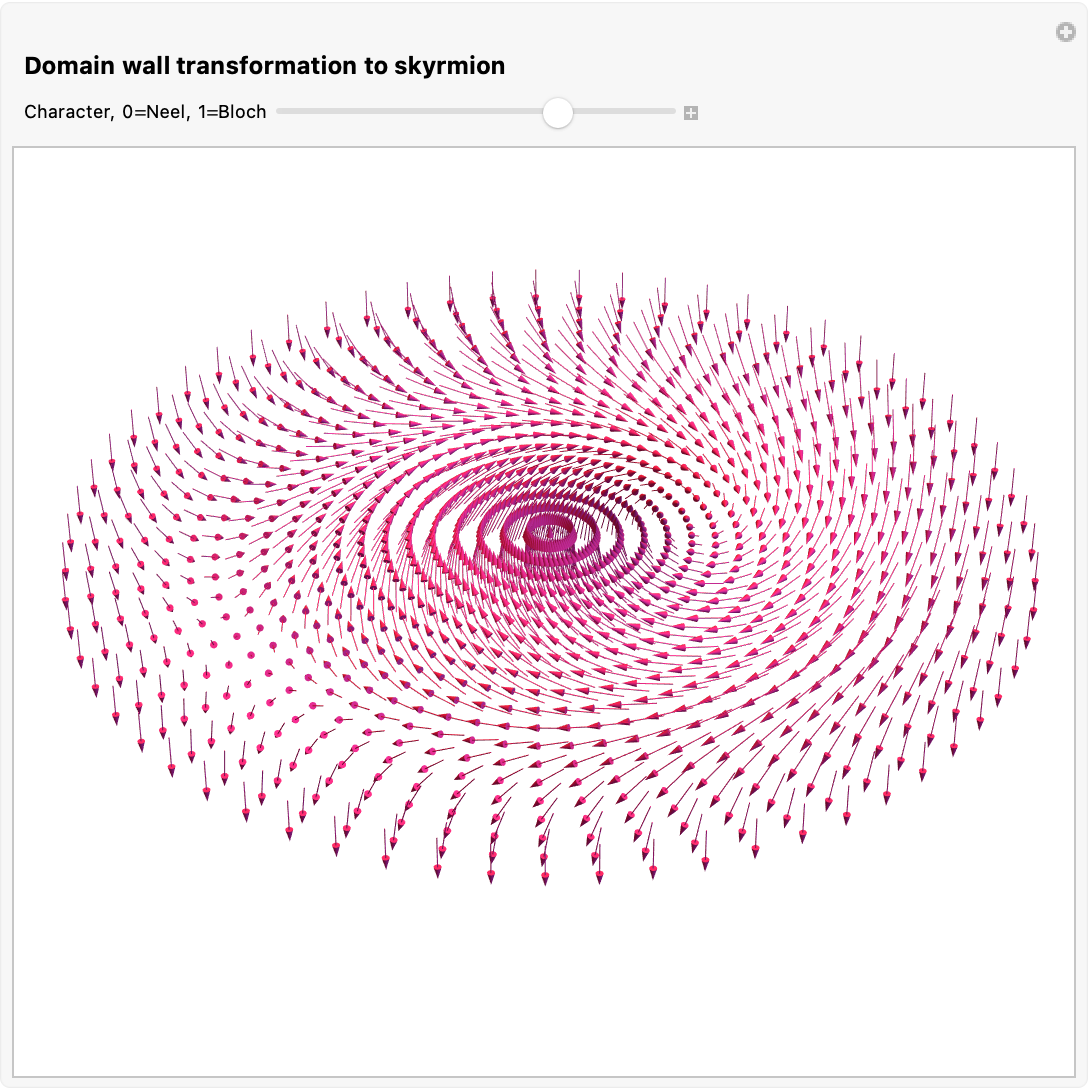
It's this physical-inspired system, the domain walls @Sinuhe Perea how is it elastic? There's a focus on quantum processes and not states. And looking back at the isomorphisms in the Ruliad they are smooth and continuous lovely treatment that you have produced, @Sinuhe Perea .