When you take a closer look at it you see the rate of entanglement as a speed limit for information propagation through branchial space, and the evolution of a system of qubits under different quantum circuits and the use of quantum gates in transforming quantum states.
oneQubitFSVelocities = Flatten[Table[
GraphVelocityFS[oneQubitStateGraph, oneQubitStrings[[i]],
oneQubitStrings[[j]]],
{i, Length[oneQubitStrings]}, {j, Length[oneQubitStrings]}], 1];
twoQubitFSVelocities = Flatten[Table[
GraphVelocityFS[twoQubitStateGraph, twoQubitStrings[[i]],
twoQubitStrings[[j]]],
{i, Length[twoQubitStrings]}, {j, Length[twoQubitStrings]}], 1];
threeQubitFSVelocities = Flatten[Table[
GraphVelocityFS[threeQubitStateGraph, threeQubitStrings[[i]],
threeQubitStrings[[j]]],
{i, Length[threeQubitStrings]}, {j, Length[threeQubitStrings]}],
1];
ListPlot[{Sort[N@DeleteDuplicates[oneQubitFSVelocities]],
Sort[N@DeleteDuplicates[twoQubitFSVelocities]],
Sort[N@DeleteDuplicates[threeQubitFSVelocities]]},
PlotStyle -> {Blue, Red, Orange},
PlotRange -> All,
PlotLabels -> {"1-Qubit Stabilizer Graph Velocities",
"2-Qubit Stabilizer Graph Velocities",
"3-Qubit Stabilizer Graph Velocities"},
PlotLegends -> Placed[Automatic, {0.8, 0.7}],
ImageSize -> 600]
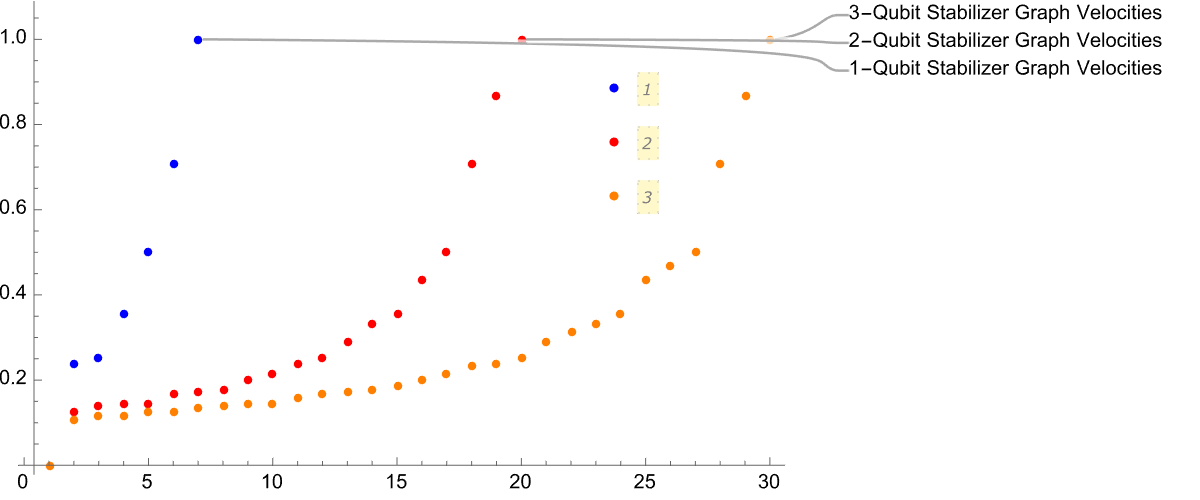
Does this look like a logarithmic scale? We can experience very intense sound in terms of decibels, but it's logarithmic. And humans may not even hear it.
ResourceFunction["MultiwaySystem"][threeQubitRules,
threeQubitStrings[[160]], 3, "EvolutionEventsGraphStructure"]
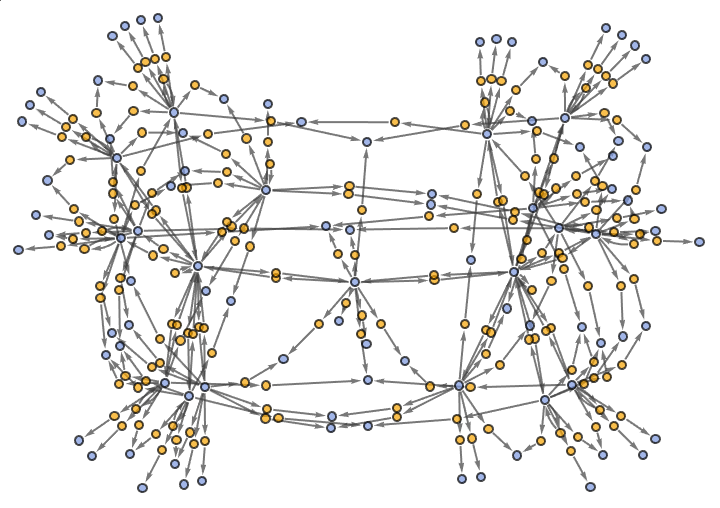
The possibilities of evolution, and actually of synthetic biological drugs are equally intriguing. We can create molecular-scale objects with computational operations and run machine learning algorithms within them to determine if they're cancer cells, among other things.
reducedThreeQubitGates = {HadamardGate[3, 2], CNOTGate[3, {1, 2}],
CNOTGate[3, 2, Pi/4], CNOTGate[3, {2, 3}]};
EntropyHighlight[
ResourceFunction["MultiwaySystem"][
ReplacementRulesBuilder[threeQubitStrings, reducedThreeQubitGates,
1], threeQubitStrings, 2, "StatesGraphStructure"]]
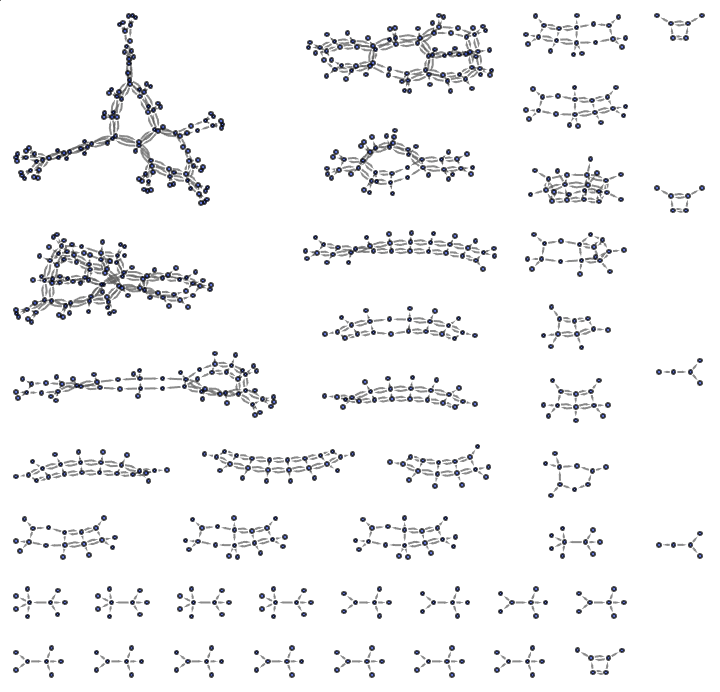
These drugs can be designed to have medical effects like puzzle pieces made to order, and we can use 3D printers to produce them.
k = 6;
n = 2^k;
edges = Table[
UndirectedEdge[i, Mod[i + 2^j, n, 1]],
{i, 0, n - 1},
{j, 0, k - 1}];
g = Graph[
Flatten[edges],
ImageSize -> Large,
GraphLayout -> {"SpringElectricalEmbedding",
"EdgeLengths" -> 0.1,
"EdgeWeighted" -> False},
EdgeStyle -> Directive[Opacity[0.5],
Hue[RandomReal[]]],
VertexStyle -> White,
VertexSize -> Medium
];
GraphPlot3D[
HighlightGraph[g,
Subgraph[g, Range[1, 2^k - 1]],
GraphHighlightStyle -> "Thick",
ImageSize -> Large]
]

My favorite thing about this article is how we can handle the Clifford group and its special properties, as well as the construction of a graph-theoretic representation of all states and operations known as a reachability graph. It's similar to the gene manipulation in E. Coli bacteria, the process is akin to exploring deep caverns inside the planet.
LayeredGraphPlot[
EntropyHighlight[twoQubitVacuumEvolutionStateGraph],
GraphLayout -> "LayeredDigraphEmbedding",
VertexShapeFunction -> "Rectangle",
EdgeShapeFunction -> "Arrow",
VertexSize -> Medium,
EdgeStyle -> Directive[Arrowheads[0.03], Black],
ImageSize -> Large
]

However, this environment is similar to Earth's, with a star of a certain size and self-assembling molecules in its capillaries. With AI-powered biological tools, we can selectively attach to specific molecules and achieve remarkable results.
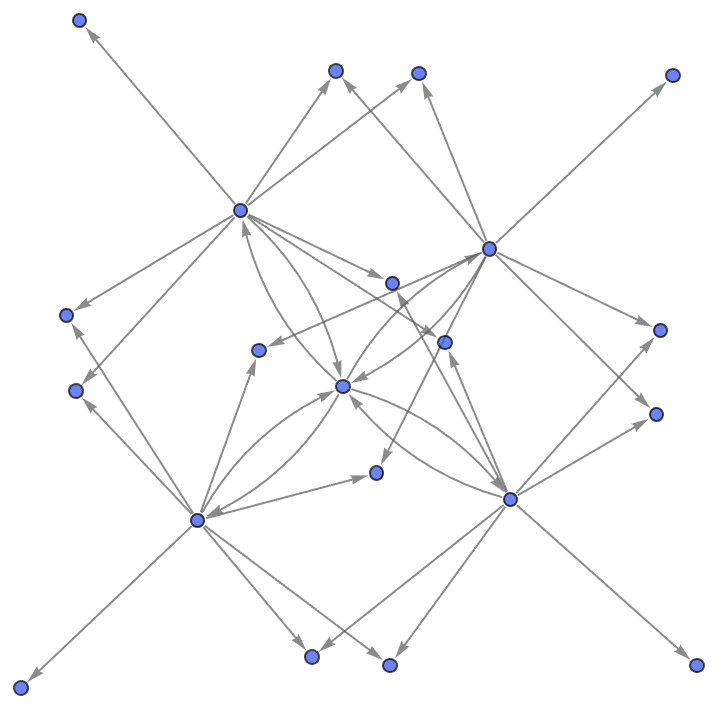
twoQubitVacuumEvolutionStateGraph =
ResourceFunction["MultiwaySystem"][twoQubitRules,
twoQubitStrings[[1]], 4, "CausalGraphStructure"];
EntropyHighlight[Graph3D@twoQubitVacuumEvolutionStateGraph]

The notion of an entropy vector is also introduced as a way to describe the entanglement structure of a particular quantum state, in simple fashion. Despite the complexity of tubes, assemblies, and machinery involved, rockets generally operate smoothly.
numQubits = 4;
numSteps = 3;
initialState =
ReplacePart[ConstantArray[{0}, 2^numQubits], 1 -> {1}];
gates = CliffordGenerators[numQubits];
states = SelectiveStateGenerator[initialState, gates, numSteps];
strings = Table[QuantumToString[states[[i]]], {i, Length[states]}];
rules = ReplacementRulesBuilder[strings, gates, 1];
stateGraph =
ResourceFunction["MultiwaySystem"][rules, strings, 1,
"StatesGraphStructure"];
EntropyHighlight[stateGraph]
However, statistics show that approximately one in fifty rockets explode, highlighting the need to improve their safety. But is this really true? There's no fundamental reason why we cannot achieve this. Take, for instance, jellyfish that emit light in the dark; their glowing property was once considered a mystery, but we now know how to replicate it.
threeQubitVacuum = ReplacePart[ConstantArray[{0}, 2^3], 1 -> {1}];
threeQubitGates = CliffordGenerators[3];
threeQubitStates =
SelectiveStateGenerator[threeQubitVacuum, threeQubitGates, 100];
threeQubitStrings =
Table[QuantumToString[threeQubitStates[[i]]], {i,
Length[threeQubitStates]}];
threeQubitRules =
ReplacementRulesBuilder[threeQubitStrings, threeQubitGates, 1];
threeQubitStateGraph =
ResourceFunction["MultiwaySystem"][threeQubitRules,
threeQubitStrings, 1, "StatesGraphStructure"];
EntropyHighlight[threeQubitStateGraph]

The rate of these quantum circuits, the representation of quantum states as vectors and their manipulation using quantum gates, such as Hadamard and CNOT gates..when I saw this I was overjoyed.