Special thanks again to @Keying Huang and @Bradley Klee for the foundational concepts, helping evolve the original maze exploration framework into an interactive game experience. This game flow mechanism isn't like anything we have had before; it allows players to quickly retry challenges and or enjoy multiple maze configurations. We could add an interactive starting screen that rejuvenates a transition into gameplay, setting initial player positions and resetting scores, and regenerating the maze configuration on each game restart. What we get is something quite like the shape of a PEZ Dispenser; players toggle the help overlay using the "H" key, keeping gameplay unobtrusive yet informative. We can't quite say it's informative yet but we can say that every time we start the regeneration of the maze configuration starts on each game restart; a centralized game state system, it concludes with real-time updates on score, number of coins left, and active enemies. Of course you could call them ghosts, you could call them blue devils with horns, or you could even render them in the shape of pots which minimizes their Euclidean distance unnecessarily creating a compelling "chase" dynamic, an efficient heuristic that is currently in the process of actively tracking and pursuing the player instead of moving randomly. Each enemy recalculates its route to get closer to the player after each player move:
mazeArray =
ReplaceAll[
ResourceFunction["RandomSierpinskiMaze"][1][[1, 1]], {5 -> 0,
0 -> 1, 4 -> 0}];
mazeDims = Dimensions[mazeArray];
startPos = {1, 1};
endPos = {mazeDims[[1]], mazeDims[[2]]};
mazeArray[[startPos[[1]], startPos[[2]]]] = 0;
mazeArray[[endPos[[1]], endPos[[2]]]] = 0;
openCells = Position[mazeArray, 0, {2}];
coins = RandomSample[Complement[openCells, {startPos, endPos}], 100];
enemyCount = 30;
enemyPositions =
RandomSample[Complement[openCells, {startPos, endPos}, coins],
enemyCount];
drawPacman[pos_] := {Yellow,
Disk[Reverse@pos - 0.5, 0.3, {20 Degree, 340 Degree}], Black,
Disk[Reverse@pos - 0.5 + {0.1, 0.1}, 0.05], Red,
Polygon[{Reverse@pos - 0.5 + {0, -0.15},
Reverse@pos - 0.5 + {0.15, -0.3},
Reverse@pos - 0.5 + {-0.15, -0.3}}]};
LightGoldenrod = RGBColor[0.933, 0.867, 0.514];
drawFuzzball[pos_] :=
Module[{base, fuzz},
base = {LightGoldenrod, Disk[Reverse@pos - 0.5, 0.2]};
fuzz = {Brown,
Table[Disk[
Reverse@pos - 0.5 + {Cos[\[Theta]]*0.25, Sin[\[Theta]]*0.25},
0.05], {\[Theta], 0, 2 Pi - Pi/4, Pi/4}]};
{base, fuzz}];
BluePotColor = RGBColor[.1, .2, .5];
PotRimColor = RGBColor[1, 0, 1];
drawBluePot[pos_] :=
Module[{potBody, potRim},
potBody = {BluePotColor, Disk[Reverse@pos - 0.05, 0.3]};
potRim = {PotRimColor, Thickness[0.005],
Circle[Reverse@pos - 0.2, 0.2]};
{potBody, potRim}];
DynamicModule[{playerPos = startPos, collectedCoins = {},
enemies = enemyPositions, gameOver = False, score = 0,
showHelpFlag = True, gameStatus = "Playing"},
Column[{Dynamic@
Grid[{{Style[ToUpperCase@gameStatus, 24, Red],
Style["Score: " <> ToString@score, 12],
Style["Coins Left: " <>
ToString[Length[coins] - Length[collectedCoins]], 12],
Style["Enemies Active: " <> ToString[Length[enemies]], 12],
Button["Play Again", (playerPos = startPos;
collectedCoins = {};
enemies = enemyPositions;
gameOver = False;
score = 0;
showHelpFlag = True;
gameStatus = "Playing";), BaseStyle -> {FontSize -> 7}]}}],
Pane[EventHandler[
Dynamic[If[gameOver,
ArrayPlot[mazeArray,
ColorRules -> {0 -> GrayLevel[0], 1 -> GrayLevel[1]},
Mesh -> True, MeshStyle -> Blue,
Epilog -> {drawPacman[playerPos],
Text[Style[
If[playerPos === endPos, "YOU WIN!", "GAME OVER!"], Red,
24], {mazeDims[[2]]/2, mazeDims[[1]]/2}],
Text[Style["Score: " <> ToString@score, Blue,
16], {mazeDims[[2]]/2, mazeDims[[1]]/2 - 2}],
Text[Style["Press R to restart", Blue,
14], {mazeDims[[2]]/2, mazeDims[[1]]/2 - 3}],
If[showHelpFlag,
Text[Style[
"Arrow keys to move\nCollect yellow coins\nAvoid purple \
enemies\nReach green exit\nPress H to toggle help", 12], {2,
mazeDims[[1]] - 1}, {-1, 1}], Nothing]},
ImageSize -> 600
],
ArrayPlot[mazeArray,
ColorRules -> {0 -> GrayLevel[0], 1 -> GrayLevel[1]},
Mesh -> True, MeshStyle -> Blue,
Epilog -> {drawPacman[playerPos],
Join @@ (drawFuzzball /@ Complement[coins, collectedCoins]),
Join @@ (drawBluePot /@ enemies),
If[playerPos ===
endPos, {Text[
Style["YOU WIN!", Green, 24], {mazeDims[[2]]/2,
mazeDims[[1]]/2}]}, {Text[
Style["Score: " <> ToString@score, Blue,
16], {mazeDims[[2]]/2, mazeDims[[1]]/2 - 2}]}],
If[! gameOver && showHelpFlag,
Text[Style[
"Arrow keys to move \[FilledUpTriangle]\
\[FilledDownTriangle]\[FilledLeftTriangle]\[FilledRightTriangle]\n\
Collect yellow coins\nAvoid purple enemies\nReach green exit\nPress H \
to toggle help", 12, Orange], {2, mazeDims[[1]] - 1}, {-1, 1}],
Nothing]}, ImageSize -> 600
]
]
], {"DownArrowKeyDown" :>
If[! gameOver && validMove[playerPos + {-1, 0}],
playerPos += {-1, 0};
If[showHelpFlag, showHelpFlag = False];
checkCoin[];
moveEnemies[];
checkEndGame[];
],
"UpArrowKeyDown" :>
If[! gameOver && validMove[playerPos + {1, 0}],
playerPos += {1, 0};
If[showHelpFlag, showHelpFlag = False];
checkCoin[];
moveEnemies[];
checkEndGame[];
],
"LeftArrowKeyDown" :>
If[! gameOver && validMove[playerPos + {0, -1}],
playerPos += {0, -1};
If[showHelpFlag, showHelpFlag = False];
checkCoin[];
moveEnemies[];
checkEndGame[];
],
"RightArrowKeyDown" :>
If[! gameOver && validMove[playerPos + {0, 1}],
playerPos += {0, 1};
If[showHelpFlag, showHelpFlag = False];
checkCoin[];
moveEnemies[];
checkEndGame[];
],
"KeyDown" :> (Module[{k =
ToUpperCase[CurrentValue["EventKey"]]},
If[k === "H", showHelpFlag = Not[showHelpFlag]];
If[gameOver && k === "R", playerPos = startPos;
collectedCoins = {};
enemies = enemyPositions;
gameOver = False;
score = 0;
showHelpFlag = True;
gameStatus = "Playing";]])
}, PassEventsDown -> False
], ImageSize -> 650
]
}], Initialization :> (validMove[pos_] :=
Module[{i, j, iConv}, {i, j} = pos;
iConv = mazeDims[[1]] - i + 1;
If[iConv < 1 || iConv > mazeDims[[1]] || j < 1 ||
j > mazeDims[[2]], False, mazeArray[[iConv, j]] === 0]];
checkCoin[] :=
Module[{coinCollected = False},
If[MemberQ[coins, playerPos] && !
MemberQ[collectedCoins, playerPos],
AppendTo[collectedCoins, playerPos];
score += 10;
coinCollected = True;]];
moveEnemies[] :=
Module[{possibleMoves, validMoves, bestMove},
enemies = Table[({ex, ey} = enemy;
possibleMoves = {{ex + 1, ey}, {ex - 1, ey}, {ex,
ey + 1}, {ex, ey - 1}};
validMoves = Select[possibleMoves, validMove];
If[validMoves === {}, enemy,
bestMove =
First[SortBy[validMoves, Norm[# - playerPos] &]];
bestMove]), {enemy, enemies}];];
checkEndGame[] := (If[
playerPos === endPos, (gameOver = True;
gameStatus = "YOU WIN!")];
If[MemberQ[enemies, playerPos], (gameOver = True;
gameStatus = "GAME OVER!")];);)
]

When you control the pawn in the maze, to reach the exit, that is fantastic @Keying Huang you could do that with character codes! Reading about your bug in the algorithm, I felt algorithmic. I was so elated to see and so when I was in the maze I saw all those shimmering lines of sight @Keying Huang you were talking about, when the knights can only see the pawn when they enter its line of sight. I had a lot of fun. Now, coins placed strategically throughout the maze can be collected, but we could also reversibly increase the player's score. Which means that the code snippet, we would have to be "sure" that the coins appear in open cells, away from the starting positions and maze walls. However, the coins (silver or gold) we render as interactive "Fuzzballs" and they know, without us even telling them where the visual experience is; it's a "delight" that effectively generates a "fog-of-war", keeping the player alert and, encouraging thorough maze exploration. Exploring this maze is like, the immediate surroundings are clearly visible, while distant or unexplored areas remain partially opaque. As the player navigates through the maze, nearby areas correspondingly become clearer although they could become more opaque depending on whether or not we simulate realistic exploration.
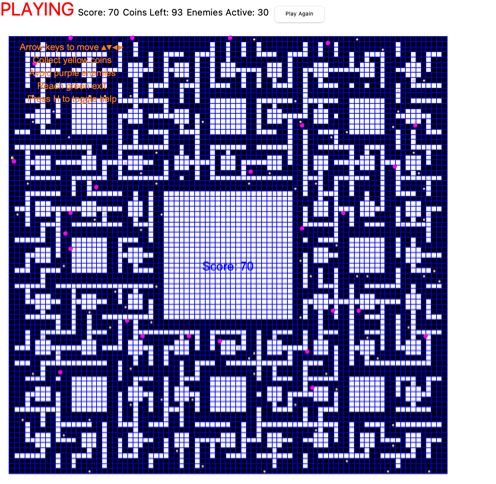
It's a little bit far-fetched but there's a bit of a skip, in the sense of how the player "represents" a "Pacman" styled character so that the "game state management" system can "allow" the player to pass through the pots, such that the advanced AI that these enemies use, generates realistic "video"; does it internally "know" physics? Possibly--but like human brains, it's likely embedded in patterns rather than explicit, narrative models we can easily interpret. Ultimately, these mazes we will operate at an anatomical, molecular scale--similar to biology. Biology already masters sophisticated molecular computations; the question is whether we'll engineer it from scratch or piggyback on evolution's achievements. Each enemy (I thought they were pots) recalculates its route to get closer to the player after each player move. Future improvements might involve further optimization of enemy pathfinding algorithms to add new layers of interaction.
DynamicModule[{gameState = "Start", playerPos, timeLeft, score,
MazeArray1, AdjGraph1, MazeD1, vList1, visitedMatrix, vertex,
updateVisibility},
Dynamic[Switch[gameState, "Start",
Column[{Style["MAZE RUNNER", 18, Bold, Red],
Style["Arrow Keys to Move", 12],
Style["Collect Coins, Avoid Enemies", 12],
Button["Start Game", (gameState = "playing";
playerPos = {2, 2};
score = 0;
MazeArray1 =
ReplaceAll[
ResourceFunction["RandomSierpinskiMaze"][4][[1, 1]], {5 -> 0,
0 -> 1}];
AdjGraph1 =
NearestNeighborGraph[Position[MazeArray1, 0], {All, 1}];
MazeD1 = Dimensions[MazeArray1];
vList1 = VertexList[AdjGraph1];
visitedMatrix = ConstantArray[False, MazeD1];
updateVisibility[pos_] := Module[{x, y}, {x, y} = pos;
Do[If[1 <= x + dx <= MazeD1[[1]] &&
1 <= y + dy <= MazeD1[[2]],
visitedMatrix[[x + dx, y + dy]] = True], {dx, -1,
1}, {dy, -1, 1}];];
vertex = vList1[[1]];), ImageSize -> 200]},
Alignment -> Center], "playing",
DynamicModule[{localVertex = vertex},
EventHandler[
Dynamic[If[localVertex == vList1[[-1]],
Show[ArrayPlot[
MapThread[If[#2, #1, 1] &, {MazeArray1, visitedMatrix}, 2],
ColorRules -> {0 -> White, 1 -> Black, 4 -> LightGray},
ImageSize -> Large],
Graphics[{Red,
Disk[{#2, MazeD1[[2]] - #1} - {0.5, -0.5}, 0.3],
Darker[Green, 0.5],
Disk[{MazeD1[[2]], 1} - {0.5, -0.5}, 0.3]}]],
ArrayPlot[
MapThread[
Which[#1 == 2, 2, #2, #1, True, 1] &, {ReplacePart[
MazeArray1, localVertex -> 2], visitedMatrix}, 2],
ColorRules -> {0 -> White, 1 -> Black, 2 -> Red,
4 -> LightGray, _ -> Black}, ImageSize -> Large,
Epilog ->
If[visitedMatrix[[MazeD1[[1]], 1]], {Darker[Green, 0.5],
Disk[{MazeD1[[2]], 1} - {0.5, -0.5},
0.3]}, {}]]]], {"UpArrowKeyDown" :> (If[
MemberQ[VertexList[AdjGraph1], localVertex + {-1, 0}],
localVertex += {-1, 0};
updateVisibility[localVertex];]),
"DownArrowKeyDown" :> (If[
MemberQ[VertexList[AdjGraph1], localVertex + {1, 0}],
localVertex += {1, 0};
updateVisibility[localVertex];]),
"LeftArrowKeyDown" :> (If[
MemberQ[VertexList[AdjGraph1], localVertex + {0, -1}],
localVertex += {0, -1};
updateVisibility[localVertex];]),
"RightArrowKeyDown" :> (If[
MemberQ[VertexList[AdjGraph1], localVertex + {0, 1}],
localVertex += {0, 1};
updateVisibility[localVertex];])}]]]]]


"Aside" from procedurally generated difficulty levels, I just thought of a multiplayer mode that will be unlike anything we've ever had before, that's why I save my progress in the game I don't just throw it out. Because, synthetic biology is about reprogramming life to accomplish tasks nature didn't originally evolve for, from producing gasoline to constructing entirely new organisms from the ground up. And as those probability distributions "stabilize" across and over "time steps", we know that, we can link abstract math with real-world technology; four-dimensional hyperplatonic solids--polytopes--can provide insight into optimal ways of moving data and arranging switching networks. Suppose we did a maze exploration game where we play mini-golf and, find a new kind of way to represent and ask, how many electrons represent one bit of information; it's somewhere between 10,000 and 100,000. As technology advances, channels etched into semiconductors become smaller--down to about five nanometers--and we start seeing quantum mechanical effects emerge. Can one do something different? Yes. One could use photons instead of electrons. While electrons use doped semiconductor channels, photons require channels of differing refractive indices--photon wires, so to speak. The critical component missing in photonic computing is a photonic switch--an optical transistor. Without this nonlinear switching capability, photonic computing remains fundamentally limited. Photons can exploit the interference effects of light waves, a unique advantage electrons don't readily offer. Interference provides powerful computation methods, particularly for operations like Fourier transforms. Fourier transforms are a specific computation done naturally with interference from light. They represent signals either in time or frequency domains, effortlessly enabling certain computations photonics handles elegantly. Currently, the "line of sight" is like drinking through a straw; it determines visibility of characters and enemies based on obstructing maze walls. The principles of how photons travel and interact through media conceptually mirror visibility computation algorithms within maze games. And I know it's fun, the higher-dimensional polytopes (four-dimensional hyperplatonic solids) that relate conceptually to maze designs. Mazes can be thought of as geometric structures with paths and connections that don't get cut off in all their complexity, analogous to networks or graphs; higher-dimensional geometry could excellently inspire abstract "puzzle" designs, in multi-layered mazes. The maze exploration game already employs randomized maze algorithms like Sierpinski mazes and parallel procedural maze generation could generate realistic imagery or physics that use photon-like models for visibility calculations in maze line-of-sight computations, making visibility dependent on refraction or interference, the optical principles of which might incorporate real-time biologically inspired AI for enemy logic and maze creation "progressively scaled" to player performance and experience level. And the intelligent enemies that track the player, are lifelike and adaptive behaviors that we might "find" if we "procedurally" and endlessly vary the mazes "all over creation". And you can always press the "Shift + R", the case-sensitive restart.
mazeArray = Array[0 &, {100, 100}];
addRandomWalls[array_, wallDensity_] := Module[{newArray = array},
Do[If[(i > 35 && i < 66 && j > 35 && j < 66 && Mod[i, 2] == 0 &&
Mod[j, 2] == 0) ||
(Mod[2*i*j + i + j, 3] == 1 && RandomReal[] < wallDensity),
newArray[[i, j]] = 1],
{i, 100}, {j, 100}
]; newArray]
mazeArray = addRandomWalls[mazeArray, 0.4];
adjGraph = NearestNeighborGraph[Position[mazeArray, 0], {All, 1}];
DynamicModule[{vertex = VertexList[adjGraph][[1]]},
EventHandler[
Dynamic@ArrayPlot[ReplacePart[mazeArray, vertex -> 2],
ColorRules -> {0 -> White, 1 -> RGBColor["#00FFFF"]},
ImageSize -> Large,
PlotRangePadding ->
0.2], {"UpArrowKeyDown" :> (vertex =
If[MemberQ[VertexList[adjGraph], vertex + #1], vertex + #1,
vertex];),
"DownArrowKeyDown" :> (vertex =
If[MemberQ[VertexList[adjGraph], vertex + #2], vertex + #2,
vertex];),
"LeftArrowKeyDown" :> (vertex =
If[MemberQ[VertexList[adjGraph], vertex + #3], vertex + #3,
vertex];),
"RightArrowKeyDown" :> (vertex =
If[MemberQ[VertexList[adjGraph], vertex + #4], vertex + #4,
vertex];)} &[{-1, 0}, {1, 0}, {0, -1}, {0, 1}]]]
Fun is important! Making these dynamic objects available, @Keying Huang. Exploring the cavernous paths of your maze was a delight.

Is it possible for the characters to just communicate via echo-location and develop some sort of "line of sight" further and reach the exit that way?
Those DynamicModules and EventHandlers, it's that knight walk graph @Keying Huang .