Side note
This is a good place to note that Wolfram Language was used and mentioned in a recent preprint by Yuri Matiyasevich (known for his negative solution of Hilbert's tenth problem) and Gleb Beliakov:
Approximation of Riemann's zeta function by finite Dirichlet series: multiprecision numerical approach
where authors also give thanks to our own Oleksandr Pavlyk in the Acknowledgements section.
Visualizations
Recently there were series of forum discussions about interesting visualizations related to simple zeta zeros that are easily done with Wolfram Language. I will give a short summary here, with explanations and code almost word by word from:
All started from a question whether the following is true:
$$\lim_ {y\rightarrow\infty}\zeta(\dfrac{1}{2}+iy)+\dfrac {1} {2}\dfrac {1} {[y/\pi]^{1/2 + iy}} - \sum_{n = 1}^{[y/ \pi]}\dfrac {1} {n^{1/2 + iy}}=0?$$
A simple logic goes along these lines. We have the estimate in the critical strip ( $s = \sigma + it$): $$\zeta(s) = \sum_ {n < N} n^{-s} + \frac{N^{1-s}}{s-1} + O(N^{-\sigma}).$$ Therefore, $$\zeta\left(\frac{1}{2}+it\right) = \sum_ {n < t} \frac{1}{n^{\frac{1}{2}+it}} + O(t^{-1/2}).$$ So $$\lim_ {t \rightarrow \infty} \left | \zeta\left(\frac{1}{2}+it\right) - \sum_{n < t} \frac{1}{n^{\frac{1}{2}+it}} \right| = 0.$$
As a complement to the proof there are some "visual clarifications" (whatever this may mean...) about the behavior of the finite sum of $\zeta$ for a large but fixed ordinate $y\in\mathbb{R}^+$ :
$$S_ y(N)=\sum_ {k=1}^N\frac 1{k^{1/2+iy}}$$
Let's suppose that $y$ is the first ordinate of a nontrivial zero larger than $10000$ and represent all the partial sums $\,S_y(N)$ for $\;N=1\cdots 3183=[y/\pi]\;$ in the complex plane :
Manzoni[n_, y_] := Transpose@{ Re@#, Im@# }&@Accumulate[Range[n]^-(.5 + y I)]
ListLinePlot[Manzoni[3183, Im[ZetaZero[1, 10000]]], Frame -> True,
GridLines -> Automatic, PlotStyle -> Directive[Red, Opacity[.5]],
ImageSize -> 700, PlotRange -> All, AspectRatio -> Automatic]
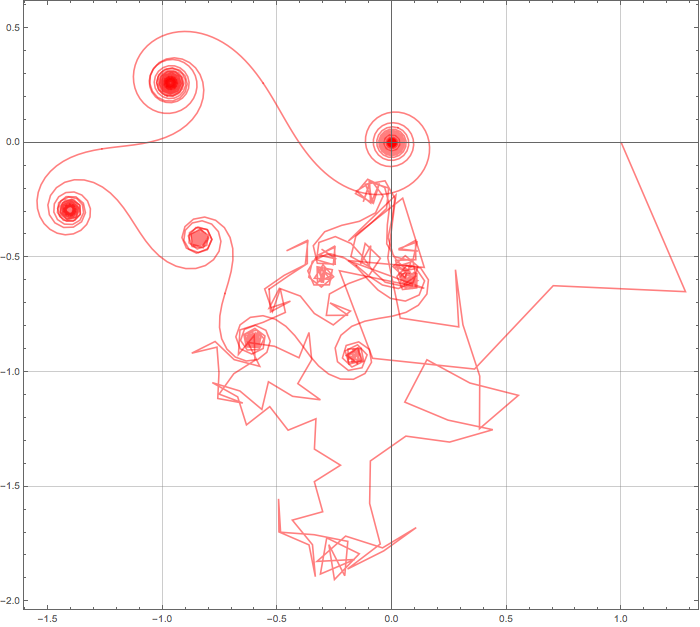
1st point represents $z=S_ y(1)=1$ and 2nd $S_ y(2)=1+\dfrac {2^{-iy}}{\sqrt{2}}$ and so on up to 3183 representing $S_ y(3183)$ very near to $0$.
The picture shows figures looking like Cornu (or Euler) spirals. Let's justify this :
the sum $S_ y(N)$ is obtained by addition of $\,\displaystyle \frac 1{k^{1/2+iy}}=\frac {e^{-iy\log(k)}}{\sqrt{k}}\,$ terms.
The next term will thus be $\,\displaystyle \frac {e^{-iy\log(k+1)}}{\sqrt{k+1}}$.
Now for $k\gg 1$ the denominator will change only slightly while the change of phase of the numerator will be $\;\delta=-y\;(\log(k+1)-\log(k))=-y\,\log(1+1/k)\approx -\dfrac yk$.
$\delta\approx -\dfrac {y}k$ gives a special role to the values of $k$ such that $\dfrac yk\approx f\pi$ with $f$ integer :
- for $f=2m$ (i.e. $k=\left[ \frac y{2m\pi}\right]$) we have $\,\delta\approx -2m\pi\,$ : for values of $k$ near of $\left[ \frac y{2m\pi}\right]$ the terms have nearly the same phase and their addition will nearly give a straight line (see f=2, f=4, and so on on the picture)
- for $f=2m+1$ (i.e. $k=\left[ \frac y{(2m+1)\pi}\right]$) we have $\,\delta\approx -(2m+1)\pi\,$ : for values of $k$ near of $\left[ \frac y{(2m+1)\pi}\right]$ two consecutive terms nearly cancel each other and that's what is happening in the middle of the 'nodes' f=1, f=3, f=5 and so on.
Let's zoom the center of the final node:
ListLinePlot[Manzoni[3183, Im[ZetaZero[1, 10000]]], Frame -> True,
GridLines -> Automatic, PlotStyle -> Directive[Red, Opacity[.4]],
PlotRange -> .0008 {{-1, 1}, {-1, 1}}, AspectRatio -> Automatic]
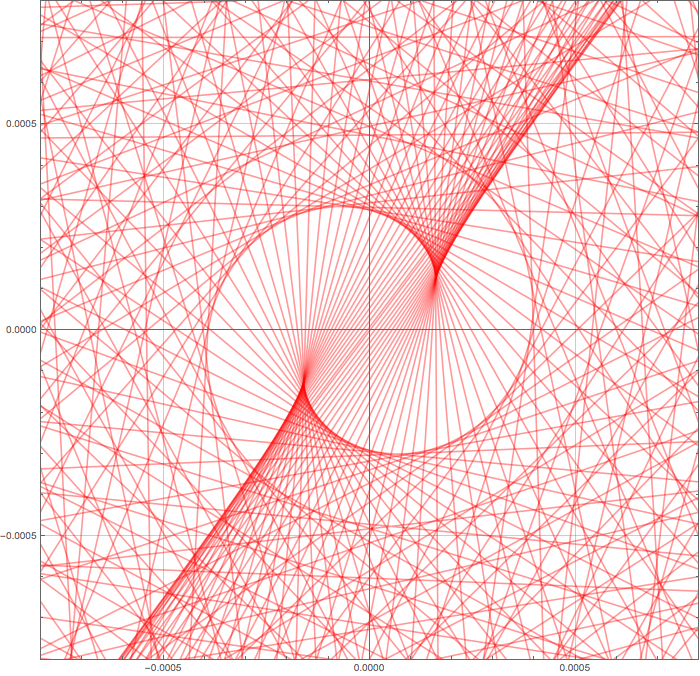
The line nearly crossing the origin is obtained with the term $k=3183=\left[ y/\pi\right]$ while the line at its left and right came from $k=3182$ and $k=3181$ respectively. The value $S_ y(3183)$ itself is far out of the picture (say $12$ or more times higher) while $S_ y(3182)$ is far at the bottom on the other side. Taking the middle of these two values should bring us not too far from our target even if the different partial sums $S_ y(N)$ don't really 'go down to $0$' ! (they merely turn around). All this explains (but doesn't prove) that an excellent approximation for $\zeta$ may be obtained (near the zeros at least) with the formula :
$$\zeta\left(\frac 12+iy\right)\approx \sum_ {n=1}^{[y/ \pi]}'\frac{1}{n^{1/2+iy}}=-\frac 1{2\,[y/\pi]^{1/2+iy}}+\sum_ {n=1}^{[y/ \pi]}\frac{1}{n^{1/2+iy}}$$
(numerically the absolute error appears majored by $\dfrac{4.5}{y^{3/2}}$ in the range $(10,10000)$, and probably for larger values, while the initial sum from the question was majored by $\dfrac{0.9}{y^{1/2}}$)