You have encountered the limitations of using machine precision calculations in the internal numerical algorithms for MeijerG. Though I am not sure why you are using ListLinePlot, here is an example using Plot with its WorkingPrecision option set to a higher non-MachinePrecision value. Also note that I changed your floating point value to an exact number so that the floating point value would not conflict with the higher precision computations specified by the WorkingPrecision option.
Plot[27235615/85563208 MeijerG[{{0, 1/2}, {}}, {{0, 1/2}, {-(1/2)}}, x^2],
{x, -24, 0},
PlotRange -> All,
WorkingPrecision -> 50]
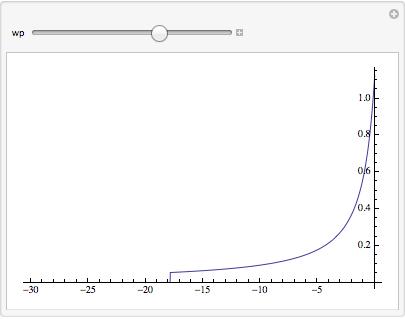
However, the behavior of where the "cliff" discontinuity appears in the function is a bit odd and depends on what the value of the WorkingPrecision option is. So it appears not to be a branch cut crossing, but it is unclear what is happening in the internal algorithm that is causing it to truncate and return a value of 0 to the left of the WorkingPrecision-dependent discontinuity.
Take a look at the following to see how the discontinuity is depending on the value of WorkingPrecision :
Manipulate[
Plot[27235615/85563208 MeijerG[{{0, 1/2}, {}}, {{0, 1/2}, {-(1/2)}},
x^2], {x, -30, 0}, PlotRange -> All, WorkingPrecision -> wp],
{wp, 30, 200}, ContinuousAction -> False]
Here are two screenshots of this manipulate at different values of the WorkingPrecision slider:
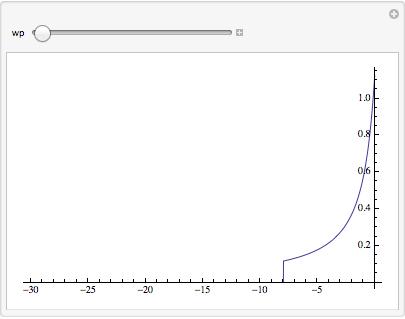
and