Message Boards Message Boards

1
|
2806 Views
|
3 Replies
|
5 Total Likes
View groups...
Share
Share this post:

Problem or bug with MeijerG function (sharp jump)?

gang guo
Posted 11 years ago

Hi, I run into the MeijerG function with the specific case

ListLinePlot[{Table[{x, 0.31830988618379064* MeijerG[{{0, 1/2}, {}} , {{0, 1/2}, {-1/2}} , x*x]}, {x, -24, 0, 1}]}, PlotRange -> All]

However, the curve is not continuous. Can anybody help to give some hints about the problem?
POSTED BY: gang guo
3 Replies
Sort By:

I think this needs a special-functions expert. The function does go to zero abruptly and stay there. 

In[1]:= MeijerG[{{0,1/2},{}},{{0,1/2},{-1/2}},x*x]  /. {{x->-5.9},{x->-6},{x->-6.1},{x->-6.2},{x->-6.3},{x->-6.4}} //N
Out[1]= {0.490874,0.392699,1.5708,0.,0.,0.} 

In[4]:= qq = 0.3183098861837906400000000000000000000000000;
In[5]:=Plot[{qq*MeijerG[{{0, 1/2}, {}}, {{0, 1/2}, {-1/2}}, x*x]}, {x, -24, 0} , PlotRange -> All, WorkingPrecision -> 25]

enter image description here
POSTED BY: Bruce Miller

You have encountered the limitations of using machine precision calculations in the internal numerical algorithms for MeijerG. Though I am not sure why you are using ListLinePlot, here is an example using Plot with its WorkingPrecision option set to a higher non-MachinePrecision value. Also note that I changed your floating point value to an exact number so that the floating point value would not conflict with the higher precision computations specified by the WorkingPrecision option.

Plot[27235615/85563208 MeijerG[{{0, 1/2}, {}}, {{0, 1/2}, {-(1/2)}}, x^2], 
{x, -24, 0}, 
PlotRange -> All, 
WorkingPrecision -> 50]

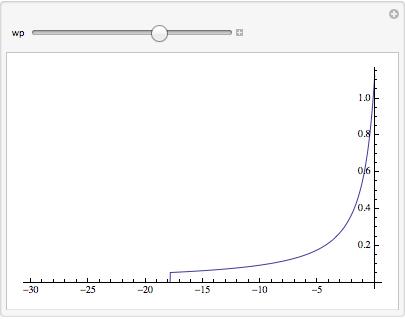
However, the behavior of where the "cliff" discontinuity appears in the function is a bit odd and depends on what the value of the WorkingPrecision option is. So it appears not to be a branch cut crossing, but it is unclear what is happening in the internal algorithm that is causing it to truncate and return a value of 0 to the left of the WorkingPrecision-dependent discontinuity.

Take a look at the following to see how the discontinuity is depending on the value of WorkingPrecision :

Manipulate[
 Plot[27235615/85563208 MeijerG[{{0, 1/2}, {}}, {{0, 1/2}, {-(1/2)}}, 
    x^2], {x, -30, 0}, PlotRange -> All, WorkingPrecision -> wp],
 {wp, 30, 200}, ContinuousAction -> False]

Here are two screenshots of this manipulate at different values of the WorkingPrecision slider:

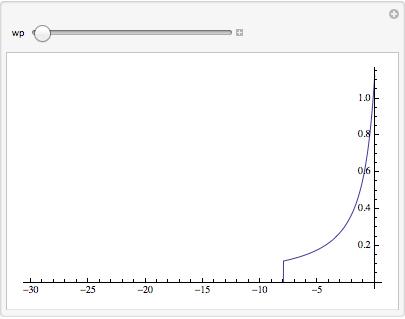
enter image description here

and

enter image description here
POSTED BY: David Reiss

A developer I asked said this cliff comes from cancellations while summing the series.

His suggestions were higher Working Precision (which David showed nicely) and using a simpler-function version of the expression. 

 In[1]:= fsfe=FullSimplify[
            FunctionExpand[ MeijerG[{{0,1/2},{}},{{0,1/2},{-1/2}},x*x]  ],  {x<0} ] 

 Out[1]= ( Pi (-1+E^x^2 (1+Erf[x] )))/x 

 In[2]:= qq = Rationalize[0.318309886183790640, 0]; 

 In[3]:= Plot[ qq * fsfe, {x,-24,0}, PlotRange->All, WorkingPrecision->20, AxesOrigin->{0,0}]

Here, the WorkingPrecision->20 eliminated one artifact in the curve.

enter image description here

The original code can be modified simply. Note the N[.. ,20] around the MeijerG call.
That was enough extra precision to prevent cancellations at larger x's. 

In[7]:= ListLinePlot[{ Table[{x, qq* N[MeijerG[{{0, 1/2}, {}} , {{0, 1/2}, {-1/2}} , x*x], 20] }, {x, -24, 0, 1}] }, PlotRange -> All]

enter image description here
POSTED BY: Bruce Miller
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract