
Some years back, I saw a pair of excellent blog posts on The Rolling Shutter Effect (here and here). The Rolling Shutter Effect is a form of distortion that can appear in photographs taken on a phone, since phone cameras typically capture frames by scanning across a scene horizontally/vertically over a period of time instead of capturing the entire scene at the same instant. When the subject of the photograph is static or slow-moving, this method of recording an image does not cause a problem. But for a fast-moving object such as an airplane propeller, a rolling shutter can produce fascinating forms of distortion. For example, here's an image of an airplane propeller captured by a Pixel 3:
 Source: Wikipedia
Source: Wikipedia
In order to model the effect, I started with a plot of an "airplane propeller." I used the polar equation r = 3 cos(5θ):
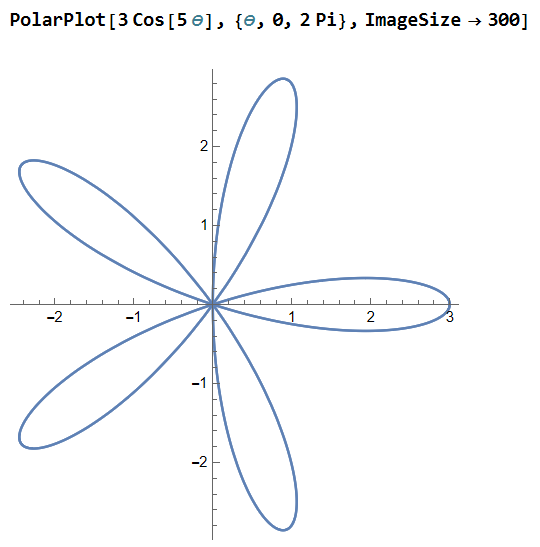
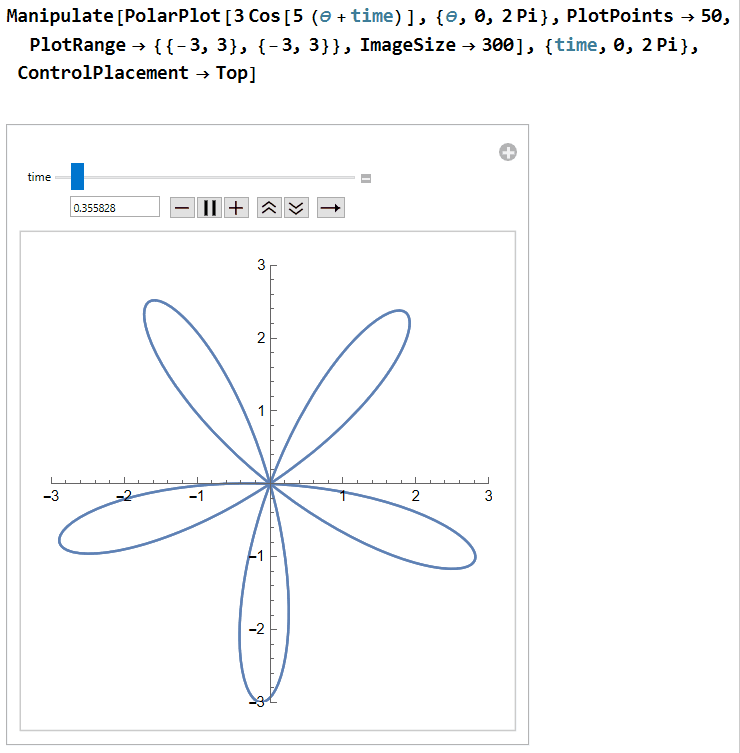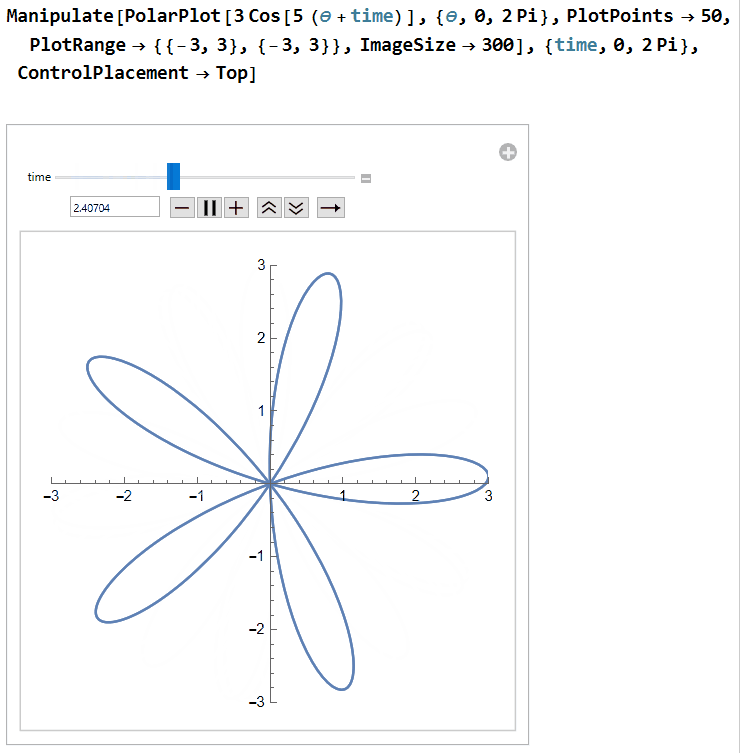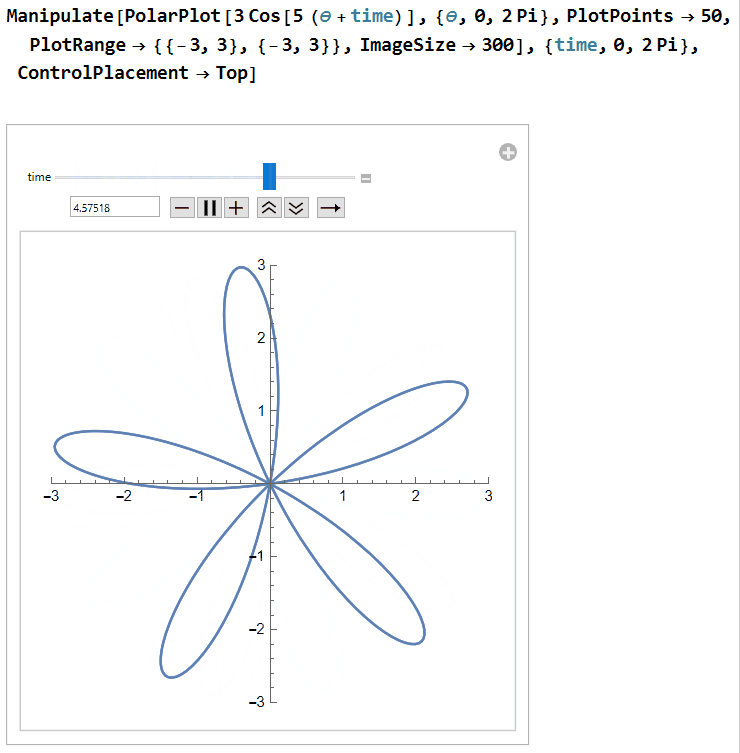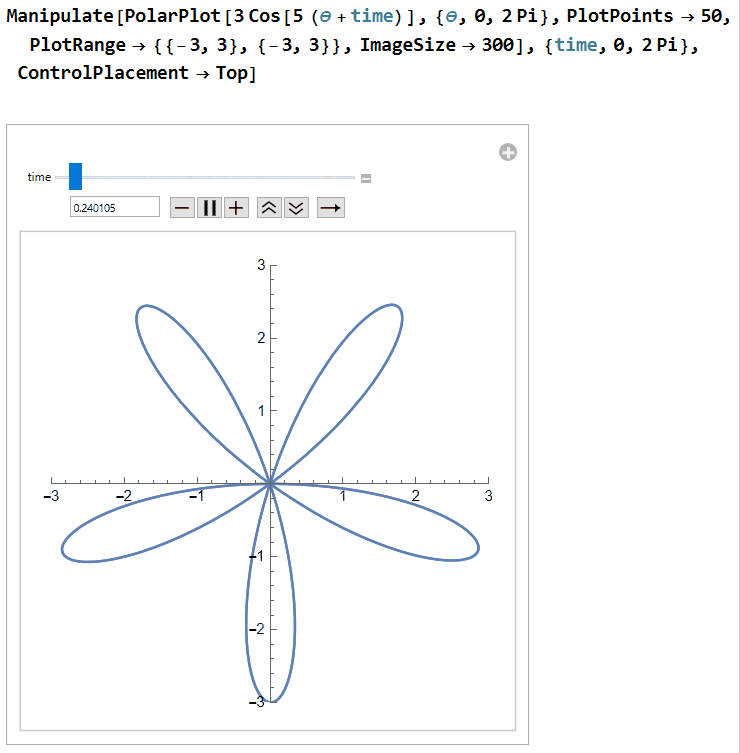
Now we can make the make the propeller spin by writing r = 3 cos(5(θ+time)) for some fixed value "time":
Next, let's get the rolling shutter into the mix. We'll start with a horizontal line at y = 3 that moves down as time progresses. This can be written as y= 3 - time. We will also adjust our propeller equation to be r = 3 cos(5(θ+time/s)). The newly introduced s is a factor that is meant to represent the fact that the rate at which the shutter moves may differ from the rate at which the propeller rotates. We are putting the s with the propeller since we are treating the speed of our rolling shutter as a constant while the speed of the propeller may vary:
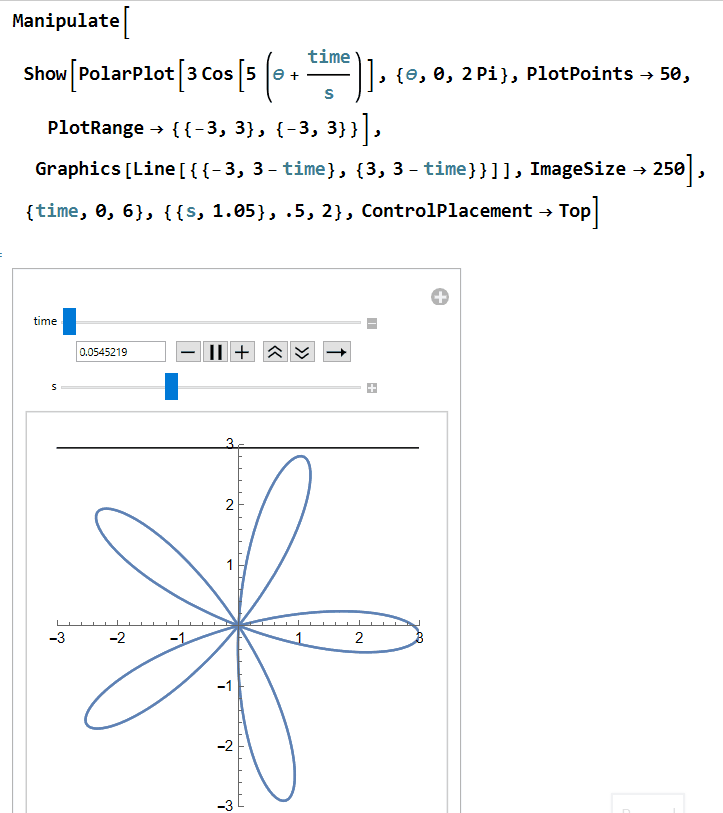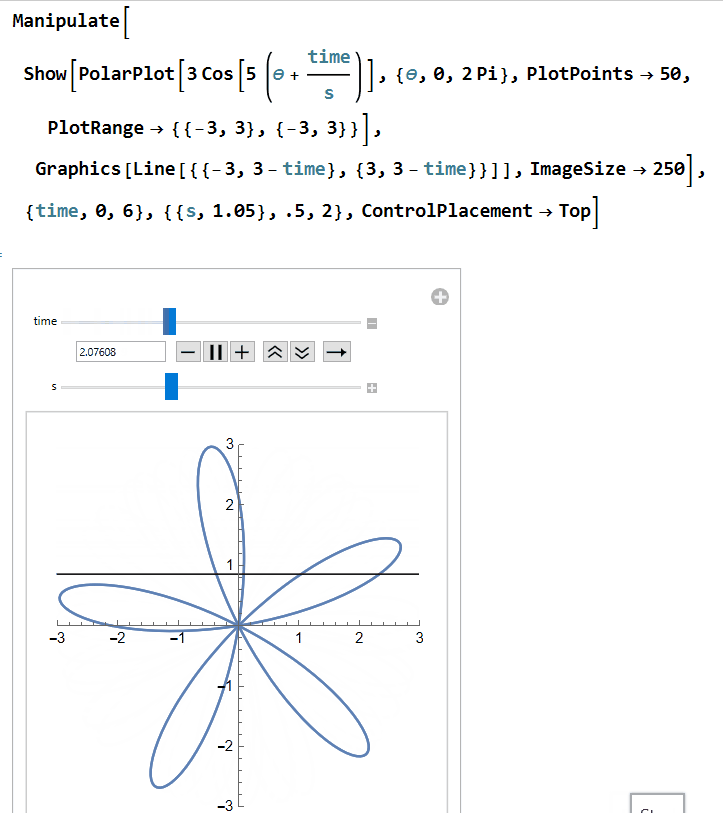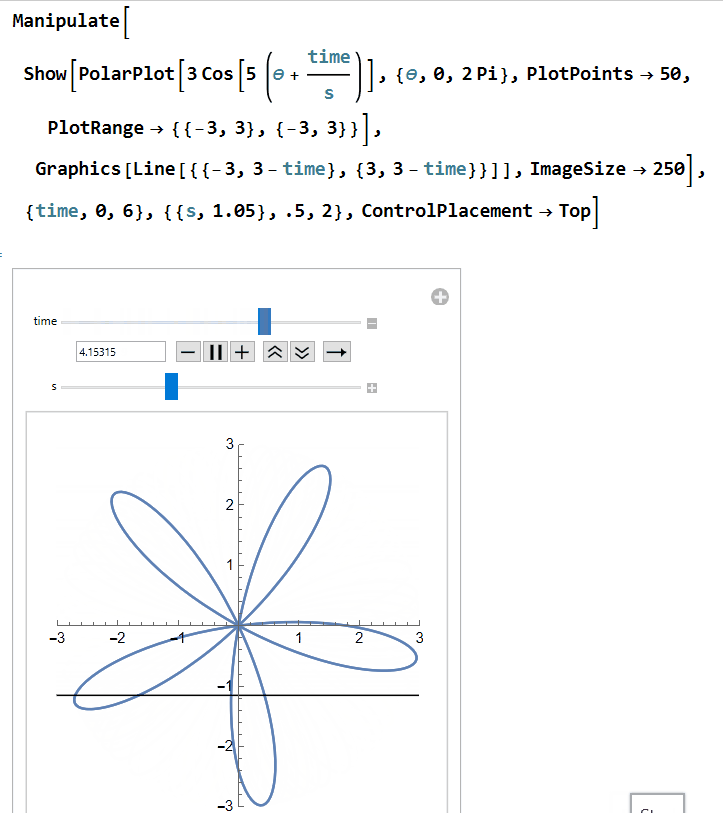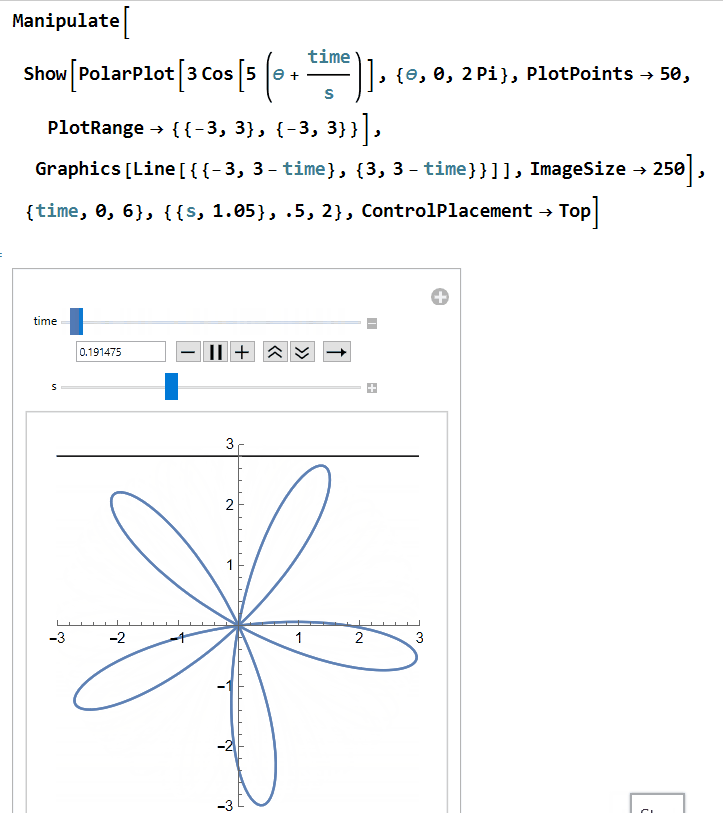
In order to simulate The Rolling Shutter Effect, it will be helpful to switch to a Cartesian plot instead of a polar plot. First rewrite r = 3 cos(5(θ+time/s)) as 1 = ((3 cos(5θ))/r). Then substitute in r = Sqrt[x^2+y^2] and θ = arctan(x,y) to get 1 = ((3 cos(5(arctan(x,y)+time/s)))/Sqrt[x^2+y^2]) . We can plot this using a contour plot:
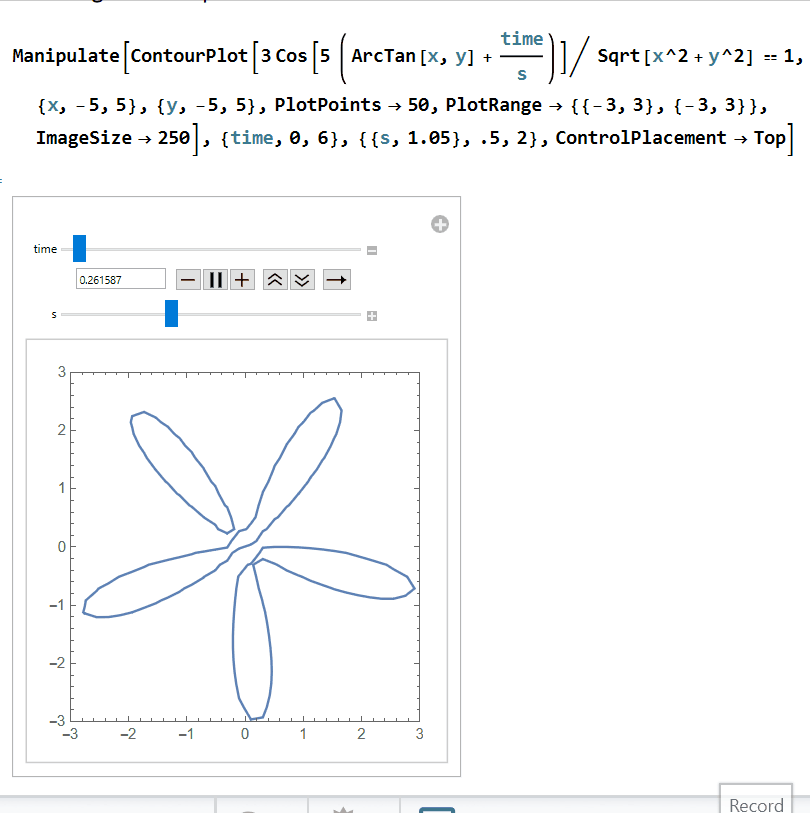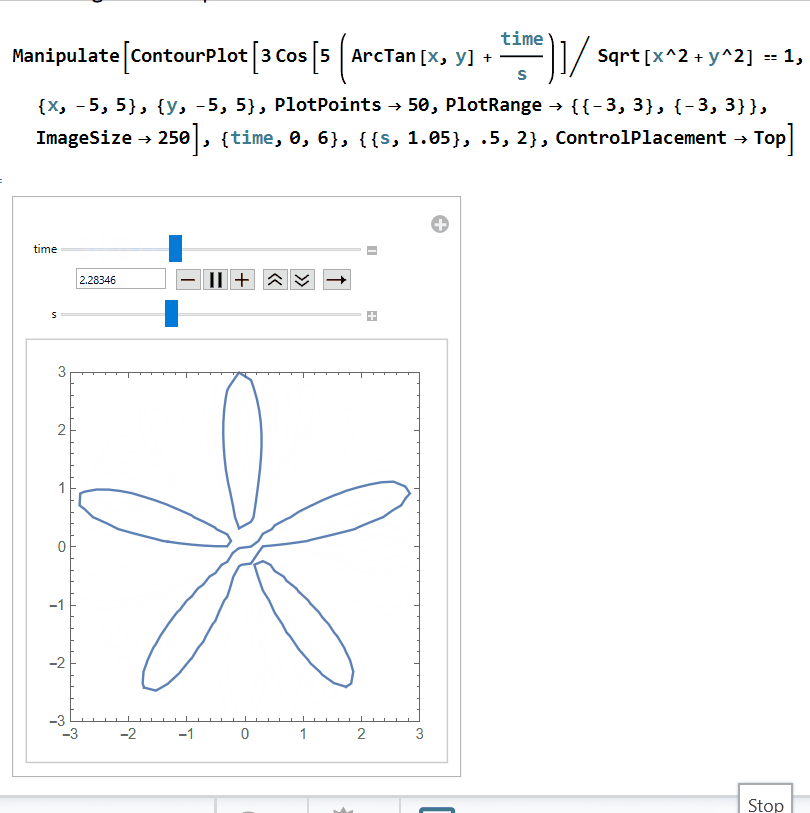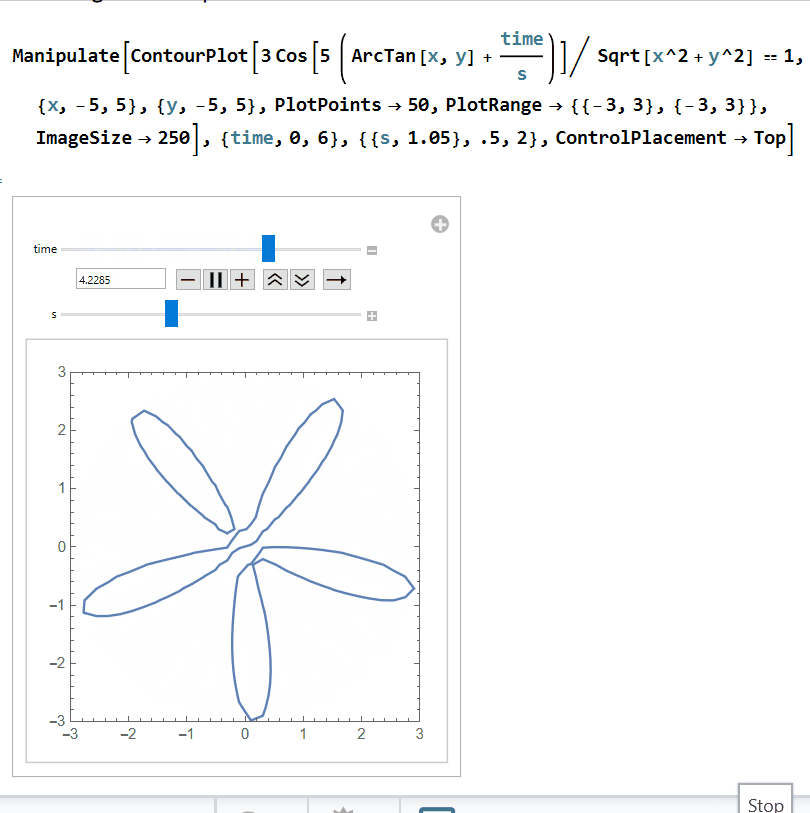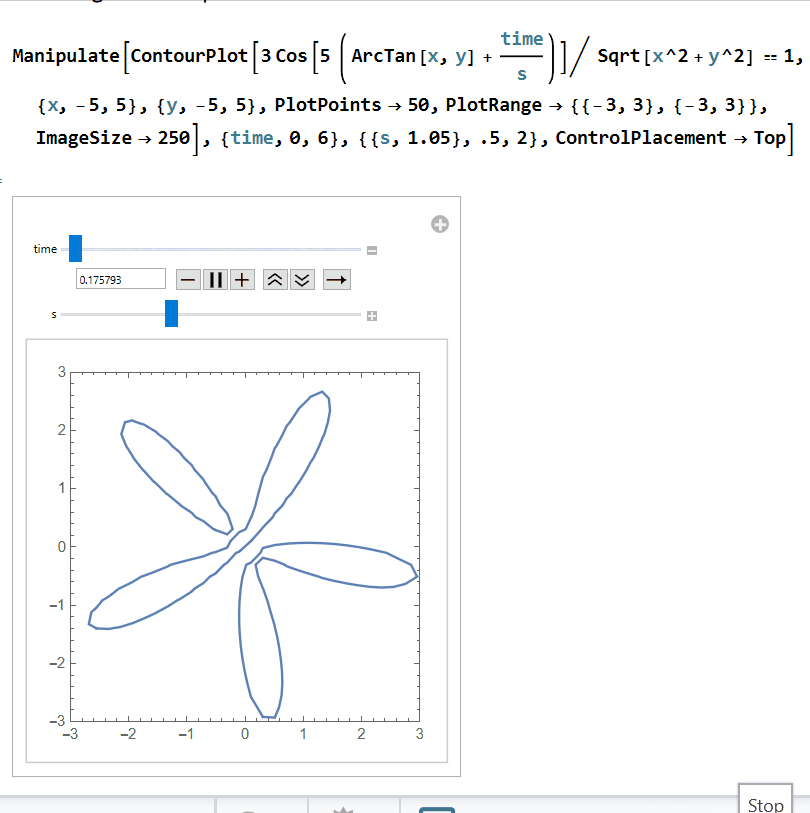
Finally, we need to find the "distorted" plot that is left behind after the shutter passes. We are looking for the locus of points intersecting the shutter y = 3 - time. Solving for time gives us time = 3 - y. Further, in polar coordinates, y = r sin(θ), so time = 3-r sin(θ). In rectangular coordinates, we also substitute in r = Sqrt[x^2+y^2] and θ = arctan(x,y). Let's substitute all of this into our contour plot from above, (3 cos(5 (arctan(x,y)+time/s)))/Sqrt[x^2+y^2]=1:
(3 cos(5 (arctan(x,y)+(3 - Sqrt[x^2+y^2] sin(arctan(x,y)))/s)))/Sqrt[x^2+y^2]=1
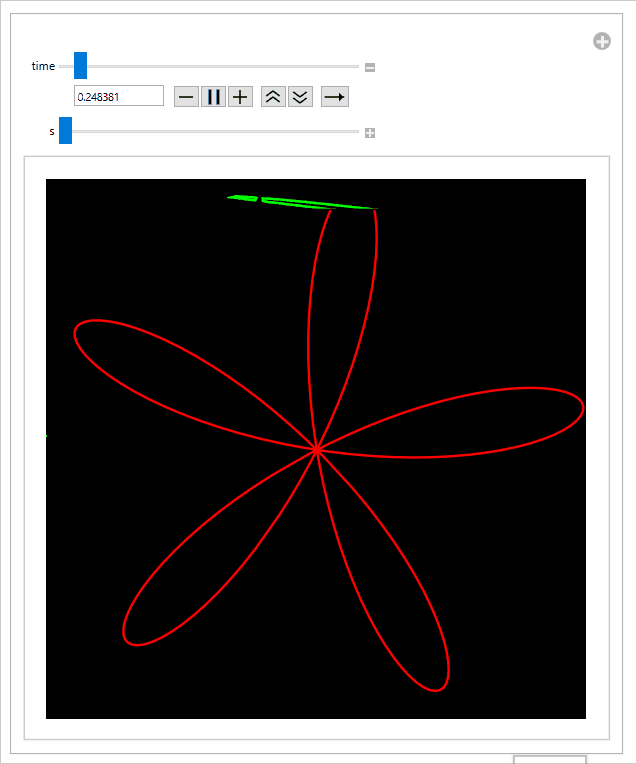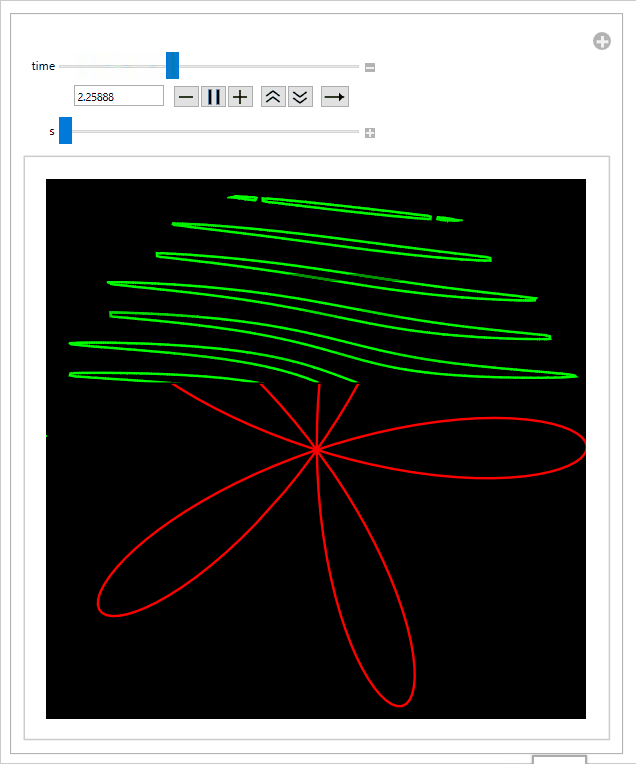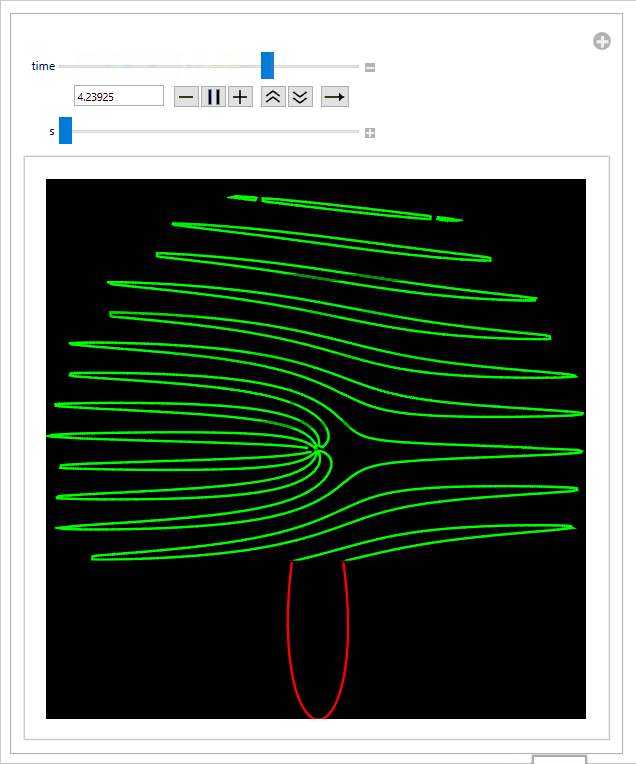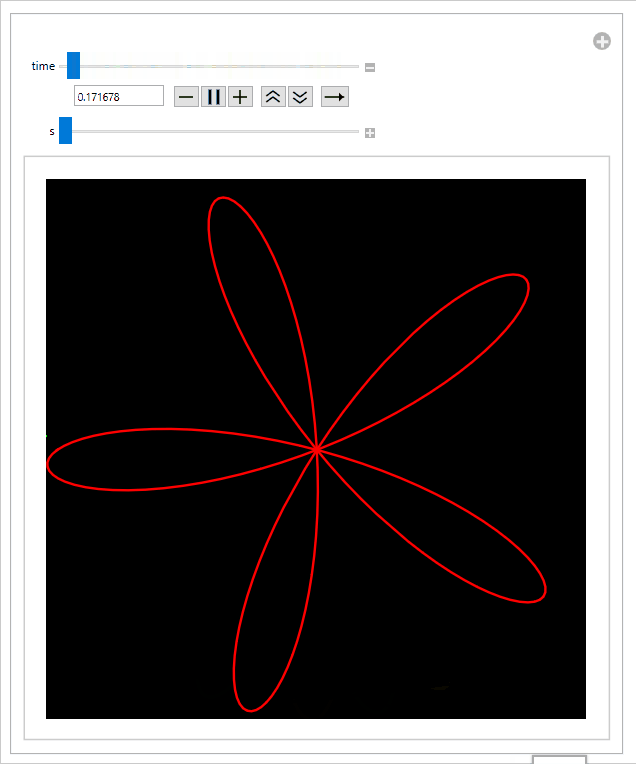
This looks like a mess, but let's plot an example for s = 0.8 to see if the result appears reasonable:
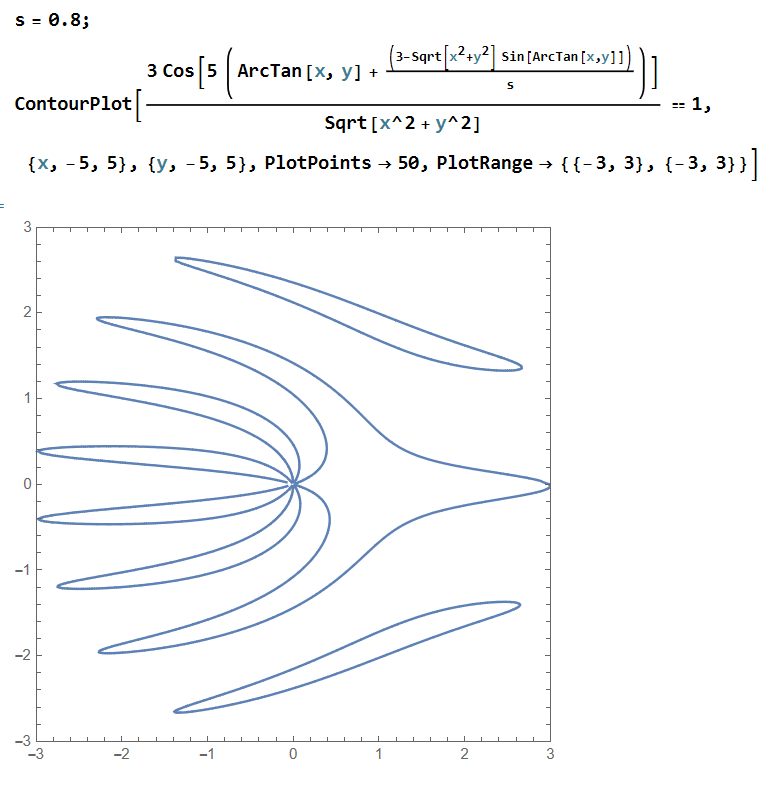
This looks exactly like the type of plot we expect. Let's put it all together to see. Here's the code with some better styling and some optimization to make sure that the Manipulate precomputes the distorted image:
Manipulate[
Graphics[{Dynamic@
First@ContourPlot[(
3 Cos[5 (
ArcTan[x, y] + (3 - Sqrt[x^2 + y^2] Sin[ArcTan[x, y]])/
s)])/Sqrt[x^2 + y^2] == 1, {x, -5, 5}, {y, -5, 5},
PlotPoints -> 50, ContourStyle -> Green,
PlotRange -> {{-3, 3}, {-3, 3}}],
Dynamic@First@Graphics[{Black, Rectangle[{-3, 3 - time}, {3, -3}]}],
Dynamic@
First@ParametricPlot[
3 Cos[5 (\[Theta] + time/s)] {Cos[\[Theta]],
Sin[\[Theta]]}, {\[Theta], 0, Pi}, PlotStyle -> Red,
RegionFunction -> Function[{x, y, \[Theta]}, y < 3 - time]],
Dynamic@First@Graphics[Line[{{-3, 3 - time}, {3, 3 - time}}]]},
Axes -> False, PlotRange -> {{-3, 3}, {-3, 3}},
Background -> Black], {time, 0, 6}, {{s, 0.8}, 0.3, 4},
ControlPlacement -> Top]
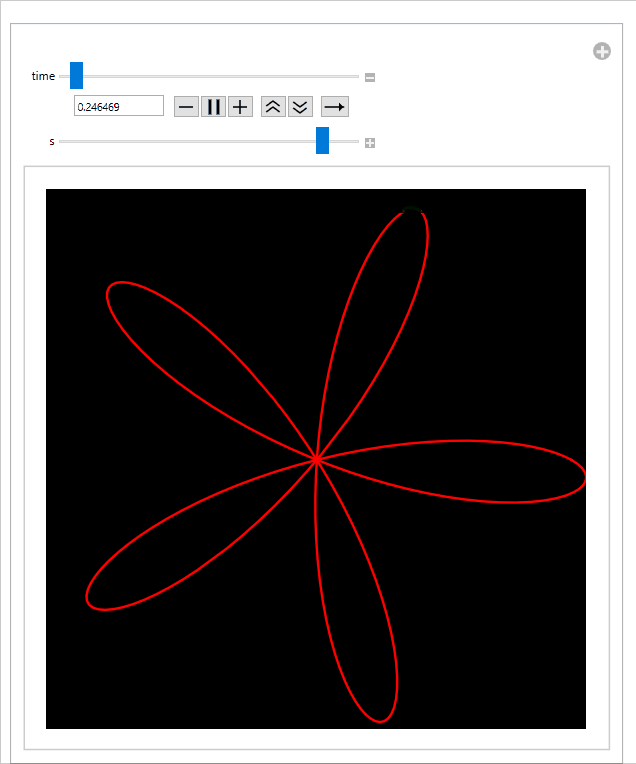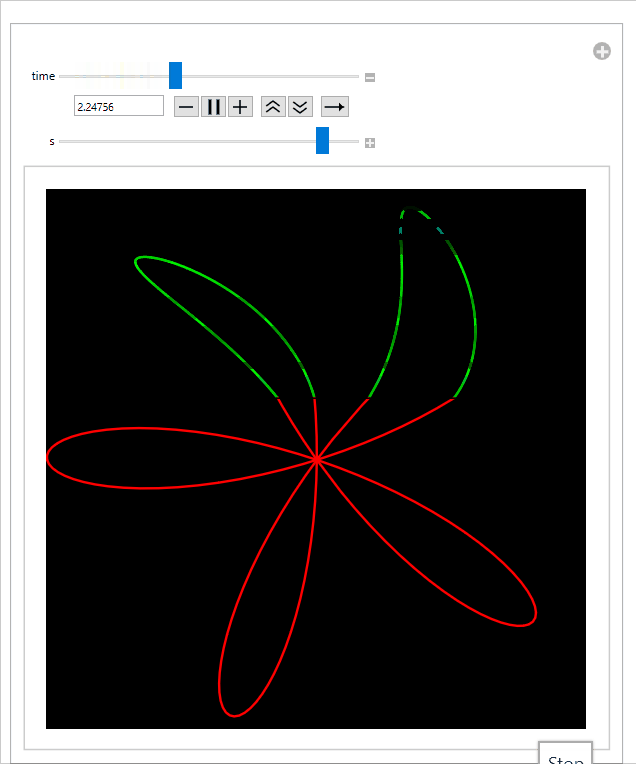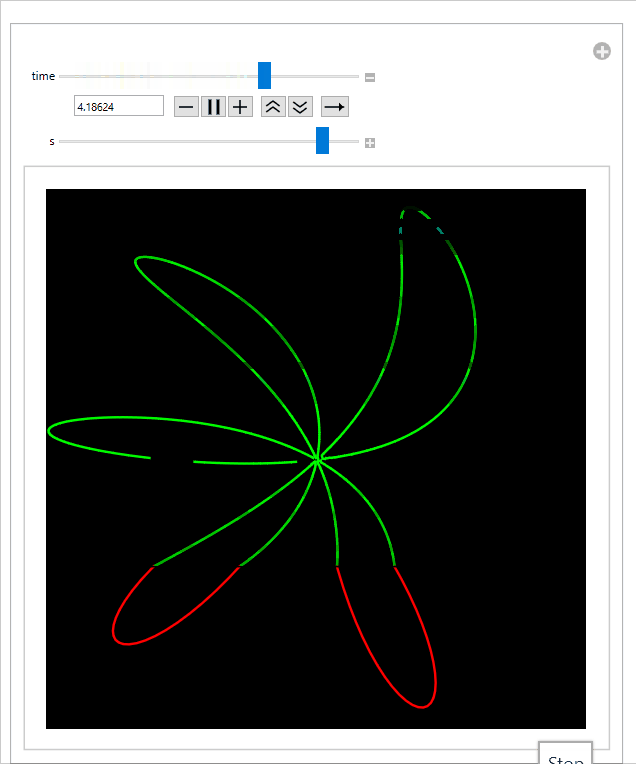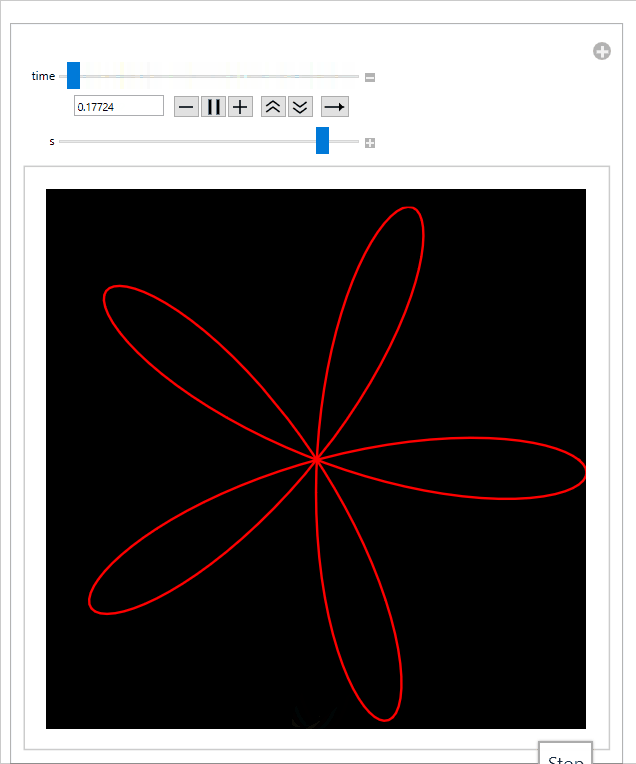
And the final animation:
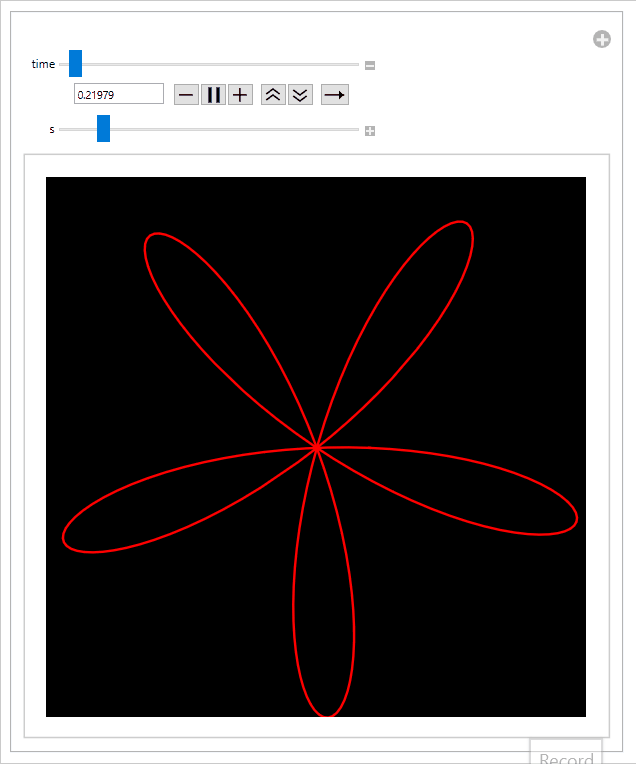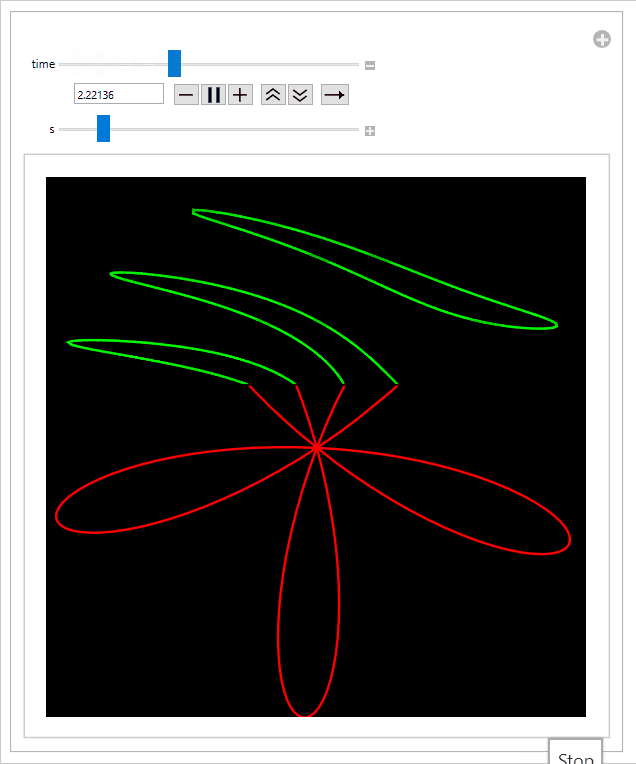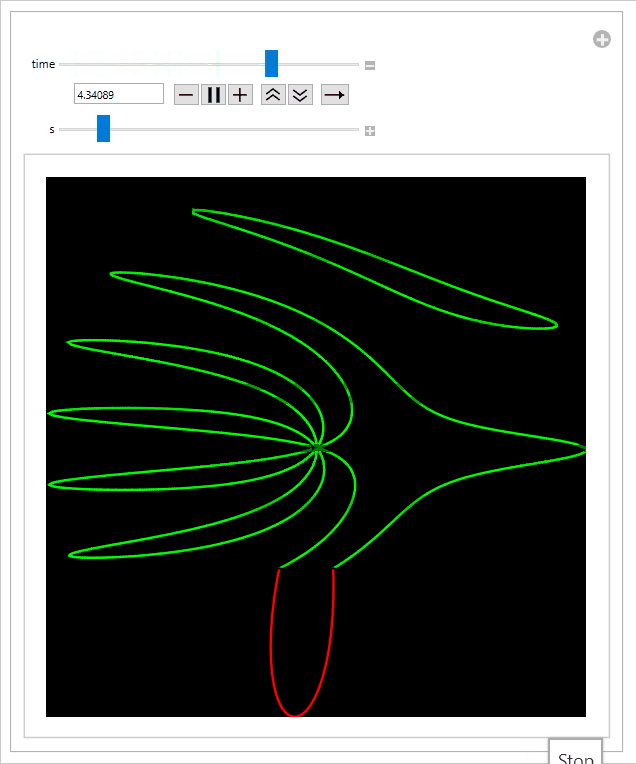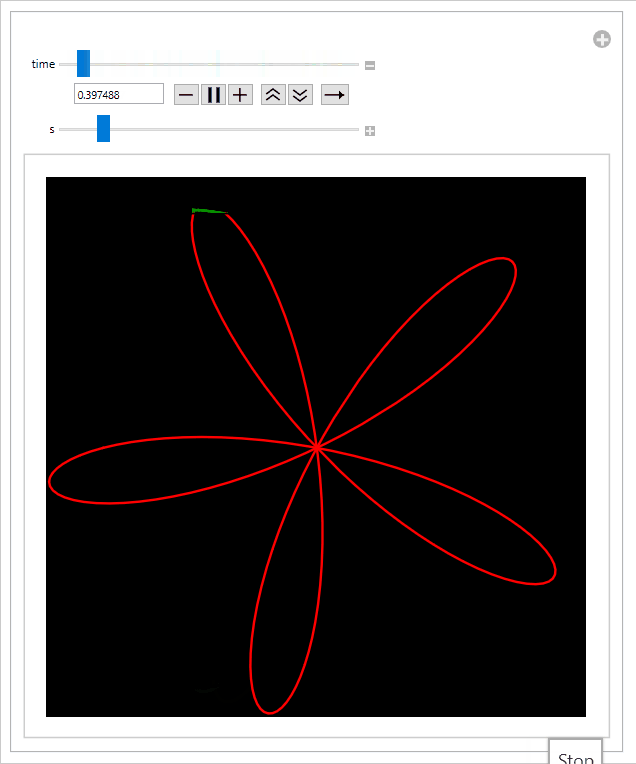
Sliding the s-slider to the left speeds up the propeller relative to the speed of the rolling shutter, thus increasing the intensity of the effect:
Sliding the s-slider to the right slows down the propeller, which decreases the amount of distortion:
Download Notebook
I've included my original notebook if you'd like to play with the code yourself.