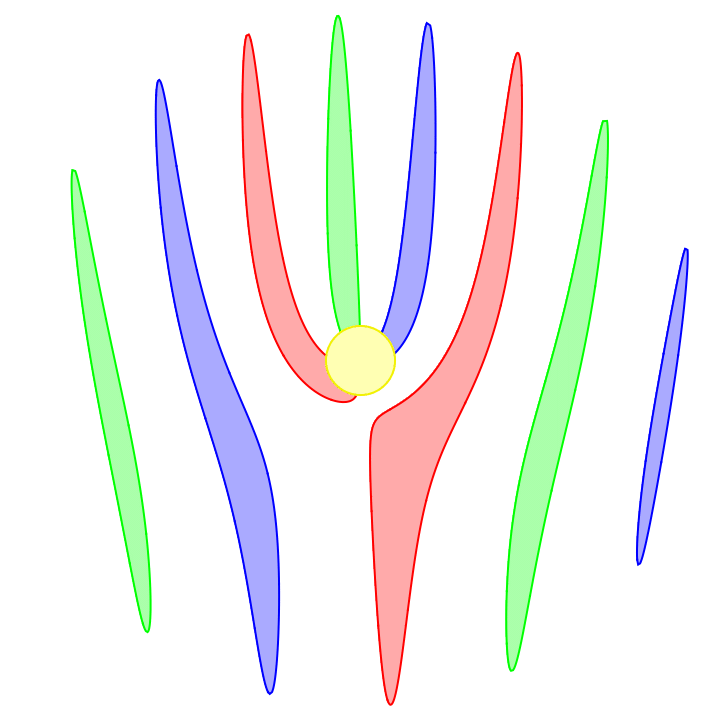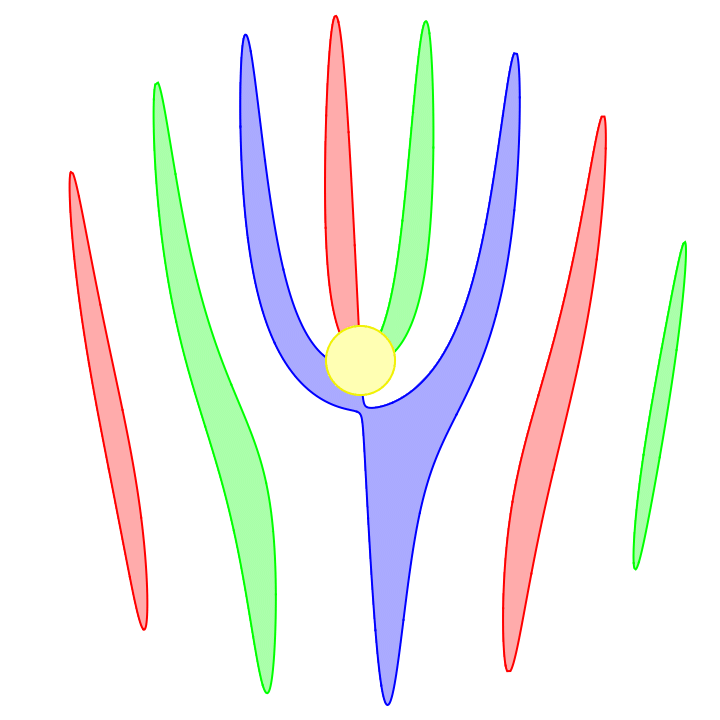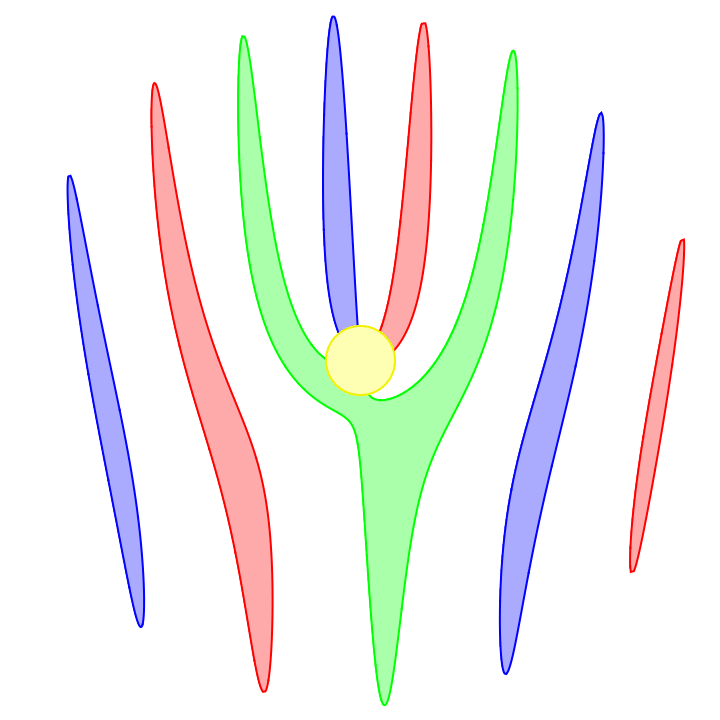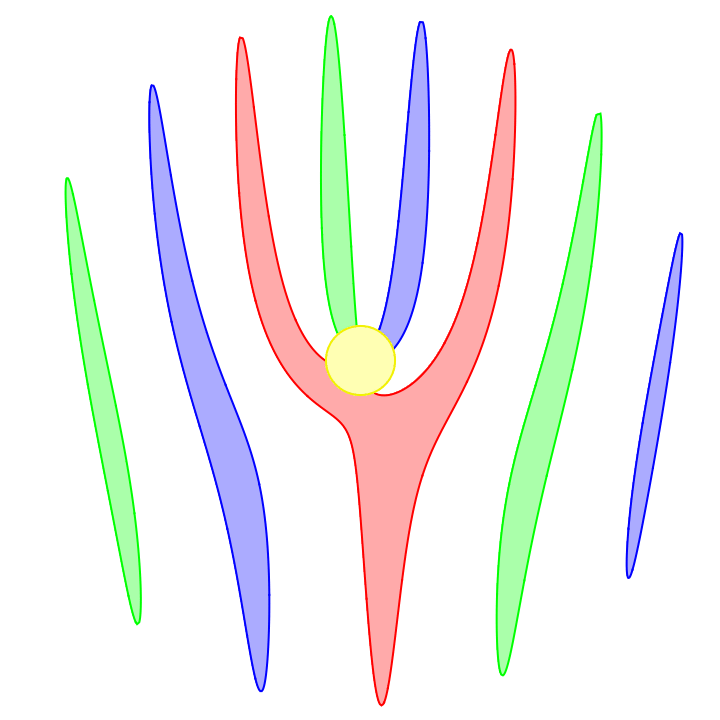
Most cell phone cameras capture an image using a rolling shutter. This means an image is not captured all at once but rather is captured with a scrolling line, either horizontally or vertically.
This scrolling is fast and in most situations is not noticeable. But for a scene with motion rivaling the camera's scroll speed, things will look distorted. A fast moving car might look sheared, squished, or stretched, and a spinning propeller looks quite strange.
To see how the strange pattern in the above image appears, let's start off by idealizing a propeller as a trifolium in polar coordinates:
propeller[θ_] := Sin[3θ + π/2];
PolarPlot[propeller[θ], {θ, 0, 2π}]

Now as the scrolling happens, each scroll line will be looking at a different rotated version of the propeller. In polar coordinates that's just a shift in angle, e.g. propellar[θ + shift]. If we assume the camera scrolls in the x (horizontal) direction at a constant speed, then the shift value will be a constant times x.
For this example we'll assume the propeller makes 2.25 revolutions in the time the camera completes the scrolling. Now that we've mixed polar and Cartesian, we'll switch to RegionPlot:
revs = 2.25;
plot = With[{r = Sqrt[x^2 + y^2], θ = ArcTan[x, y]},
RegionPlot[
r <= propeller[θ - π*revs*x],
{x, -1, 1}, {y, -1, 1},
Frame -> None,
PlotPoints -> 100
]
]
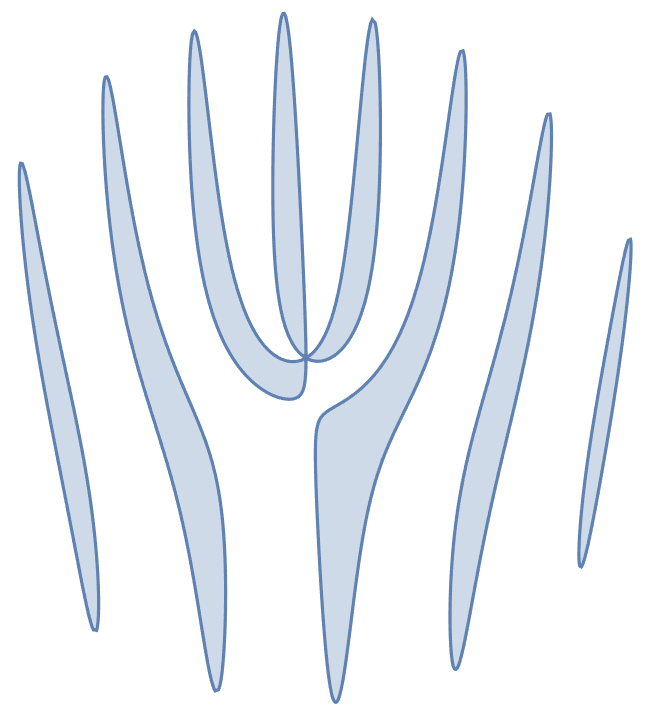
We can get an intuitive feel for why this happens by simulating the rolling shutter ourselves:
Manipulate[
Show[
plot,
Graphics[{{EdgeForm[], White, HalfSpace[{-1, 0}, {t, 0}]},
{Thick, Black, InfiniteLine[{{t, 0}, {t, 1}}]}}],
PolarPlot[
propeller[θ - π*revs*t],
{θ, 0, π},
RegionFunction -> Function[{x, y, r, θ}, x > t],
PlotStyle -> Red
]
],
{t, -1, 1}
]

Lastly, we can simulate what a video of a spinning propeller would look like. Essentially each frame of the video would contribute a constant shift to θ (unlike the how the scrolling's shift depends on x).
Monitor[
plots = With[{r = Sqrt[x^2 + y^2], θ = ArcTan[x, y]},
Table[
RegionPlot[
r <= propeller[θ - π*revs* x + α],
{x, -1, 1}, {y, -1, 1},
Frame -> None
PlotPoints -> 100
],
{α, 0, 2π, π/20}
]
];,
α
]
Omitting the code for styling and coloring each propeller differently, here's the result: