Hi, I am trying to go from a set of points to a piecewise function.
I use the following command, but I get only one large step , in the step-wise function.
points = {{1004.9591023489934`,
213.55957424496637`}, {998.3619966442955`,
297.1229131711409`}, {996.1629614093961`,
275.13256082214764`}, {989.5658557046982`,
386.55034605704714`}, {982.96875`,
360.1619232382552`}, {971.9735738255035`,
298.58893666107394`}, {963.1774328859062`,
305.186042365772`}, {954.3812919463089`,
270.00147860738275`}, {945.5851510067116`,
340.3706061241612`}, {941.1870805369128`,
296.3899014261747`}, {934.5899748322149`,
329.3754299496645`}, {927.9928691275168`,
274.3995490771813`}, {921.3957634228188`,
307.38507760067125`}, {910.4005872483222`,
305.186042365772`}, {908.201552013423`,
351.3657822986579`}, {890.6092701342284`,
210.62752726510075`}, {881.8131291946311`,
417.3368393456377`}, {864.2208473154362`,
245.81209102348998`}, {855.4247063758389`,
344.76867659395987`}, {848.827600671141`,
285.394725251678`}, {842.2304949664431`,
377.7542051174498`}, {826.8372483221477`,
265.603408137584`}, {820.2401426174498`,
274.3995490771813`}, {809.2449664429531`,
377.7542051174498`}, {802.6478607382551`,
252.40919672818814`}, {793.8517197986578`,
267.80244337248337`}, {785.0555788590605`,
393.14745176174506`}, {769.66`, 168.85`}, {758.67`,
28}, {745.4729446308726`,
175.44296350671158`}, {730.0796979865772`,
346.96771182885925`}, {723.4825922818793`,
410.7397336409398`}, {719.0845218120807`,
274.3995490771814`}, {710.2883808724833`,
285.39472525167804`}, {705.8903104026846`,
252.40919672818808`}, {692.6960989932886`,
289.7927957214767`}, {688.29802852349`,
415.13780411073844`}, {677.3028523489934`,
313.9821833053693`}, {664.1086409395974`,
190.83621015100687`}, {655.3125000000001`,
443.72526216442975`}, {646.5163590604027`,
270.0014786073827`}, {639.9192533557048`,
248.01112625838942`}, {631.1231124161075`,
327.17639471476525`}, {617.9289010067115`,
373.3561346476512`}, {611.3317953020135`,
338.17157088926194`}, {598.1375838926175`,
221.6227034395975`}, {589.3414429530202`,
404.1426279362418`}, {580.5453020134229`,
259.00630243288606`}, {573.9481963087248`,
305.186042365772`}, {571.7491610738256`, 360.1619232382552`}};
draupnerfun[t_] :=
Piecewise[
Table[{points[[i, 2]], points[[i, 1]] > t}, {i, Length[points]}], 0]
p0 = Plot[draupnerfun[t], {t, 570, 1005}]
and I got this
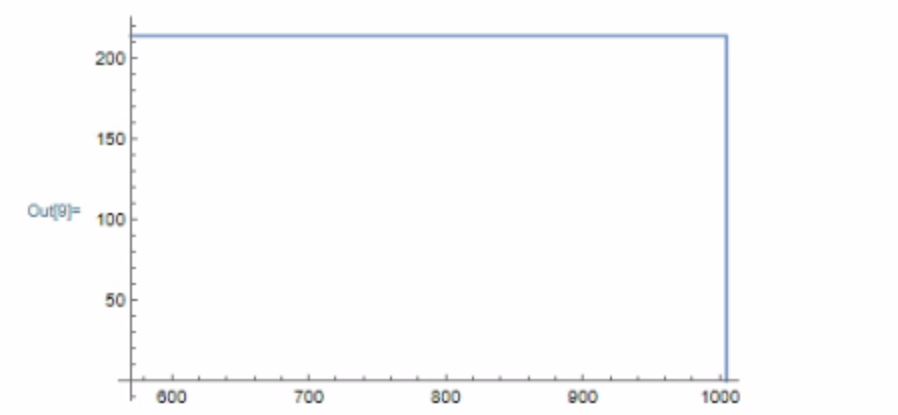
Evidently, this didn't work. What is wrong with this command?
Thanks