Merge H7 and H8 to substitute

Since there are at least two ways to separate tiling, one is H8 and H7, and the other is H8 and alternative H7. So here I tried to merge H7 and H8 together to avoid "disagreement" or "difference", and to see if we can get the same result.

From intuition, it is definitely feasible. And the truth is, yes. Here I record something about it.

I was thinking about if we can find out how these (4,12,12) vertex configurations distribute, it is easy to replace them by corresponding super-tiles, which requires only few information of cluster.

As for the connection between these substitution rule and TralityTree, maybe more likely there is a connection between TralityTree and H-supertile, which are both in a "triangle" shape. We will find out if there is a further connection.

Notice that the $H$ cluster is in 1-to-1 correspondence with reflected tiles only occurring at location $H_1$. The $A+$ edge of $H$ is (from what we've found) the strongest starting place for growing $H_7$ and $H_8$. Counting the two clusters separately, { $H_7$, $H_8$} are in a 2-to-1 correspondence with reflected hats (but the ratio of $H_7$ : $H_8$ is not $1:1$).

Do not be deluded by boundary shape, which is really just an accident of how well the rules have been chosen on edges. My first choice was not so nice, so I kept going through subsequent choices until arriving at something aesthetically pleasing.

I've repeated the code from the WFR site, with extra highlighting to show how two of the symmetric trivalent vertices are selected from the set of eight, and then used to project supertiles to cover the Cartesian space:

Your highlighted $(4,12,12)$ are seen in this image as green and yellow plus one extra gray tile on the outside of the $A+$ edge. Green always falls on an $H_7$ supertile, but in my convention, yellow does not. Yellow tiles are found on both $H_7$ and $H_8$ in an extended position outside of the central $H$ meta-tile.

From what I've heard, Craig made the choice to have both $H_7$ and $H_8$ with complete surrounds of the central tile and thus complete $H$ meta-tiles directly inlaid. This choice is inconsistent with the map from vertex figures, because it would result in overlap of the $H_2$ occurring in every $H_7$. The solution was to parallel-translate the $H_2$ in $H_7$ to the extended location, which gives (imo) a more intrinsically-motivated definition for replacement rules.

Back to my question above: If we suspend belief in the aesthetic choice of completing a surround for every reflected tile, and pursue the tree-motivated definitions more directly, does the resulting substitution system on two-dimensional tiles have any additional nice properties from being defined more naturally?

Yeah, the control points are important here. And I choose them by observation as well as attempts from H2&H1 to H7&H8, just to create these fractal bigger cluster. The main idea is, find some important points to place the next cluster, since the rotation angles are fixed (that is substitution).

More exactly, this is how my code works:

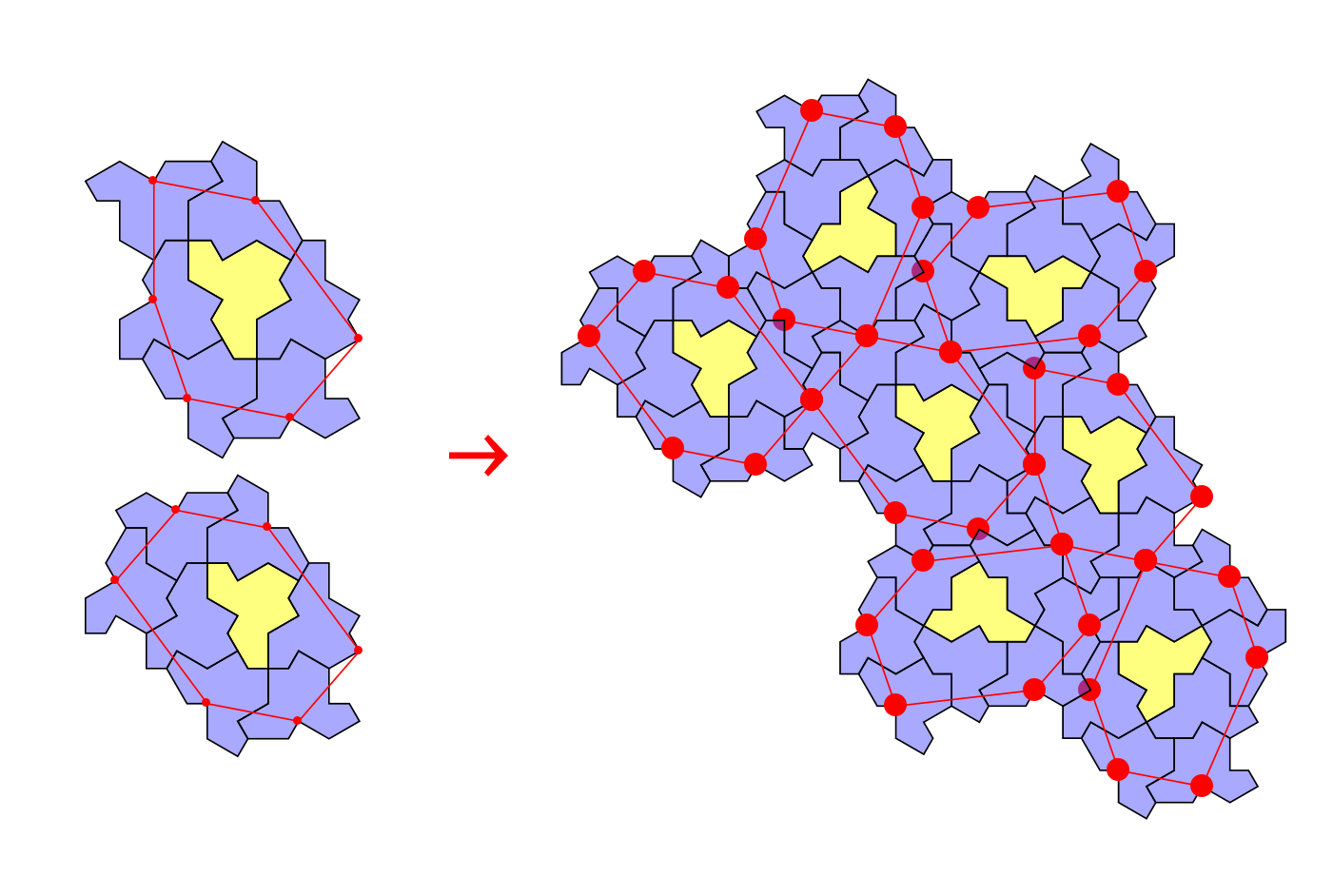
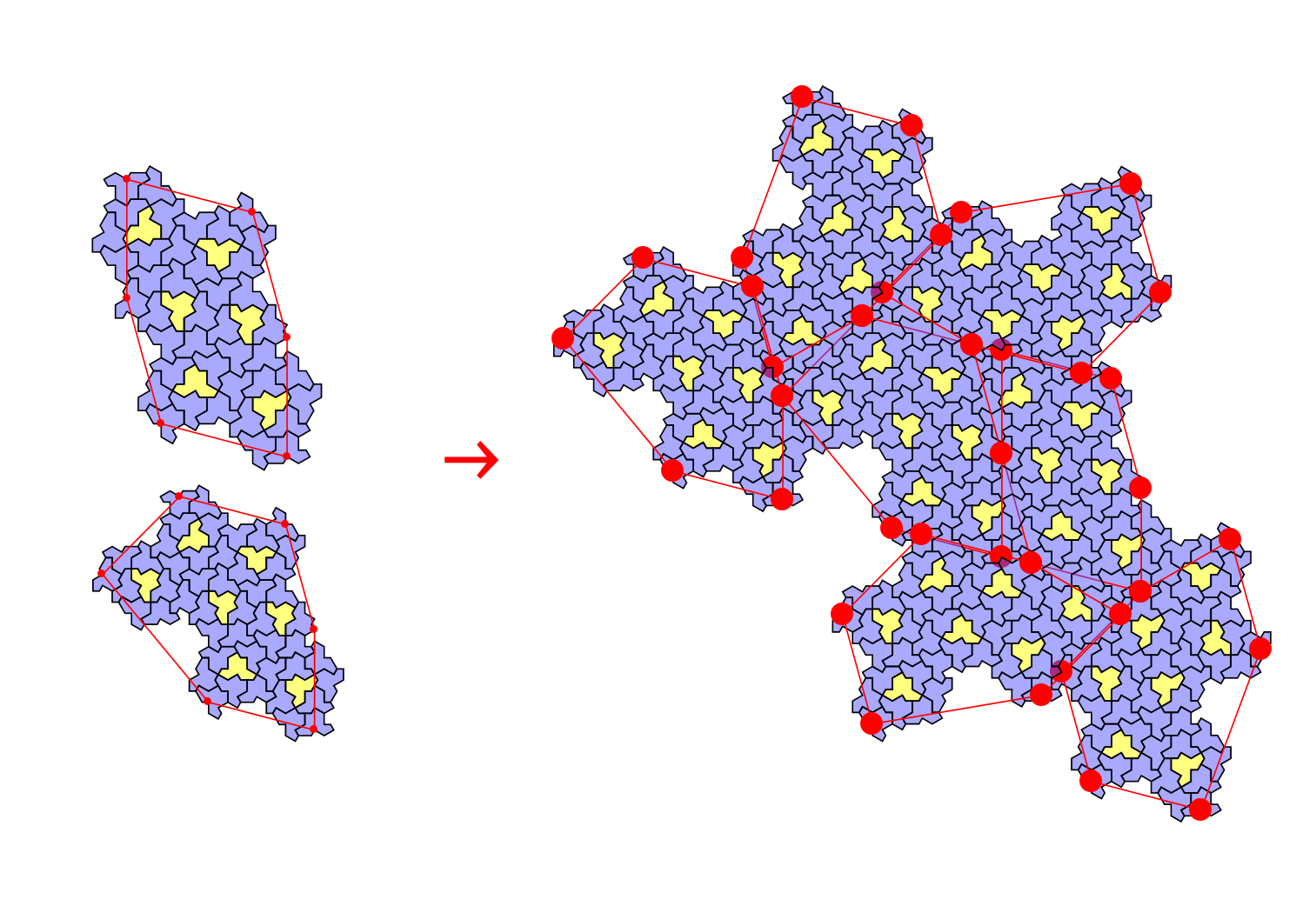
As you can see, I choose some important points where the clusters next connect to each other. By these points we can determine how to construct the next cluster.

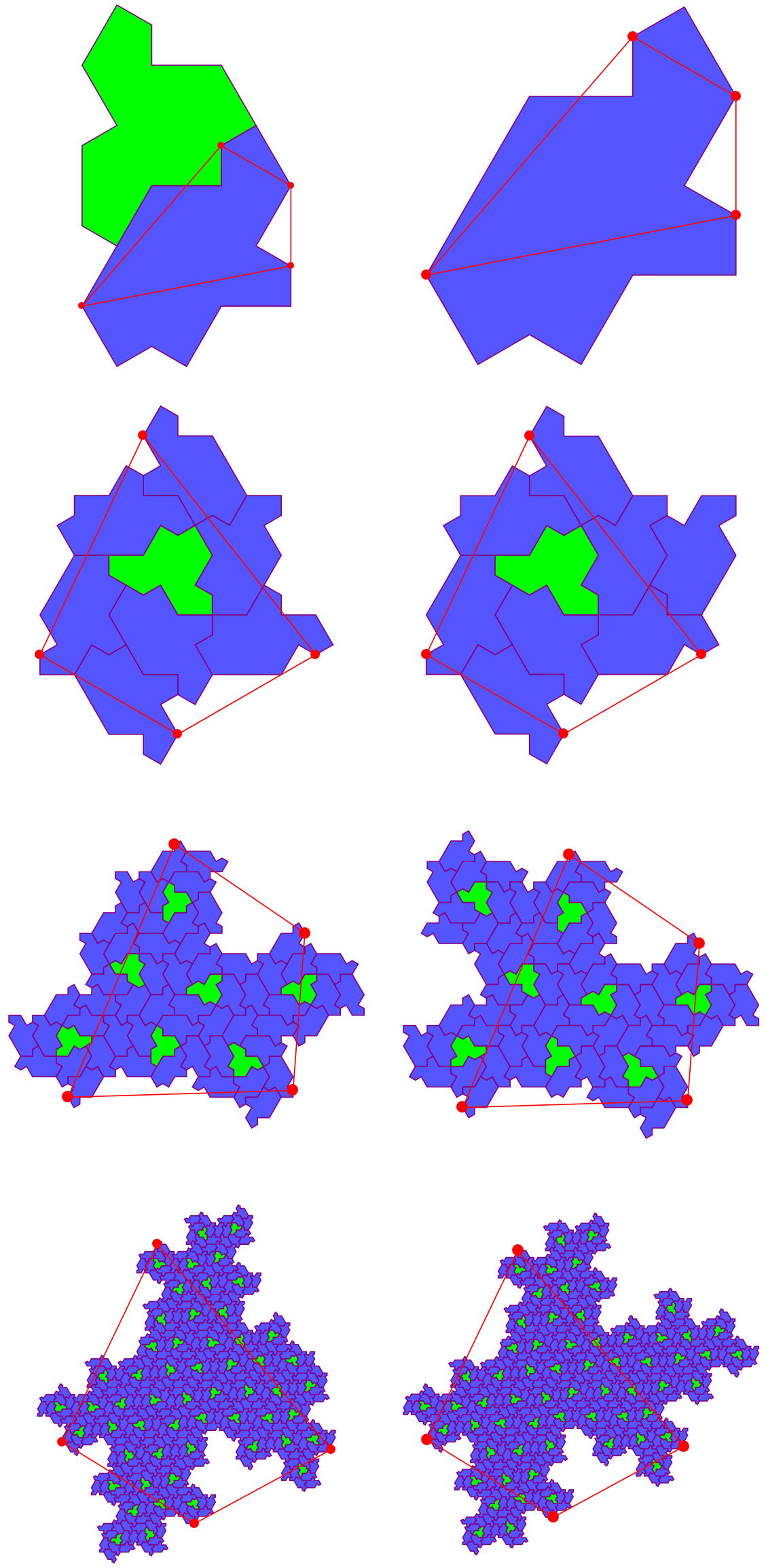
By the way, this "control points" or "key points " idea is similar as what author used to construct spectre cluster in this video, which results this kind of fractal structure:

Few hats and many turtles:

Few turtles and many hats:

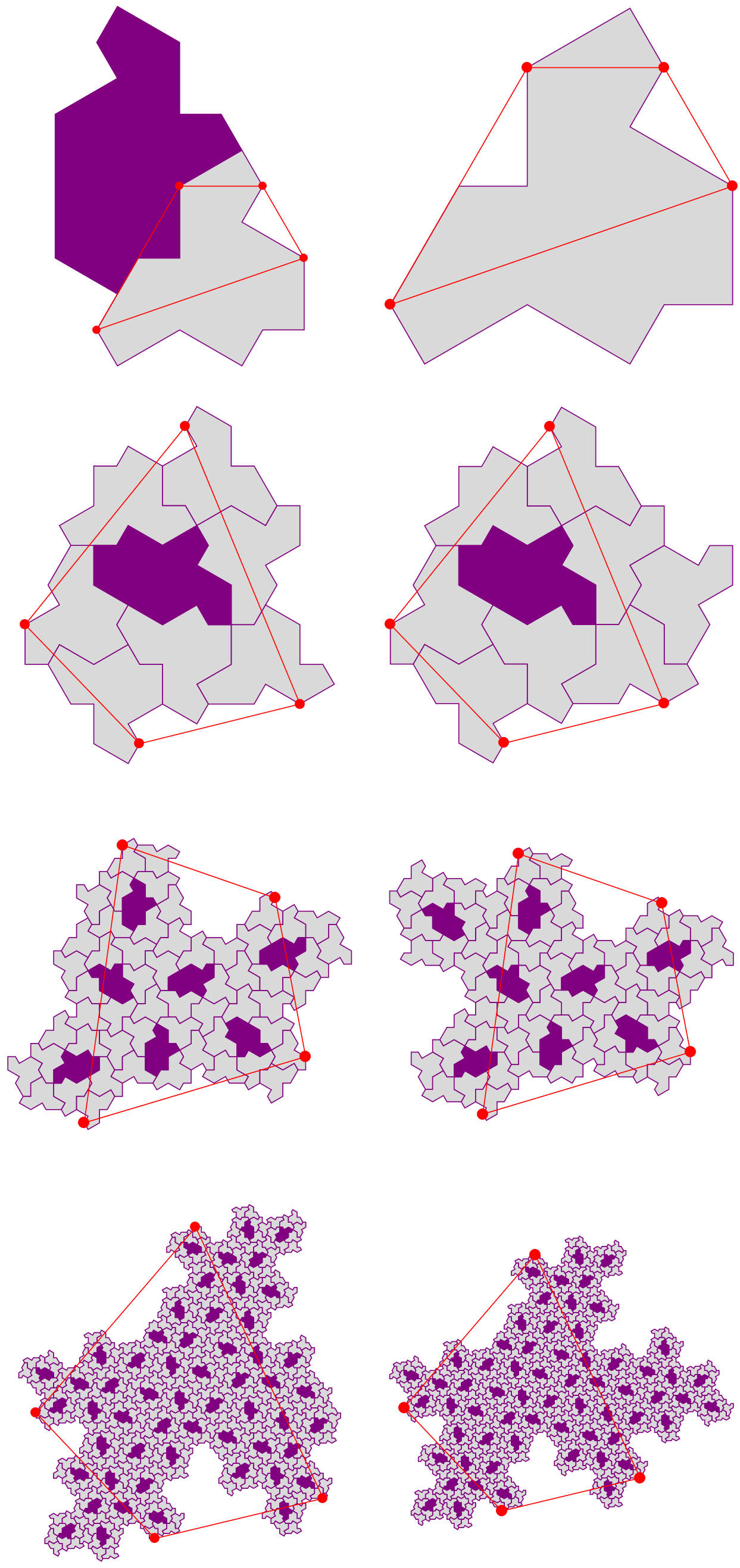
Only spectre:

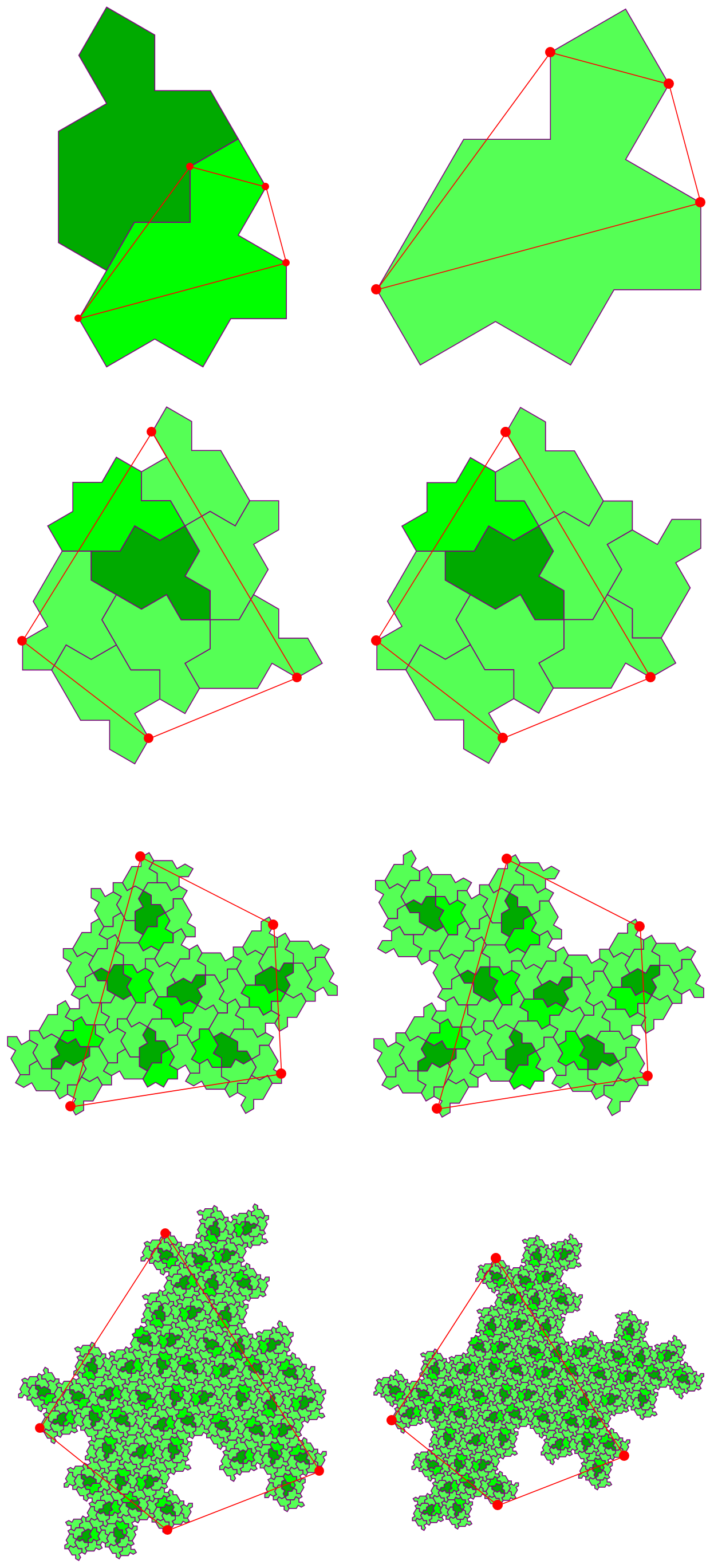
The figures above are what the author shows in the video. Inspired by that, I tried this idea on hat tiles to reproduce the process of this fractal substitution in the paper, which is this post. Then, I wanted to do the same thing on spectre tiles but failled, since the substitution rule of spectre in the original paper requires reflection, which is a little tricky. So, I reviewed that video and reproduce what author did. Then we have the figures above.

I think the definition of H7 and H8 is just for making sure their substitution rule shown in paper works. I agree with you about "for aesthetic reasons". The fractal stuff never disappoints people. And for HatTralitytree, I was about to study something about it but it turned out I need a enormous cluster to find out a pattern of these vertices. Since I find that one (4,12,12) configuration determines one H8 hat super-tile, plus 3 more tiles exactly, which seems like a connecting bridge between these super-clusters.

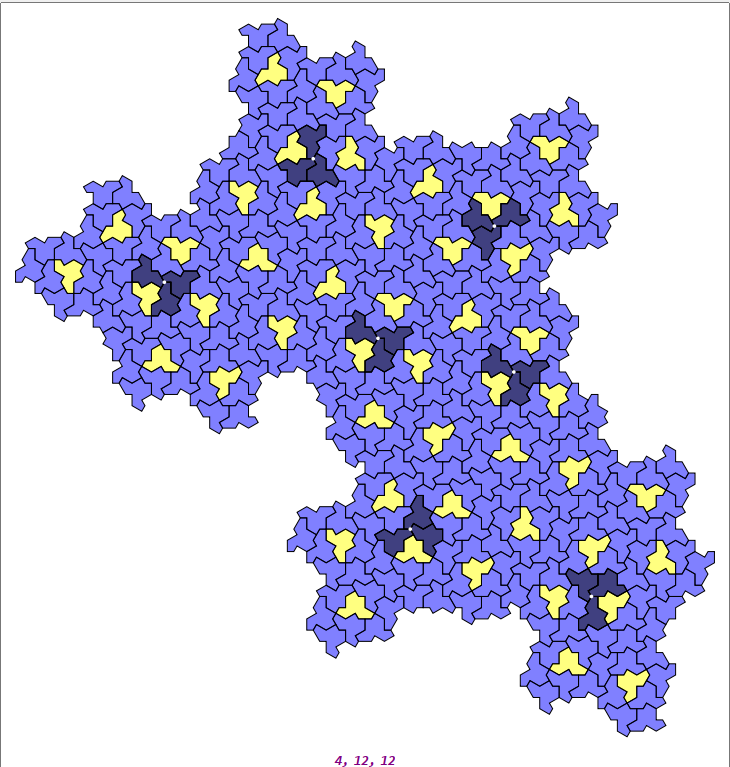
I was thinking about if we can find out how these (4,12,12) vertex configurations distribute, it is easy to replace them by corresponding super-tiles, which requires only few information of cluster.

As for the connection between these substitution rule and TralityTree, maybe more likely there is a connection between TralityTree and H-supertile, which are both in a "triangle" shape. We will find out if there is a further connection.

-- you have earned Featured Contributor Badge Your exceptional post has been selected for our editorial column Staff Picks http://wolfr.am/StaffPicks and Your Profile is now distinguished by a Featured Contributor Badge and is displayed on the Featured Contributor Board. Thank you!