Hi,

I am trying to solve 2D PDEs with NDSolveValue[] (Mathematica 10 windows & linux both), but I always get some errors with the derivative boundary conditions. For example:

uif = NDSolveValue[D[f[x, y], {x, 2}] + D[f[x, y], {y, 2}] == 1 && Derivative[1, 0][f][1, y] == 1 && f[0, y] == 1, f, {x, 0, 1}, {y, 0, 1}]

solves a simple Poisson equation on a square (0,1)x(0,1), with \partial f / \partial x =1 on x=1. However, the solution uif always gives wrong answer:

Plot[Derivative[1, 0][uif][x, 0.5], {x, 0, 1}]

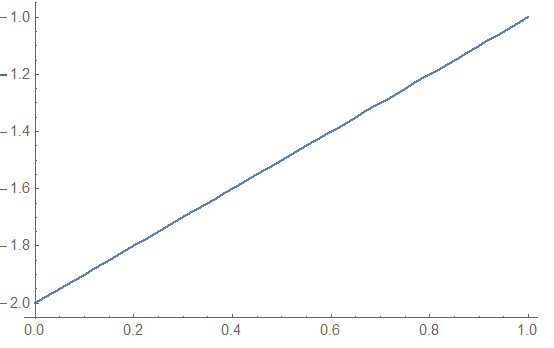
So the derivative of the solution at x=1 is the negative of the condition specified.

If I specify Derivative[1, 0][f][0, y] == 1, (same condition at x=0), the answer would be correct. Same thing would happen for all my test PDEs.

Is Mathematica 10 assuming that the boundary condition specified is affected by the normal vector on the boundary? Or how should I specify the boundary conditions appropriately?

Thank you,