Hi,
what about this:
t = Flatten[Table[{x, y, x^2 + y^2}, {x, -1, 1, .1}, {y, -1, 1, .1}], 1];
ft = Interpolation[t];
Just test that it works:
Plot3D[ft[x, y], {x, -1, 1}, {y, -1, 1}]
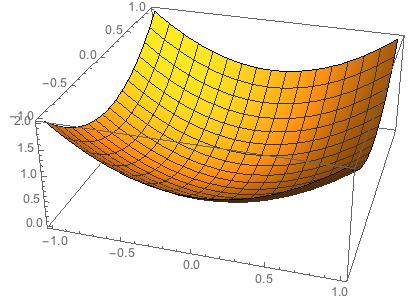
Ok. Now plot the derivative
Plot[D[ft[x, .5], x] /. x -> z, {z, -1, 1}]
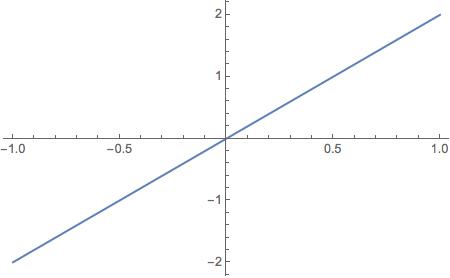
So
D[ft[x, .5], x] /. x -> 0.25
should do the trick. Similarly,
\!\(\*SubscriptBox[\(\[Del]\), \({x, y}\)]\(ft[x, y]\)\) /. {x -> 0.25, y -> 0.5}
looks alright. We can also define a new function
gradf[u_, v_] := \!\(\*SubscriptBox[\(\[Del]\), \({x, y}\)]\(ft[x, y]\)\) /. {x -> u, y -> v };
and then use
gradf[0.25, 0.5]
but I am sure that there is a more elegant way.
Cheers,
Marco