Message Boards Message Boards

0
|
2405 Views
|
6 Replies
|
1 Total Likes
View groups...
Share
Share this post:

3D Plotting of Time Dilation near Black holes

Estelle Asmodelle
Posted 1 year ago

Hi there,

I have some basic code for plotting the gravitional time dilation as one moves closer to the event horizon of a black hole of a given mass. See code:

ClearAll["Global`*"]'; tp = 1; G = 
 6.67408*10^(-11); M = (6.5*10^9)*(1.989*10^30); c = 
 2.99*10^8; rs = (2*G*
    M)/(c^2); Print[]; Print["    Black hole mass:", M, "kg", "    \
Schhwarzchild radius:", rs, "m"]; Print[]; Plot[
 tp*Sqrt[1 - (rs/r)], {r, 0, 2*10^14}, AxesLabel -> {" ", "Time (s)"},
  AxesLabel -> {Style["  (m)", Bold, 26], 
   Style["Time (s)", Bold, 16]}, LabelStyle -> Directive[Black, 16], 
 AxesOrigin -> {0, 0}, GridLines -> {{rs}, {}}, 
 GridLinesStyle -> {Directive[{Dashed, Thick}, Red], 
   Directive[Thick, Red]}, ColorFunction -> "NeonColors"]

I want to create a 3D plot for different masses of black holes ranging from the one given in the code to one a thousand times more massive, with a 3D sheet. I am not great at this, and while my basic code works fine, when I go to do a 3D plot, nothing seems to work.

Attachment

Attachments:
Capture3.JPG
POSTED BY: Estelle Asmodelle
6 Replies
Sort By:

Here are just some thoughts: You can do the plot with logarithmic scaling like so:

Plot3D[tp*Sqrt[1 - ((2*G*M)/r)], {r, 0, 2*10^14}, {M, 
  1, (6.5*10^9)*(1.989*10^90)}, AxesLabel -> {" ", "Time (s)"}, 
 AxesLabel -> {Style["  (m)", Bold, 26], Style["Time (s)", Bold, 16]},
  LabelStyle -> Directive[Black, 16], AxesOrigin -> {0, 0}, 
 Filling -> {1 -> Top}, PlotRange -> All, 
 ScalingFunctions -> {"Log", "Log"}]

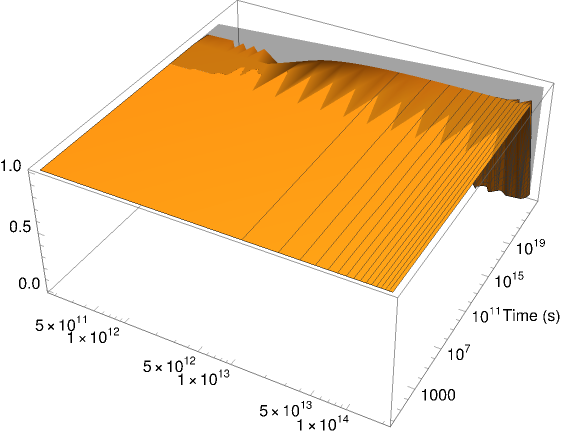
enter image description here

Or instead of going to very high values with the arguments you simply go straight to infinity - MMA can actually do those plots!

Plot3D[tp*Sqrt[1 - ((2*G*M)/r)], {r, 0, Infinity}, {M, 1, Infinity}, 
 AxesLabel -> {" ", "Time (s)"}, 
 AxesLabel -> {Style["  (m)", Bold, 26], Style["Time (s)", Bold, 16]},
  LabelStyle -> Directive[Black, 16], AxesOrigin -> {0, 0}, 
 Filling -> {1 -> Top}, PlotRange -> All]

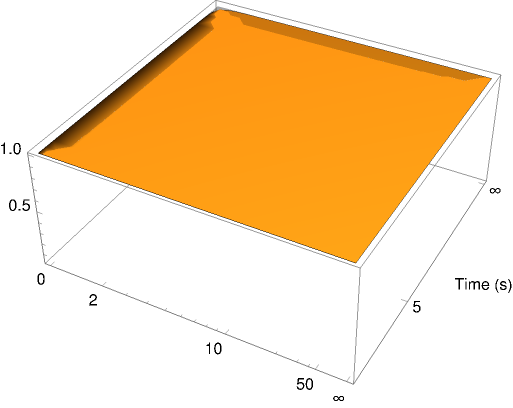
enter image description here

Maybe that might be on option when dealing with those very big numbers anyway.
POSTED BY: Henrik Schachner

Thanks, you got similar results to my attempt but something is wrong with the plots.
POSTED BY: Estelle Asmodelle

Try expressing your input in Sun masses, or something like that.
POSTED BY: Gianluca Gorni

I think I tried geometrized units but I will give it another go.

Thanks.
POSTED BY: Estelle Asmodelle

Very curious. Plots such as this

Plot3D[1 + (m/r), {r, 0, 10^11}, {m, 0, 10}]

give an empty box. The problem may be related to the large number 10^11. Try rescaling your problem so as to use smaller numbers.
POSTED BY: Gianluca Gorni

Indeed, hence the post. I also get an empty box.

ClearAll["Global`*"]'; tp = 1; G = 
 6.67408*10^(-11); M = (6.5*10^9)*(1.989*10^30); c = 
 2.99*10^8; Print[]; Print["    Black hole mass:", M, "kg", "    \
Schhwarzchild radius:", rs, "m"]; Print[]; Plot3D[
 tp*Sqrt[1 - ((2*G*M)/r)], {r, 0, 2*10^14}, {M, 
  1, (6.5*10^9)*(1.989*10^90)}, AxesLabel -> {" ", "Time (s)"}, 
 AxesLabel -> {Style["  (m)", Bold, 26], Style["Time (s)", Bold, 16]},
  LabelStyle -> Directive[Black, 16], AxesOrigin -> {0, 0}, 
 Filling -> {1 -> Top}, PlotRange -> 2]

The numbers have to stay the same as otherwise the plot means nothing. I even tried Log plot with no luck.
POSTED BY: Estelle Asmodelle
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract