Hi Alexander,
I don't think that ImageFeatureTrack will work here. It is quite simple to visualise the differences between the two images:
ImageSubtract[images[[1]], images[[2]]] // ImageAdjust
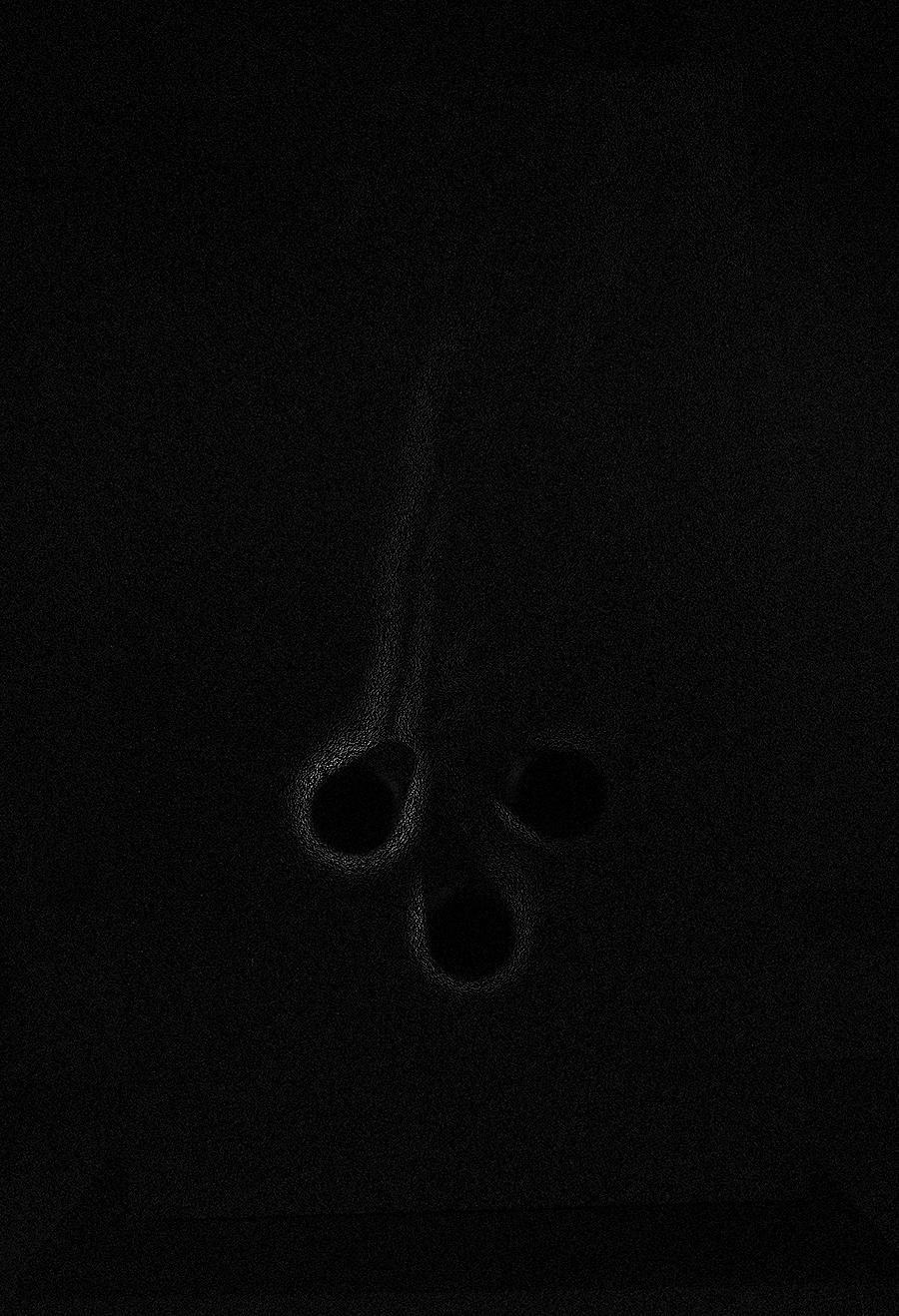
You can also colorise that:
Colorize[ImageAdjust[ImageSubtract[images[[1]], images[[2]]]], ColorFunction -> "ThermometerColors"]
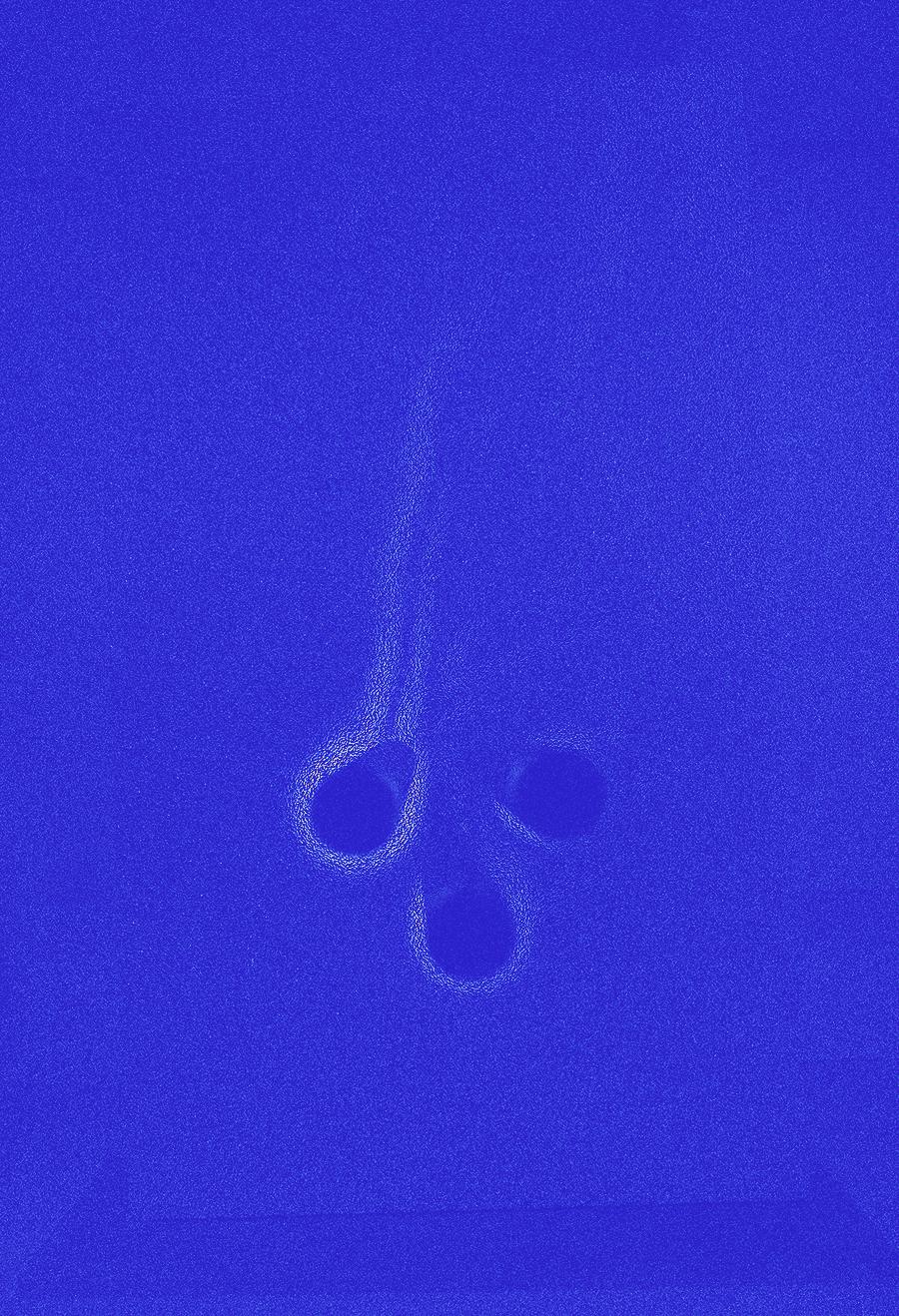
You can then zoom in onto one of the pins
img=ImageTrim[Colorize[ImageAdjust[ImageSubtract[images[[1]], images[[2]]]], ColorFunction -> "ThermometerColors"], {{270., 420.}, {460., 630.}}]

You can make the structures a bit clearer with
MorphologicalBinarize[img] // Colorize
I particularly like this one:
MorphologicalComponents[Binarize[img]] // Colorize
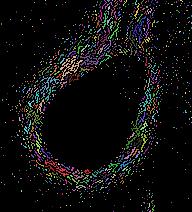
I know that this is not what you want, but as I said I think that ImageFeatureTrack will not work well.
If you draw the Key Points you get
Show[Graphics[{Green, Disk[#, 5]} & /@ ImageKeypoints[images[[1]]]],
Graphics[{Red, Disk[#, 5]} & /@ ImageKeypoints[images[[2]]]]]

the thing is that even the number of key points does not match up. 7180 in one and 7186 in the other. there is no reason to assume that they "match up". In fact if you draw lines between them that looks horrible:
Graphics[Line /@ Transpose[{ImageKeypoints[images[[1]]][[1 ;; 7180]], ImageKeypoints[images[[2]]][[1 ;; 7180]]}]]

This command does something similar to what you want; it produces still error messages, because some points are missing, but never mind.
Show[images[[1]], Graphics[{Green, Disk[#, 5]} & /@ features[[1]]], Graphics[{Red, Disk[#, 5]} & /@ features[[2]]], Graphics[{Thick, Line[#]} & /@
Transpose[{features[[1]], features[[2]]}]]]

I can fix the missing problem if you want.
Cheers,
Marco