Oh do you mean defining the metric tensor g for a given spacetime..for example..the Schwarzchild metric in spherical coordinates..then we can tag these coordinates with variable values so that we can define them. I suppose there are three primary points I want to make like let's say you wanna define things like energy density, pressure, 4-velocity. Then suppose there's a perfect fluid and you define the Stress-Energy-Momentum tensor for it. Where Rho is the constant energy density, p0 is the constant pressure, and the ...stress energy tensor for a perfect fluid.
metric = {
{-(1 - 2 M/r), 0, 0, 0},
{0, 1/(1 - 2 M/r), 0, 0},
{0, 0, r^2, 0},
{0, 0, 0, r^2 Sin[\[Theta]]^2}
};
coords = {t, r, \[Theta], \[Phi]};
\[Rho] = \[Rho]0;
p = p0;
u = {1, 0, 0, 0};
stressEnergyTensor = (p + \[Rho]) Outer[Times, u, u] + p metric;
stressEnergyTensor // MatrixForm

Do we need the xAct system..that could be what kind of command ..maybe the order of operations does "matter". How do you perform efficient and organized calculations involving tensors "outside" of Mathematica? How do you run just the commands to compute Stress-Energy-Momentum tensor in General Relativity?
dim = 4;
coords = {t, r, \[Theta], \[Phi]};
metric =
DiagonalMatrix[{-1/(1 - 2 M/r), 1/(1 - 2 M/r), r^2,
r^2 Sin[\[Theta]]^2}];
inverseMetric = Simplify[Inverse[metric]];
Print["Metric Tensor:", metric];
Print["Inverse Metric Tensor:", inverseMetric];
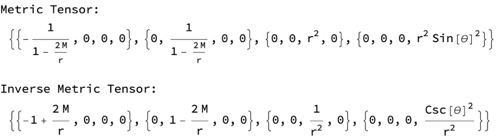
You could do some multi-threaded Parallelize distribution of listable operations over multiple kernels.