I have a model written with the MultiBody Modelica Library, and I'm trying to symbolically calculate a linear approximation in Mathematica using SystemModelLinearize, however, the procedure freezes at the stage of "Preparing variables":  I wonder if it's possible to simplify the model such that the symbolic linearization can proceed.
I wonder if it's possible to simplify the model such that the symbolic linearization can proceed.
I assume it could be challenging to identify the exact the problem, but I have a suspect model. Changes in this model led to the freezing of the linerization procedure. Here is a screenshot of the FlexureLowerEnergy model:
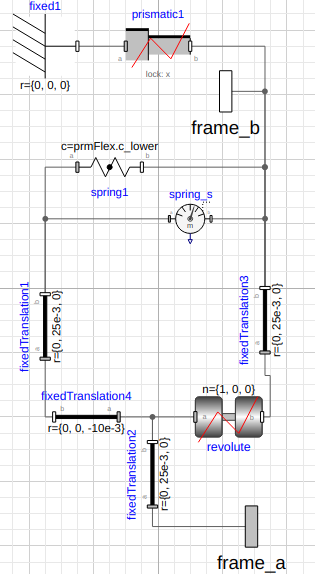
The aim of some components is to set a boundary condition. The frame frame_b of fixedTranslation3 must remain parallel to the ground frame, i.e., it can translate in Z and Y but not rotate. At the outside, frame frame_a is connected to the bottom of a pendulum (blue and pink in the figure below) that oscillates, and frame_b is connected to a Body object: 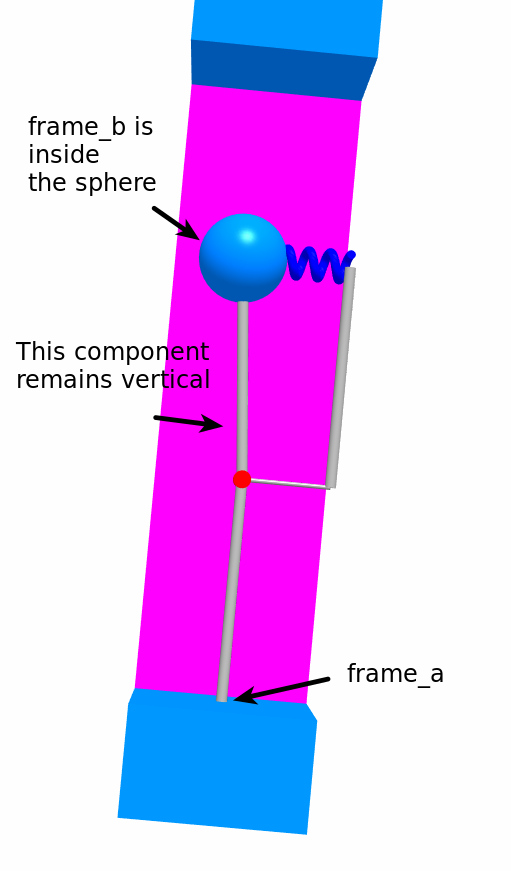
The boundary condition is set by the prismatic constraint prismatic1 and the revolute planar loop constraint revolute. Thus, the component fixedTranslation3 remains vertical as the pendulum oscillates. The boundary condition holds without the spring, but the spring is necessary to calculate potential energy and other relevant physical quantities.
I suspect the symbolic linearization procedure is not able to cope with the prismatic constraint. Is there a more suitable way to set this boundary condition?
Please note that the method suggested in this post does not work for symbolic linearization because it uses an angular position source which uses a numerical low pass-filter. Even when the linearization is numerical, this low pass filter produces problems in transfer functions at high frequencies.
I attach the System Modeler file with the model and a Mathematica file. I'm using System Modeler 13.2.0 and Mathematica 13.2.
Any help will be highly appreciated.
Regards,
Fabián
 Attachments:
Attachments: