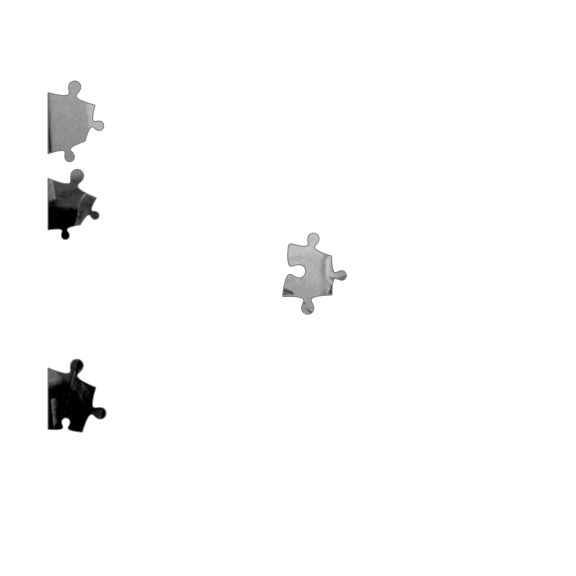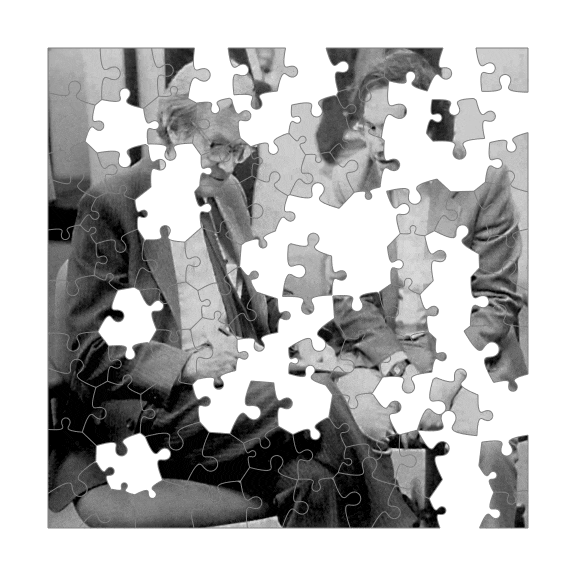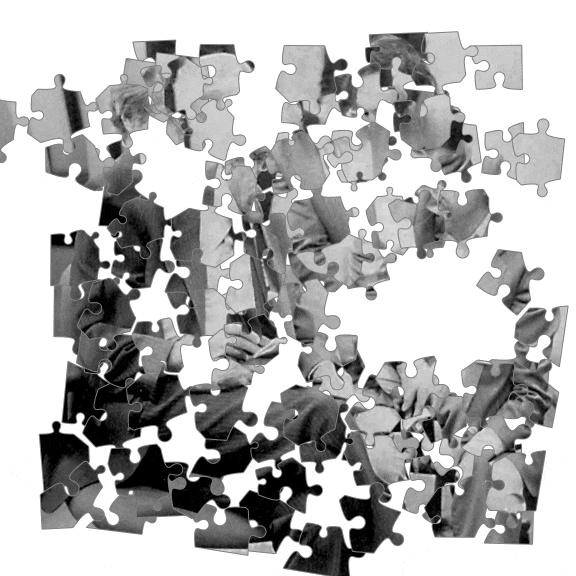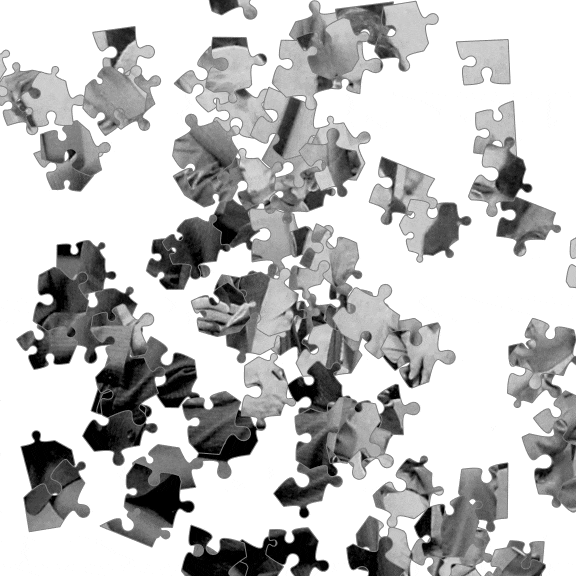
Dear all, from the resemblance of a Voronoi mesh to a jigsaw puzzle I came to the idea for the following little program I want to share. The essential function is
(* in: points p1, p2;
out: BSplineCurve = jigsaw side if distance > minLength; *)
jigsawSide[minLength_][pts : {p1_, p2_}] := Module[{m, u, o, vx, vy, n, dist, r, c, angle0, cPts},
dist = EuclideanDistance @@ pts;
If[dist < minLength, Return[Line[pts]]];
(* avoid borders: *)
If[Times @@ (p2 - p1) == 0, Return[Line[pts]]];
m = Mean[pts];
{u, o} = SortBy[pts, Last]; (* lower/upper point *)
{vx, vy} = o - u;
n = {vy, -vx}; (* normal vector *)
r = .15 dist; (* radius *)
c = m + n/4.; (* center *)
angle0 = Sign[Last[n]] VectorAngle[{1, 0}, n];
(* points on circle: *)
cPts = c + r {Cos[angle0 + #], Sin[angle0 + #]} & /@ (60 \[Degree] {-2, -1, 0, 1, 2});
Return[BSplineCurve[{u, m, Sequence @@ cPts, m, o}]]
]
which connects two points with a BSplineCurve having the typical elementary shape of a jigsaw puzzle. If the distance is too short then the connection becomes a straight line. The same happens if the points share the same x- or y-coordinate to exclude the jigsaws borders. Here is a simple test of the function:
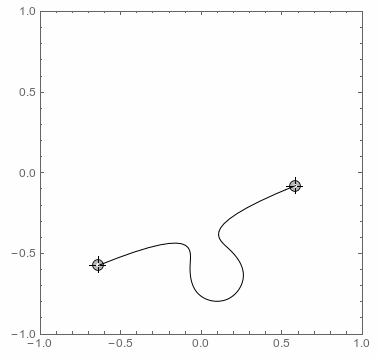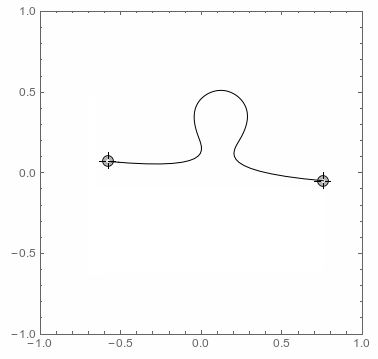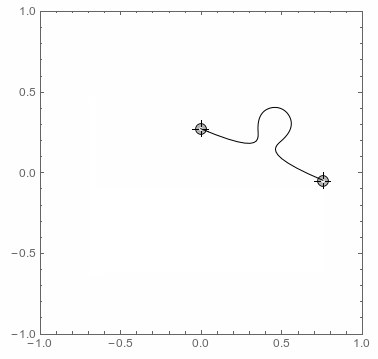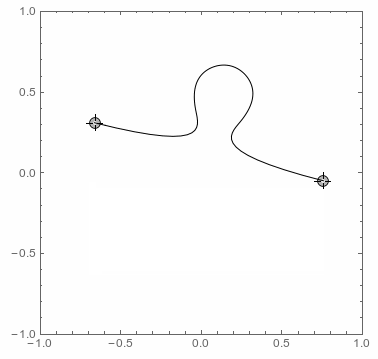
Anything else is straightforward:
- start with "randomized" lattice points;
- from these a Voronoi mesh is created;
- extract its polygons;
- convert the polygon sides into the new (puzzle) shape;
- build new polygons out of these sides;
- apply a texture.
The result is a bunch of jigsaw pieces one can play with:

I was impressed by the consistent behavior of Texture. The whole (short) code is attached.
Best regards -- Henrik
 Attachments:
Attachments: