Thanks for your consideration.
I'm working to create a solution of an Ornstein-Uhlenbeck process with a force that takes mass towards the centre of a Simplex. I'm assuming absorbing boundaries.
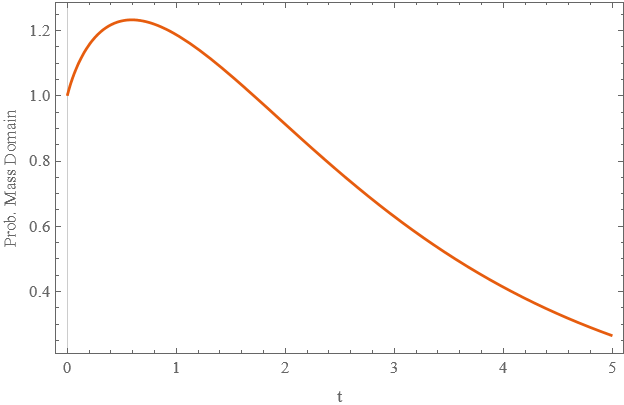
The Mathematica code below quickly provides a solution. However, the probability mass within the domain grows significantly early, but it should only ever diminish, due to mass being absorbed.
I don't think the error lies in my formulation of the forward Kolmogorov (Fokker-Plank) equation.
If it doesn't lie there, I suppose it could lie in the numerical approximation, with errors growing? I greatly appreciate any insight into this problem.
ClearAll["Global`*"]
\[Eta] = 5.; (*side length*)
xopt = {\[Eta]/2, \[Eta]/(2 Sqrt[3])}; (*centroid*)
\[Kappa] = .75; (*rate of reversion to centroid,diffusion constant=1*)
Tmax = 5.; (*length of time*)
\[CapitalOmega] =
Polygon[Rationalize[{{0, 0}, {\[Eta],
0}, {\[Eta]/2, (\[Eta] Sqrt[3])/2}},
0]]; (*domain is equilateral triangle*)
bC = Rationalize[DirichletCondition[P[x1, x2, t] == 0, True],
0]; (*absobing boundary condition*)
iC = Rationalize[
P[x1, x2, 0] ==
Piecewise[{{1/((Sqrt[3] \[Eta]^2)/4),
RegionMember[\[CapitalOmega], {x1, x2}]}}, 0],
0]; (*uniform initial condition*)
(*forward Kolmogorov equation*)
fwrdKol =
Rationalize[
D[P[x1, x2, t],
t] == -D[\[Kappa] (xopt[[1]] - x1)*P[x1, x2, t], {x1, 1}] -
D[\[Kappa] (xopt[[2]] - x2)*P[x1, x2, t], {x2, 1}] +
1/2 D[P[x1, x2, t], {x1, 2}] + 1/2 D[P[x1, x2, t], {x2, 2}], 0];
(*numerical solution*)
Psol = NDSolveValue[{fwrdKol, iC, bC},
P, {x1, x2} \[Element] \[CapitalOmega], {t, 0, Tmax}];
(*visualise solution at a t=Tmax/2*)
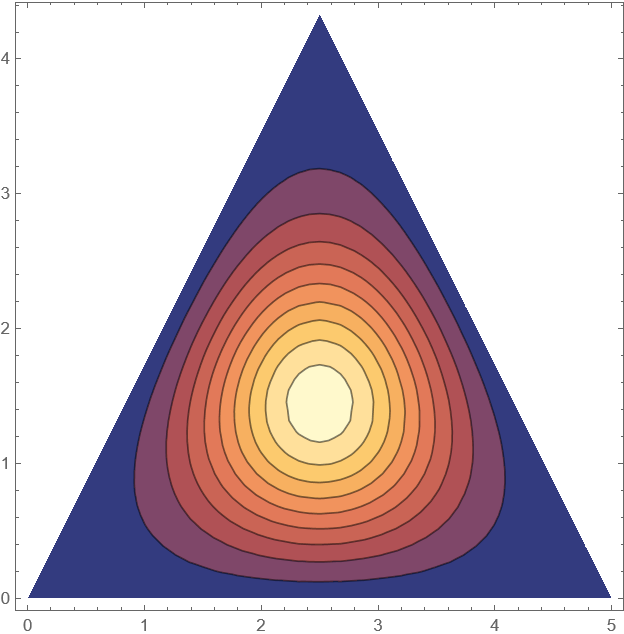
ContourPlot[Psol[x1, x2, Tmax/2], {x1, x2} \[Element] \[CapitalOmega]]
(*probability mass within domain*)
domP[t_] :=
NIntegrate[
Rationalize[Psol[x1, x2, t],
0], {x1, x2} \[Element] \[CapitalOmega], AccuracyGoal -> 4]
(*visualise*)
Plot[domP[t], {t, 0, 5}, PlotTheme -> "Scientific", PlotRange -> All,
FrameLabel -> {"t", "Prob. Mass Domain"}]