Hi
I want to find the coefficients a & b for the equation (a*V^3+b = Ws). I have a hand-drawn graph, which is an empirically-derived polar of sink rate vs speed for a sailplane 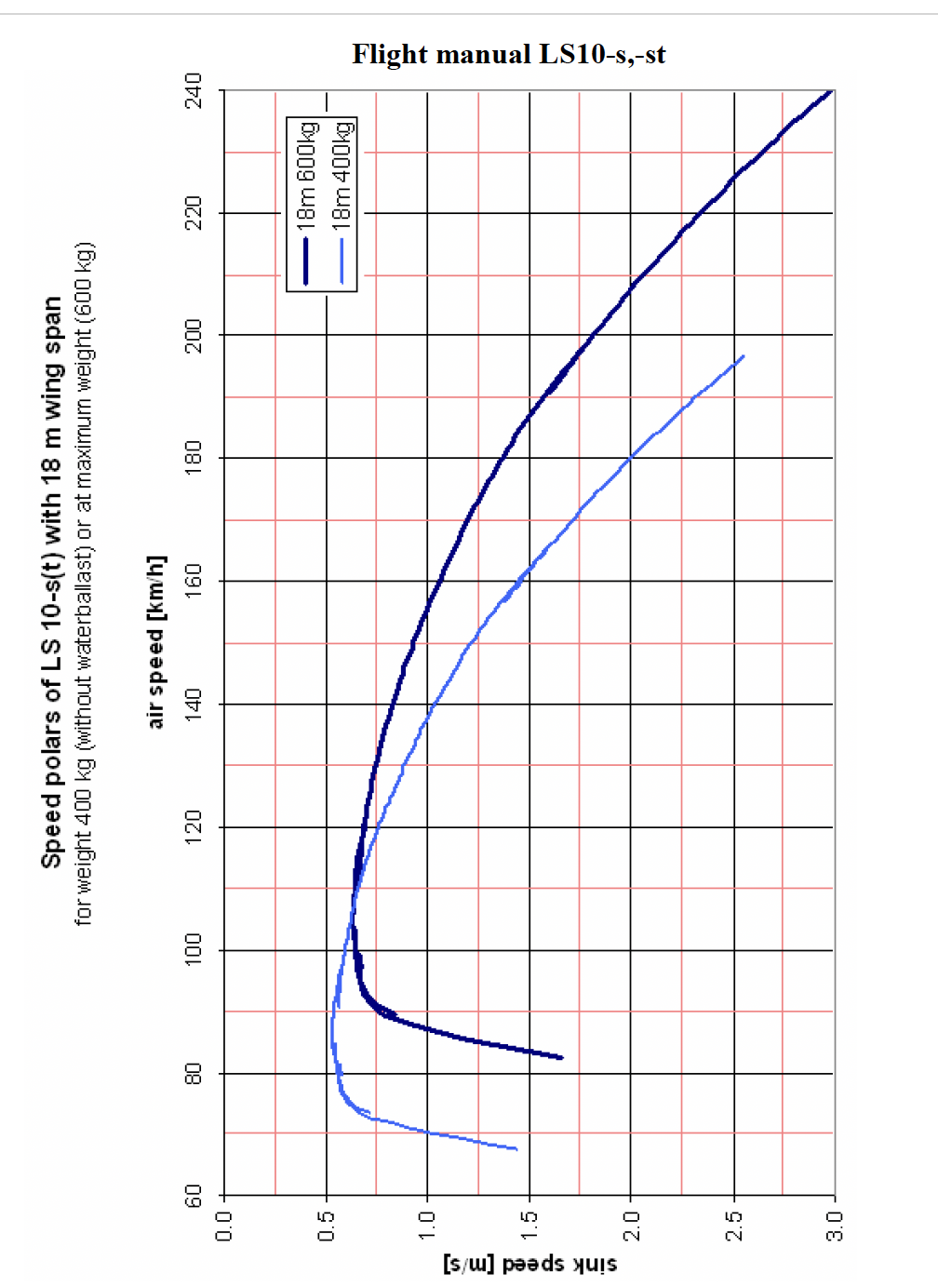
The graph can also be described by the quadratic (aV^2+bV+c = Ws), and I am able to derive these coefficients, using formulae given in Reichmann (p105) with 3 sets of coordinates read from the physical graph. This gives a pretty good fit.
However, it's reported that the cubic form a*V^3 + b is more accurate. I don't know, but would like to try and derive the a & b coefficients. However, I don't have handy algebraic solutions. I have tried iterating over a range of possible solutions in Python but, at 4+ billion loops, it's a rather clumsy process.
Can anyone suggest a Wolfram function that would factorize or expand this cubic and thus simplify the muscling required, or alternatively know of an algebraic method?
 Attachments:
Attachments: