Hello, right now I'm trying to replicate an optimization algorithm from a research paper, but I'm getting different results. In the paper, when the frequency parameter n is set to 20, the resulting value of T should be 1.67 and the profit TP should be 421.14. However, when I set n to 20 in Mathematica, I get T = 0.09 and TP = -1743. I tried to recheck the equation I wrote in Mathematica and recheck the parameter value as well but the result still did not match. I've been working on this for a while and I'm starting to run out of ideas. Here is the algorithm and the equation I try to follow : 
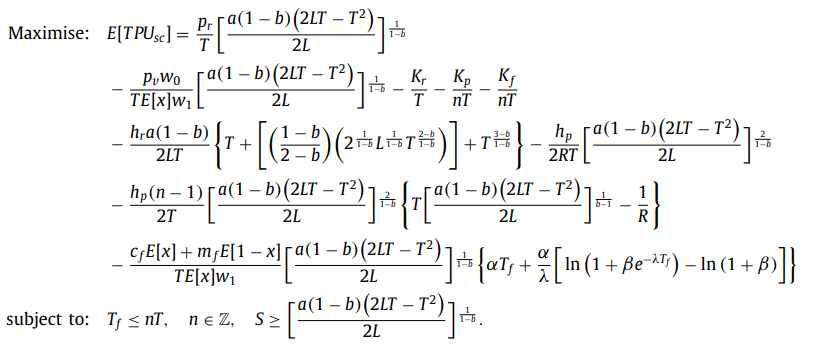 And also, here is the numerical example and the result that was written in the paper :
And also, here is the numerical example and the result that was written in the paper : 
 Here is the code I wrote in mathematica :
Here is the code I wrote in mathematica :
Clear["Global`*"]
L = 4;
w = 0.064;
ww = 2;
R = 250;
Kf = 750;
cf = 0.1;
m = 0.2;
Kp = 500;
hp = 0.05;
Kd = 100;
h = 0.1;
g = 6.87;
q = 0.12;
a = 80;
b = 0.2;
pv = 1;
pf = 2;
pr = 5;
z = 120;
n = 20;
x = 0.9;
s = 0.2;
Tf = - (Log[1/z (g/ww - 1)]/q);
F[d_] = pr/d ((a (1 - b) (2 L d - d^2))/(2 L))^(1/(1 - b)) - (pv w)/(
d x ww) ((a (1 - b) (2 L d - d^2))/(2 L))^(1/(1 - b)) - Kd/d -
Kp/(n d) - Kf/(
n d) - (h a (1 - b))/(
2 L d) (d + (((1 - b)/(
2 - b)) (2^(1/(1 - b)) L^(1/(1 - b)) d^((2 - b)/(
1 - b))) + d^((3 - b)/(1 - b)))) -
hp/(2 R d) ((a (1 - b) (2 L d - d^2))/(2 L))^(2/(1 - b)) - (
hp (n - 1))/(2 d) ((a (1 - b) (2 L d - d^2))/(2 L))^(2/(
1 - b)) (d ((a (1 - b) (2 L d - d^2))/(2 L))^(1/(1 - b)) - 1/
R) - (cf x + m s)/(d x ww) ((a (1 - b) (2 L d - d^2))/(2 L))^(
1/(1 - b)) (g Tf + g/q (Log[1 + z E^(-q Tf)] - Log[1 + z]));
FindMaximum[{Re@F[d], d > 0}, d]
Plot[F[d], {d, 0, 10}]
Note : I symbolize T as d and TP[T] as F[d] in Mathematica.
Does anyone have any insights into why this might be happening? Is there a step I might have missed?
 Attachments:
Attachments: