Knowledge of the data generation process is essential to get a good fit AND the "confidence" to trust predictions. You've mentioned limited resolution resulting in a "rolloff effect". That should be included in any modeling.

Maybe those issues result in departures from a square wave. So here is another parameterization of a trapezoidal wave. One feature is that one of the parameters (delta) is a measure of departure from a square wave. A delta value of zero results in a square wave. Below is a crude figure showing the parameterization for a single wave:

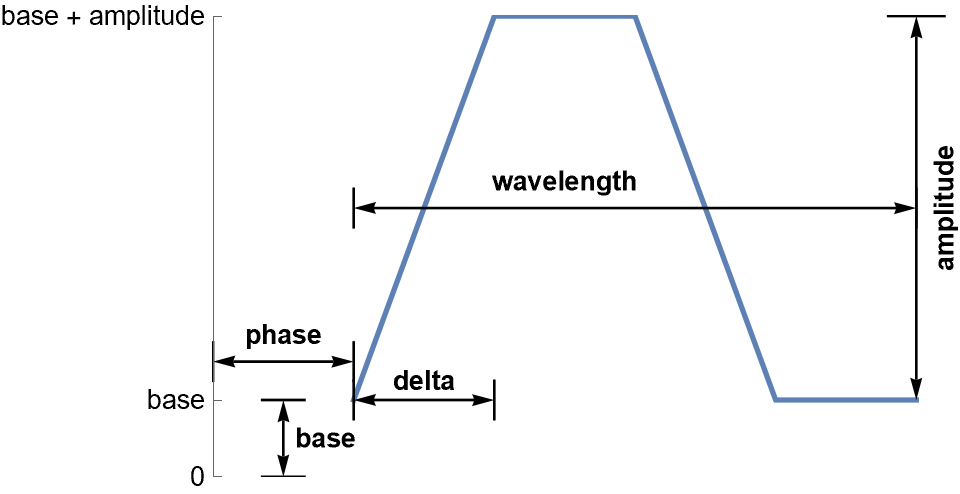
(* Trapezoidal wave function *)
f[x_?NumericQ, wavelength_?NumericQ, amplitude_?NumericQ, 
  phase_?NumericQ, base_?NumericQ, delta_?NumericQ] := Module[{s, y},
  s = Mod[x - phase, wavelength];
  If[s <= delta, y = base + amplitude s/delta,
   If[delta < s <= wavelength/2, y = base + amplitude,
    If[wavelength/2 < s <= wavelength/2 + delta, 
     y = base + amplitude (1 - (s - wavelength/2)/delta),
     y = base]]];
  y
  ]

data = {{-6.25, 0.00219649}, {-5.75, 0.0291773}, {-5.25, 0.0428364}, {-4.75, 0.0418075},
   {-4.25, 0.0390189}, {-3.75, 0.0142977}, {-3.25, 0.000728449}, {-2.75, 0.000577218},
   {-2.25, 0.00314383}, {-1.75, 0.0275447}, {-1.25, 0.0428128}, {-0.75, 0.0433703},
   {-0.25, 0.0433703}, {0.25, 0.0403935}, {0.75, 0.0160277}, {1.25, 0.000686316},
   {1.75, 0.00036222}, {2.25, 0.00288114}, {2.75, 0.0256044}, {3.25, 0.0416728},
   {3.75, 0.0429419}, {4.25, 0.0396677}, {4.75, 0.0162309}};

nlm = NonlinearModelFit[data, f[x, wavelength, amplitude, phase, base, delta],
   {{wavelength, 4}, {amplitude, 0.04}, {phase, 2}, {base, 0}, {delta, 0.5}}, x];

Show[ListPlot[data], Plot[nlm[x], {x, Min[data[[All, 1]]], Max[data[[All, 1]]]}]]

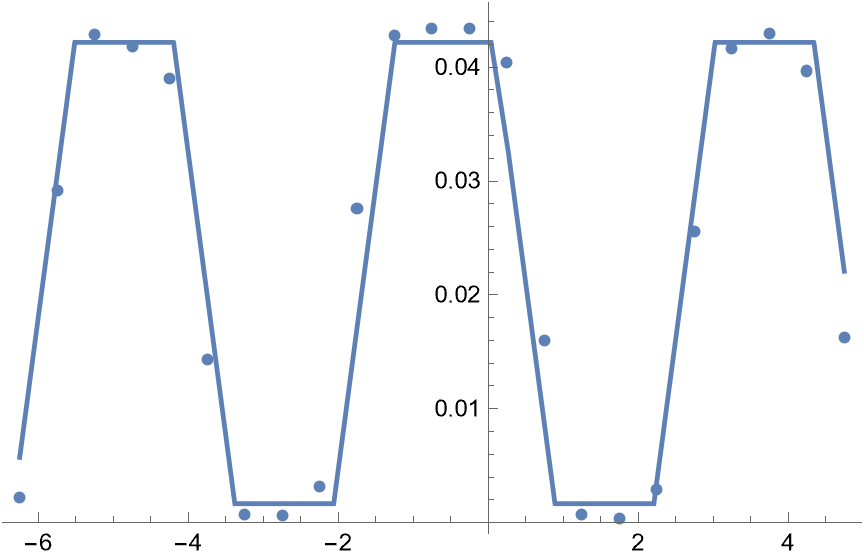
nlm["ParameterTable"]

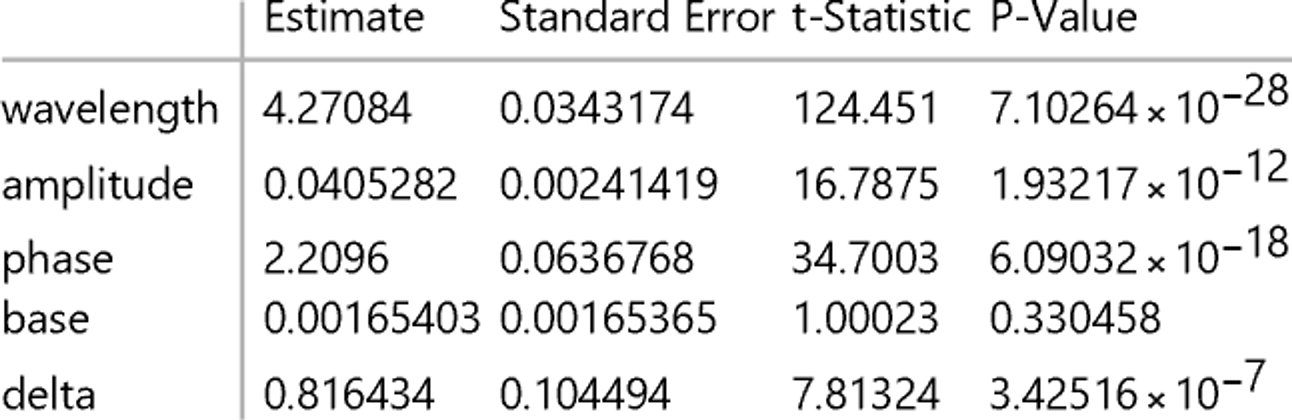
One can see that delta (the parameter characterizing the departure from a square wave) is highly significant (meaning it is significantly different from zero). While the underlying physical process might be a square wave, the measurement process does not result in a square wave and maybe a trapezoidal wave is a better approximation of the results from measurements.

You can compare all of models in the provided answers using nlm["AICc"]. This provides a relative ranking of the models from all of the answers here with the better models having smaller AICc values.

Maybe:

Hi Jim, I'll take the liberty of answering for Marius.

His very useful model is

a Tanh[r Sin[k (x - x0)]]+b

Assuming a and r are chosen not negative. By inspection, it is at a maxima when the Sin function is at +1, where it has a value of

b + a Tanh[r]

and a minima where the Sin function is at -1, where it has a value of

b - a Tanh[r]

Just for fun, I did this by the usual method of derivatives. I attach the notebook.

Attachments:

Max Min 1.nb

Given my previous comments, I wonder if your data was generated by a trapezoidal wave rather than a square wave.

data={{-6.25, 0.00219649}, {-5.75, 0.0291773}, {-5.25, 0.0428364}, {-4.75, 0.0418075}, 
  {-4.25, 0.0390189}, {-3.75, 0.0142977}, {-3.25, 0.000728449}, {-2.75, 0.000577218}, 
  {-2.25, 0.00314383}, {-1.75, 0.0275447}, {-1.25, 0.0428128}, {-0.75, 0.0433703}, 
  {-0.25, 0.0433703}, {0.25, 0.0403935}, {0.75, 0.0160277}, {1.25, 0.000686316}, 
  {1.75, 0.00036222}, {2.25, 0.00288114}, {2.75, 0.0256044}, {3.25, 0.0416728}, 
  {3.75, 0.0429419}, {4.25, 0.0396677}, {4.75, 0.0162309}};

nlm = NonlinearModelFit[data,
   (a/\[Pi])*(ArcSin[Sin[(\[Pi]/m) x + l]] + ArcCos[Cos[(\[Pi]/m) x + l]]) - a/2 + c,
   {{a, 0.04}, {m, 2}, {l, 3}, {c, 0.02}}, x];
Show[ListPlot[data], Plot[nlm[x], {x, Min[data[[All, 1]]], Max[data[[All, 1]]]}]]

The equation was lifted from Amrtanshu Raj 's answer at https://uk.mathworks.com/matlabcentral/answers/684163-generating-periodic-trapezoidal-waves-with-ramps. (Yes, a MATLAB site.)

I believe you that the "maxima show rolloff effects." But what does that mean? I don't speak that language. Might there be a need to include that "effect" in the modeling?

Hi James, The parameter a being negative is only a phase inversion, which would be compensated in the fit by a different value of x0. It can be forced positive by including a condition in the model like this:

sinFit = 
 NonlinearModelFit[LPGdata, {sineWave[x, a, x0, b], a > 0}, {a, x0, b},
   x]

I am also disappointed that the peaks are modeled poorly in the square wave fit. It is likely due to the midlevel values in the data. Stripping these out before the fit could improve the result. But data manipulation carries its own risks.

Hi Jamesa, The attached notebook takes a perhaps too naïve approach. It does select data to be processed. It estimates the peaks using data with y values greater then 80% of the max, and the valleys using values less than 20% of the max.

Attachments:

MinMax by Data R...nb

Thanks for your input, Anton. I appreciate your help. Did this actually use x0 as a fit parameter? It look like it just set the value to 1.000... with 0 uncertainty.