In continuation of the study here: https://community.wolfram.com/groups/-/m/t/1433064

Here we give three tests for the problem of natural convection of air in a rectangular cavity with a Rayleigh number of $Ra=10^4$ and with the time-fractional derivative $\partial_t^{\alpha}$ in the Caputo sense. On the side walls of the cavity a constant temperature difference is maintained, the upper and lower walls are thermally insulated. We use the Boussinesq approximation. As a benchmark solution, we use the data from the article:

Vahl Davis, G.de (1983) : Natural convection of air in a square cavity : A bench mark numerical solution. Int. J. Numer. Methods Fluids 3, 249-264.

Coincidence in all three tests is generally good. Thus, we showed the application of the method for solving the problems of thermal convection in the case of laminar flows. In a case of ordinary derivative $\partial_t$ this problem has been considered with using the Mathematica FEM on our page here. The code below is an implementation the finite difference method. We used fractional time step approximation of order $2-\alpha, 3-\alpha, 4-\alpha$ proposed by

R. Mokhtari and F. Mostajeran. A high order formula to approximate the Caputo fractional derivative. Commun. Appl. Math. Comput. 2, 1–29, 2019.

This algorithm has been tested in our papers

Zafar Hayat Khan, Oluwole Daniel Makinde, Alexander Trounev, Waqar Ahmed Khan, and Rashid Ahmad. Entropy generation and heat transfer in time-fractional mixed convection of nanofluids in Darcy-Forchheimer porous channel. Engineering Science and Technology, an International Journal, 60:101908,2024. https://doi.org/10.1016/j.jestch.2024.101908

Zafar Hayat Khan, Meijiang Zhou, Alexander Trounev, and Waqar Ahmed Khan. Modeling liquid–vapor fronts in porous media using time-fractional derivatives: An innovative framework. Physics of Fluids,37(3):032112, 03 2025. https://doi.org/10.1063/5.0259241

Code 1.

XYgrid[dom_List, pts_List] := 
  MapThread[
   N@Range[Sequence @@ #1, Abs[Subtract @@ #1]/#2] &, {dom, pts - 1}];
BoundaryIndex[xgridlen_, ygridlen_] := 
  Module[{tmp, left, right, bot, top, left1, right1}, 
   tmp = Table[(n - 1) ygridlen + Range[1, ygridlen], {n, 1, 
      xgridlen}]; {left, right} = tmp[[{1, -1}]]; {left1, right1} = 
    tmp[[{2, -2}]]; {bot, top} = 
    Transpose[{First[#], Last[#]} & /@ tmp]; {top, right[[2 ;; -2]], 
    bot, left[[2 ;; -2]], right1[[2 ;; -2]], left1[[2 ;; -2]]}];
Attributes[MakeVariables] = {Listable};
MakeVariables[var_, n_] := Table[Unique[var], {n}];
FDMat[deriv_, xygrid_, difforder_] := 
 Map[NDSolve`FiniteDifferenceDerivative[#, xygrid, 
     "DifferenceOrder" -> difforder]["DifferentiationMatrix"] &, deriv]
{dt, tmax, domain, pts, difforder, Ra, Pr, q} = {1/100, 
   100, {{0, 1}, {0, 1}}, {31, 31}, 4, 10^4, .7, 9/10};
xygrid = XYgrid[domain, pts]; {nx, ny} = 
 Map[Length, xygrid]; {top, right, bot, left, right1, left1} = 
 BoundaryIndex[nx, ny]; {dx, dy, dx2, dy2} = 
 FDMat[{{1, 0}, {0, 1}, {2, 0}, {0, 2}}, xygrid, difforder]; {dx1, 
  dy1} = FDMat[{{1, 0}, {0, 1}}, xygrid, 1]; {uvar0, vvar0, tvar0, 
  pvar0} = Table[ConstantArray[0, {nx ny, tmax}], {4}]; boundaries = 
 Join[top, right, bot, left]; sgrid = 
 Flatten[Outer[List, Sequence @@ xygrid], 1]; {uvar1, vvar1, tvar1, 
  pvar1} = MakeVariables[{uu, vv, tt, pp}, nx ny];


(*Caputo numerical derivative with order of accuracy 3-\[Alpha],4-\
\[Alpha]*)
a[j_][q_] := (j + 1)^(1 - q) - j^(1 - q); \[Beta][j_][
  q_] := -(1/6 ((j + 1)^(1 - q) + 2 j^(1 - q)) + 
    j^(2 - q)/(2 - q) - ((j + 1)^(3 - q) - j^(3 - q))/((2 - q) (3 - q)));
b[j_][q_] := ((j + 1)^(2 - q) - j^(2 - q))/(2 - 
      q) - ((j + 1)^(1 - q) + j^(1 - q))/2;

(*Caputo numerical derivative with order of accuracy 2-\[Alpha]*)
cj = Table[(j + 1)^(1 - q) - j^(1 - q), {j, tmax + 1}];

(*Fractional pde numerical solution 3-alpha*)

time = AbsoluteTiming[
   Do[{uvar, vvar, tvar, pvar} = {uvar0[[All, i]], vvar0[[All, i]], 
      tvar0[[All, i]], pvar[[All, i]]}; n = i + 1; 
    c[0] = If[n == 1, 1, a[0][q] + b[0][q]]; 
    Do[c[j] = a[j][q] + b[j][q] - b[j - 1][q];, {j, 1, n - 2}]; 
    c[n - 1] = a[n - 1][q] - b[n - 2][q]; 
    cdt = dt^(-q)/
       Gamma[2 - q] (c[0] tvar1 - c[n - 1] tvar0[[All, 1]] - 
        Sum[(c[n - j - 1] - c[n - j]) tvar0[[All, j]], {j, 1, n - 1}]);
     cdu = dt^(-q)/
       Gamma[2 - q] (c[0] uvar1 - c[n - 1] uvar0[[All, 1]] - 
        Sum[(c[n - j - 1] - c[n - j]) uvar0[[All, j]], {j, 1, n - 1}]);
     cdv = dt^(-q)/
       Gamma[2 - q] (c[0] vvar1 - c[n - 1] vvar0[[All, 1]] - 
        Sum[(c[n - j - 1] - c[n - j]) vvar0[[All, j]], {j, 1, n - 1}]);
     eqnu = cdu + uvar (dx . uvar1) + vvar (dy . uvar1) - 
      Pr (dx2 + dy2) . uvar1 + dx . pvar1; 
    eqnv = cdv + uvar (dx . vvar1) + vvar (dy . vvar1) - Ra Pr tvar1 -
       Pr (dx2 + dy2) . vvar1 + dy . pvar1;
    eqnt = 
     cdt + uvar (dx . tvar1) + vvar (dy . tvar1) - (dx2 + dy2) . tvar1;
    eqnp = dx . uvar1 + dy . vvar1;
    eqnu[[boundaries]] = uvar1[[boundaries]]; 
    eqnv[[boundaries]] = vvar1[[boundaries]]; 
    eqnt[[left]] = tvar1[[left]] - 1; eqnt[[right]] = tvar1[[right]]; 
    eqnt[[bot]] = (dy . tvar1)[[bot]]; 
    eqnt[[top]] = (dy . tvar1)[[top]]; 
    eqnp[[right]] = (dx . pvar1)[[right]]; 
    eqnp[[left]] = (dx . pvar1)[[left]]; 
    eqnp[[top]] = (dy . pvar1)[[top]]; 
    eqnp[[bot]] = (dy . pvar1)[[bot]]; 
    eqn = Join[eqnu, eqnv, eqnt, eqnp]; 
    var = Join[uvar1, vvar1, tvar1, pvar1]; {vec, mat} = 
     CoefficientArrays[eqn, var]; 
    sol = LinearSolve[mat, -vec]; {uvar0[[All, i + 1]], 
      vvar0[[All, i + 1]], tvar0[[All, i + 1]], pvar0[[All, i + 1]]} =
      Partition[sol, Length[sgrid]]; 
    Nu = Mean[-(dx . tvar0[[All, i + 1]])[[left]]];, {i, 1, 
     tmax - 1}]; {Max[Abs[uvar0[[All, -1]]]], Max[Abs[vvar0[[All, -1]]]],
     Nu}];

How to use

time
Out[]= {225.626,{16.2676,19.5971,2.28378}}
mem=MemoryInUse[]
Out[]= 148360240  

Code 2

(*Fractional pde numerical solution 2-alpha*)


time1 = AbsoluteTiming[
   Do[{uvar, vvar, tvar, pvar} = {uvar0[[All, i]], vvar0[[All, i]], 
      tvar0[[All, i]], pvar[[All, i]]}; 
    cdt = dt^(-q)/
       Gamma[2 - q] (tvar1 - tvar + 
        Sum[cj[[j]] (tvar0[[All, i - j + 1]] - 
            tvar0[[All, i - j]]), {j, 1, i - 1}]); 
    cdu = dt^(-q)/
       Gamma[2 - q] (uvar1 - uvar + 
        Sum[cj[[j]] (uvar0[[All, i - j + 1]] - 
            uvar0[[All, i - j]]), {j, 1, i - 1}]); 
    cdv = dt^(-q)/
       Gamma[2 - q] (vvar1 - vvar + 
        Sum[cj[[j]] (vvar0[[All, i - j + 1]] - 
            vvar0[[All, i - j]]), {j, 1, i - 1}]); 
    eqnu = cdu + uvar (dx . uvar1) + vvar (dy . uvar1) - 
      Pr (dx2 + dy2) . uvar1 + dx . pvar1; 
    eqnv = cdv + uvar (dx . vvar1) + vvar (dy . vvar1) - Ra Pr tvar1 -
       Pr (dx2 + dy2) . vvar1 + dy . pvar1;
    eqnt = 
     cdt + uvar (dx . tvar1) + vvar (dy . tvar1) - (dx2 + dy2) . tvar1;
    eqnp = dx . uvar1 + dy . vvar1;
    eqnu[[boundaries]] = uvar1[[boundaries]]; 
    eqnv[[boundaries]] = vvar1[[boundaries]]; 
    eqnt[[left]] = tvar1[[left]] - 1; eqnt[[right]] = tvar1[[right]]; 
    eqnt[[bot]] = (dy . tvar1)[[bot]]; 
    eqnt[[top]] = (dy . tvar1)[[top]]; 
    eqnp[[right]] = (dx . pvar1)[[right]]; 
    eqnp[[left]] = (dx . pvar1)[[left]]; 
    eqnp[[top]] = (dy . pvar1)[[top]]; 
    eqnp[[bot]] = (dy . pvar1)[[bot]]; 
    eqn = Join[eqnu, eqnv, eqnt, eqnp]; 
    var = Join[uvar1, vvar1, tvar1, pvar1]; {vec, mat} = 
     CoefficientArrays[eqn, var]; 
    sol = LinearSolve[mat, -vec]; {uvar0[[All, i + 1]], 
      vvar0[[All, i + 1]], tvar0[[All, i + 1]], pvar0[[All, i + 1]]} =
      Partition[sol, Length[sgrid]]; 
    Nu = Mean[-(dx . tvar0[[All, i + 1]])[[left]]];, {i, 1, 
     tmax - 1}]; {Max[Abs[uvar0[[All, -1]]]], Max[Abs[vvar0[[All, -1]]]],
     Nu}];

 time1

Out[]= {53.5124, {16.2677, 19.5972, 2.2838}}

 mem1 = MemoryInUse[]

Out[]= 160745544

Code 3.

(*Fractional pde numerical solution 4-alpha*)


time2 = AbsoluteTiming[
   Do[{uvar, vvar, tvar, pvar} = {uvar0[[All, i]], vvar0[[All, i]], 
      tvar0[[All, i]], pvar[[All, i]]}; n = i + 1; 
    c[0] = If[n == 1, 1, 
      If[n == 2, a[0][q] + b[0][q], a[0][q] + b[0][q] + \[Beta][0][q]]];
     c[1] = If[n == 2, a[2][q] - b[1][q], 
      If[n == 3, a[1][q] + b[1][q] - b[0][q] - 2 \[Beta][0][q], 
       a[1][q] + b[1][q] - b[0][q] + \[Beta][3][q] - 2 \[Beta][0][q]]];
     c[2] = If[n == 3, a[2][q] - b[1][q] + \[Beta][0][q], 
      a[2][q] + b[2][q] - b[1][q] + \[Beta][4][q] - 
       2 \[Beta][5][q] + \[Beta][0][q]]; 
    If[n >= 4, 
     Do[c[j] = 
        a[j][q] + b[j][q] - b[j - 1][q] + \[Beta][j][q] - 
         2 \[Beta][j - 1][q] + \[Beta][j - 2][q];, {j, 3, n - 3}]; 
     c[n - 2] = 
      a[n - 2][q] + b[n - 2][q] - b[n - 3][q] + \[Beta][n - 4][q] - 
       2 \[Beta][n - 3][q]; 
     c[n - 1] = a[n - 1][q] - b[n - 2][q] + \[Beta][n - 3][q]]; 
    cdt = dt^(-q)/
       Gamma[2 - q] (c[0] tvar1 - c[n - 1] tvar0[[All, 1]] - 
        Sum[(c[n - j - 1] - c[n - j]) tvar0[[All, j]], {j, 1, n - 1}]);
     cdu = dt^(-q)/
       Gamma[2 - q] (c[0] uvar1 - c[n - 1] uvar0[[All, 1]] - 
        Sum[(c[n - j - 1] - c[n - j]) uvar0[[All, j]], {j, 1, n - 1}]);
     cdv = dt^(-q)/
       Gamma[2 - q] (c[0] vvar1 - c[n - 1] vvar0[[All, 1]] - 
        Sum[(c[n - j - 1] - c[n - j]) vvar0[[All, j]], {j, 1, n - 1}]);
     eqnu = cdu + uvar (dx . uvar1) + vvar (dy . uvar1) - 
      Pr (dx2 + dy2) . uvar1 + dx . pvar1; 
    eqnv = cdv + uvar (dx . vvar1) + vvar (dy . vvar1) - Ra Pr tvar1 -
       Pr (dx2 + dy2) . vvar1 + dy . pvar1;
    eqnt = 
     cdt + uvar (dx . tvar1) + vvar (dy . tvar1) - (dx2 + dy2) . tvar1;
    eqnp = dx . uvar1 + dy . vvar1;
    eqnu[[boundaries]] = uvar1[[boundaries]]; 
    eqnv[[boundaries]] = vvar1[[boundaries]]; 
    eqnt[[left]] = tvar1[[left]] - 1; eqnt[[right]] = tvar1[[right]]; 
    eqnt[[bot]] = (dy . tvar1)[[bot]]; 
    eqnt[[top]] = (dy . tvar1)[[top]]; 
    eqnp[[right]] = (dx . pvar1)[[right]]; 
    eqnp[[left]] = (dx . pvar1)[[left]]; 
    eqnp[[top]] = (dy . pvar1)[[top]]; 
    eqnp[[bot]] = (dy . pvar1)[[bot]]; 
    eqn = Join[eqnu, eqnv, eqnt, eqnp]; 
    var = Join[uvar1, vvar1, tvar1, pvar1]; {vec, mat} = 
     CoefficientArrays[eqn, var]; 
    sol = LinearSolve[mat, -vec]; {uvar0[[All, i + 1]], 
      vvar0[[All, i + 1]], tvar0[[All, i + 1]], pvar0[[All, i + 1]]} =
      Partition[sol, Length[sgrid]]; 
    Nu = Mean[-(dx . tvar0[[All, i + 1]])[[left]]];, {i, 1, 
     tmax - 1}]; {Max[Abs[uvar0[[All, -1]]]], Max[Abs[vvar0[[All, -1]]]],
     Nu}];

 time2

Out[]= {648.823, {16.2676, 19.597, 2.28373}}

 mem2 = MemoryInUse[]

Out[]= 161635008

Cumulative table looks like

TableForm[{{2 - \[Alpha], time1[[1]], mem1, time1[[2, 1]], 
   time1[[2, 2]], time1[[2, 3]]}, {3 - \[Alpha], time[[1]], mem, 
   time[[2, 1]], time[[2, 2]], time[[2, 3]]}, {4 - \[Alpha], time2[[1]],
    mem2, time2[[2, 1]], time2[[2, 2]], time2[[2, 3]]}}, 
 TableHeadings -> {None, {"Order", "Time", "Memory", "Max|u|" , 
    "Max|v|", "\!\(\*SubscriptBox[\(Nu\), \(mean\)]\)"}}]

The results computed on 2 different machines Intel Pentium Silver "Lenovo" and "Dell" with Mathematica 14.2.1 for Microsoft Windows (64-bit) (March 17, 2025) are shown below 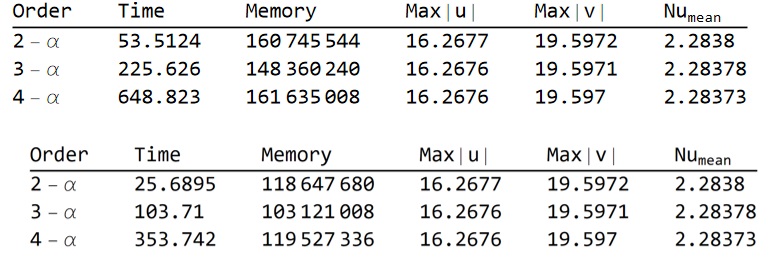Note, the benchmark solution for this problem is Max|u|=16.178, Max|v|=19.617, $Nu_{mean}=2.243$. We used above the grid $31\times 31$, while for benchmark solution they used several grids and extrapolation.