Here's a representation of how I show my students. It's for strictly composite formulas, by which I mean functions of the form
$f\circ g \circ \cdots \circ h$ or as a formula
$f(g(\cdots h(x)))$. It won't deal with a formula like the following:
$$f\left(g\bigl(h(k(l(x)))\cdot m(n(x)+p(q(r(x))))\bigr)\right) \tag{1}$$
The extreme elaborateness of
$(1)$ is just to drive home why I wouldn't consider going "inside-out" with the chain rule. I suppose it's clear enough what to do on
$\ln(\cos(e^x))$, but when the inside components involve combinations of sums, products, quotients, and compositions such as
$\ln(\cos(x^2)+\sin(e^{3x})$, where do you start on the inside? At
$x^2$ or
$3x$? Or do you start in the middle with
$\cos(x^2)+\sin(e^{3x}$ and work your way both up and down? How in the world could I ever explain the process to a group of students?
But mainly I go "outside-in", because that's how I was taught and that's all I have ever done. My first year in college in 1981, I was introduced to computational symbolic algebra in first-year math (via LISP). A couple of years later, I learned to write parsers, and I wrote a small CAS for fun. Programming the chain rule seemed natural to go outside-in. Yet another reason is that when you start substitution in integrals, the first examples generally involve substitutions where one lets
$u$ be the inside of the outermost function of one the factors. Thus outside-in is a way to quickly identify probable substitutions. If one goes inside-out, several consecutive substitutions might be needed.
Finally, one calculus book I once used wrote the chain rule in a hybrid Leibniz way,
$d(f(u)) = f'(u) \; du$, and the derivative rules for all the particular functions in the corresponding differential form like this:
$d(\cos u)=(-\sin u) \; du$, etc. At the end of the process, you divide by
$dx$ or whatever to get the derivative. It was meant to be used outside-in as follows:
$${
d(\ln(\cos e^x))
={1\over \cos e^x}\cdot d(\cos e^x)
={1\over \cos e^x}(-\sin e^x) \cdot d(e^x)
={-\sin e^x\over \cos e^x} e^x \;dx
}$$
Then divide by
$dx$.
In any case, I usually teach it outside-in with the derivative operator
$d/dx$ instead of the differential operator as follows:
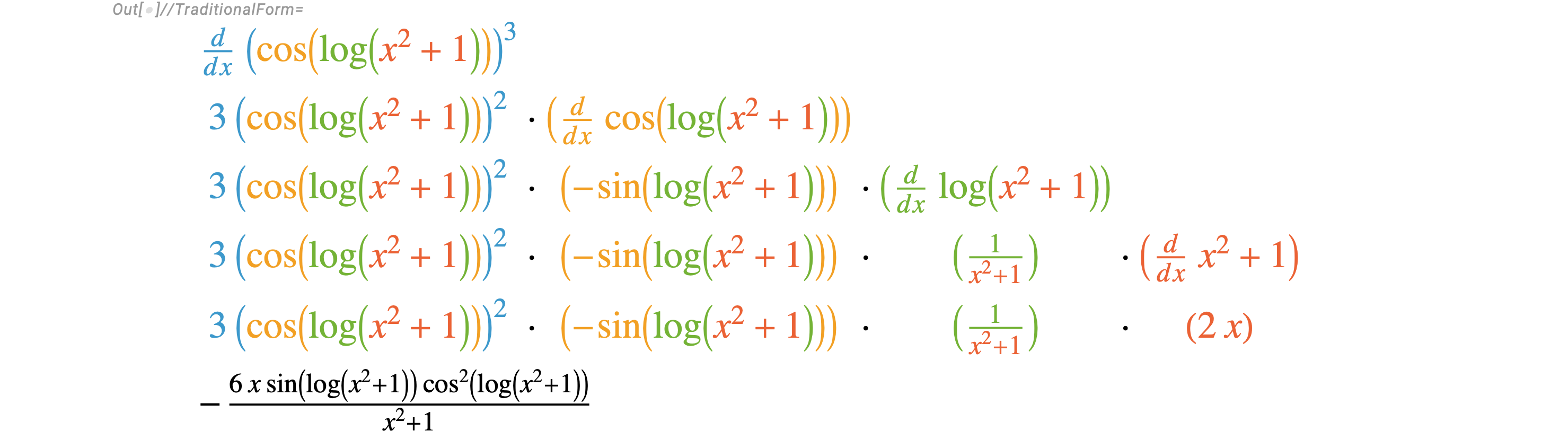
Of course, I don't write such colors on the board in class. (I usually underline the inside part to be differentiated on the outside per the chain rule, as a way to highlight it.)
Code dump
Fancy formatting needs fancy code unfortunately.
ClearAll[dt, dd, pow, exp, pp];
(* Univariate forms of Power[] *)
pow[k_]'[x_] :=
If[k == 2, 2 x, k*pow[k - 1][x]]; (* power functions #^k& *)
exp[k_]'[x_] := Log[k]*exp[k][x]; (* exponential functions k^#& *)
toUnivariatePower = {sum_Plus :> sum, term_Times :> term,
Power[a_, b_] /; ! FreeQ[a, x] :> pow[b][a],
Power[a_, b_] /; ! FreeQ[b, x] :> exp[a][b]};
fromUnivariatePower = {pow[b_][a_] :> Power[a, b],
exp[a_][b_] :> Power[a, b]};
MakeBoxes[pow[k_][x_], form_] :=
SuperscriptBox[RowBox[{"(", MakeBoxes[x, form], ")"}],
MakeBoxes[k, form]];
MakeBoxes[exp[k_][x_], form_] := MakeBoxes[Power[k, x], form];
(* Extra parentheses and the derivative operator (for output display) *)
MakeBoxes[pp[y : _. pow[_][_]], form_] :=(* don't parenthesize *)
MakeBoxes[y, form];
MakeBoxes[pp[y_], form_] :=(* parenthesize *)
RowBox[{"(", MakeBoxes[y, form], ")"}];
MakeBoxes[dd[y_], form_] :=(* derivative operator *)
RowBox[{ (* choose "d" or "\[PartialD]" *)
FractionBox["d", "d\[InvisibleSpace]x"],
MakeBoxes[y, form]}];
dt[f_[x_], "Style", n_] :=
Style[f[dt[x, "Style", n + 1]], ColorData[116][n]];
dt[y_, "Style", n_] := Style[y, ColorData[116][n]];
dt[y_] := TraditionalForm@Grid[
Replace[
Rest /@ dt[dt[murf = y //. toUnivariatePower, "Style", 1], {}]
, row_List /; Length@row > 1 && FreeQ[row, SpanFromLeft] :>
Replace[row, Style[x_, s_] :> Style[pp@x, s], 1], 1]
, Alignment -> Automatic, Spacings -> {0, Automatic}];
dt[sf : Style[f_[x_], s__],
pre_] := {{Sequence @@ pre, " \[CenterDot] ", Style[dd[f[x]], s]},
Sequence @@ dt[x, Join[pre, {" \[CenterDot] ", Style[f'[x], s]}]]};
dt[sy : Style[y_, s__],
pre_] := {{Sequence @@ pre, " \[CenterDot] ", Style[dd[y], s]},
Sequence @@ dt[x, Join[pre, {"\[CenterDot]", Style[D[y, x], s]}]]};
dt[x, pre_] := {pre, {Null,
Item[Times @@ pre[[2 ;; ;; 2]] /.
RawBoxes -> (ReleaseHold@
MakeExpression[#, TraditionalForm] &) /.
Style -> (# &) //. fromUnivariatePower, Alignment -> Left],
SpanFromLeft}};
(* Example shown above: *)
dt[Cos[Log[x^2 + 1]]^3]