Dear Farah,
I understand that it can be confusing at first to solve all these different problems, using slightly different functions/commands. As Udo Krause suggested you could use Reduce for this second problem. You can also use Solve:
Solve[Sin[x]^2 - Cos[x]^2 == 1, x]
This gives the result in radian, but it can be easily converted to Degree using another command in the Wolfram Language:
Needs["Units`"]
Solve[Sin[x]^2 - Cos[x]^2 == 1, x]
Convert[Evaluate[x /. %[[1]]], Degree]
It might look a bit intimidating at first, but it is actually quite simple. These commands build up, i.e. you nest them and the expressions become larger and to the untrained eye difficult to decipher.
You ask whether you should rather use learn the Wolfram Language. I personally would strongly suggest to learn it. It is much more flexible than just using WolframAlpha, which is of course a powerful tool, too. If you learn the Wolfram Language you will soon be able to "ask" complicated questions and you will have a fantastic tool to support your learning of Mathematics. I don't think that knowing how to use Mathematica can substitute learning and understanding mathematics, but it certainly can support your learning a great deal. You can check results of problems you solved or sometimes even get step-by-step solutions. But you can do so much more. Very often when you learn mathematics the problems in textbooks are rather dull and it feels like a chore to have to solve them. Often that is because the really interesting problems are much too complicated to solve with paper and pencil - some very advanced mathematicians might be able to do that at least partially, but at School or even as an Undergraduate student at University you might not be able to do it. Mathematica is what you need to extend what you have learnt at School to really interesting problems. If you learn the Wolfram Language you might actually find that, after a little training, you can solve your maths problems, but also that maths can be fun. You can get a much deeper understanding of what is going on if you use mathematica to "figure stuff out". For example your first question, treats an identity to "split" a sine function into a sum of products of sine and cosine functions. Have a look at this demonstration project:
http://demonstrations.wolfram.com/AdditionFormulaForSine/
The key output looks like this:
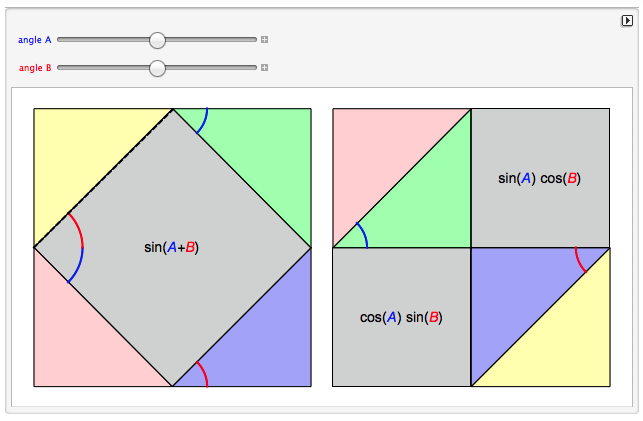
By just rearranging the coloured triangles you can actually see why the result that Mathematica gives is true. Actually, if you understand that figure you can easily write down the mathematical proof, why this is true.
It is definitely worthwhile to learn Mathematica. You will still have to learn the maths, but it will be more fun.
Cheers,
Marco
PS: Here you can find some other examples of what Mathematica can do with trigonometric identities.