a) I do not know what you mean by "develop" here.

b) sin(x+55°) is simpler than sin x cos(55°) + cos(x) sin(55°).

c) Is the result that Wolfram|Alpha gives you actually wrong, or just different? It gives me cos((7 pi)/36-x), which appears to be equivalent.

In[1]:= FullSimplify[ Cos[(7 Pi)/36 - x] -  Sin [x + 55 \[Degree]],  Element[x, Reals]] 
Out[1]= 0 

Can you show us the output you get, either with a screen shot, or by clicking on it, then clicking the A in the little menu that pops down, then copying the text version?

Thanks for the answer, but how should i know the next time if i have a problem? must i learn the wolframalpha langue that you suggested?

I tested with a new question sin^2(x)- cos^2(x) =1 in the book it says the answer are x = 90°+ n x 360° . How should i think here? Iam really sorry if iam bothering you.

Generally, the problems you are discussing involve working with trig identities. These are part of the core learning in a trigonometry class. They are most useful when manipulating trig expressions into a form which, for some reason, makes the underlying structure of the model more evident. Most often, this is something being done (please forgive me) with pencil and paper. The reason for this is that, while Mathematica is a marvelous tool, all such tools still fall far short of the capabilities of the human mind.

I would guess that one reason for that lies in the words "more evident." In working physics problems, for example, those who have done it for a long time (and some right away) develop an intuition that tells them when a particular rearrangement of an expression is moving toward a more useful form. They know they are trying to get to a form which will make certain characteristics of the model evident. An example might be the derivation of a wave equation from Maxwell's equations. He knew immediately that what he had was astounding.

Hi Udo, Wittgenstein is my favorite philosopher! And I think very apropos to this discussion. He called philosophy "thinking befuddled by language," and told us that the most difficult answers to find were the answers to invalid or ill-defined questions. By eliminating such questions, he came to the conclusion that he had solved all the real questions in philosophy, and was amazed at how little he had done.

In the very first post, Farah says, "The question is: simplify and develop sin (x+55°)." To ask anyone or any tool to answer that requires a clear definition. Bruce points out that sin(a+b) is simpler than sin(a)cos(b)+cos(a)sin(b). That is certainly true by the most obvious criteria, but probably not what the trig teacher had in mind. I suspect that a better statement of the intended problem would be, "find an equivalent expression in which all arguments appear as atomic forms." Perhaps there is a way to tell Mathematica that in its repeated evaluations that would be a simpler and irreducible form.

Best, David

Dear Farah,

I understand that it can be confusing at first to solve all these different problems, using slightly different functions/commands. As Udo Krause suggested you could use Reduce for this second problem. You can also use Solve:

Solve[Sin[x]^2 - Cos[x]^2 == 1, x]

This gives the result in radian, but it can be easily converted to Degree using another command in the Wolfram Language:

Needs["Units`"]
Solve[Sin[x]^2 - Cos[x]^2 == 1, x]
Convert[Evaluate[x /. %[[1]]], Degree]

It might look a bit intimidating at first, but it is actually quite simple. These commands build up, i.e. you nest them and the expressions become larger and to the untrained eye difficult to decipher.

You ask whether you should rather use learn the Wolfram Language. I personally would strongly suggest to learn it. It is much more flexible than just using WolframAlpha, which is of course a powerful tool, too. If you learn the Wolfram Language you will soon be able to "ask" complicated questions and you will have a fantastic tool to support your learning of Mathematics. I don't think that knowing how to use Mathematica can substitute learning and understanding mathematics, but it certainly can support your learning a great deal. You can check results of problems you solved or sometimes even get step-by-step solutions. But you can do so much more. Very often when you learn mathematics the problems in textbooks are rather dull and it feels like a chore to have to solve them. Often that is because the really interesting problems are much too complicated to solve with paper and pencil - some very advanced mathematicians might be able to do that at least partially, but at School or even as an Undergraduate student at University you might not be able to do it. Mathematica is what you need to extend what you have learnt at School to really interesting problems. If you learn the Wolfram Language you might actually find that, after a little training, you can solve your maths problems, but also that maths can be fun. You can get a much deeper understanding of what is going on if you use mathematica to "figure stuff out". For example your first question, treats an identity to "split" a sine function into a sum of products of sine and cosine functions. Have a look at this demonstration project:

http://demonstrations.wolfram.com/AdditionFormulaForSine/

The key output looks like this:

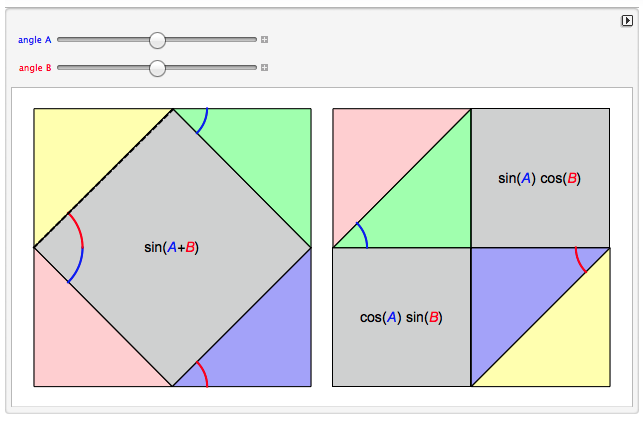
By just rearranging the coloured triangles you can actually see why the result that Mathematica gives is true. Actually, if you understand that figure you can easily write down the mathematical proof, why this is true.

It is definitely worthwhile to learn Mathematica. You will still have to learn the maths, but it will be more fun.

Cheers,

Marco

PS: Here you can find some other examples of what Mathematica can do with trigonometric identities.