Hi David,
I am not sure whether I fully understand your question, but this might help. First we can plot the curves>
ContourPlot[{2 y^2 == x + 4, x == y^2}, {x, -4, 10}, {y, -4, 4}]
which gives
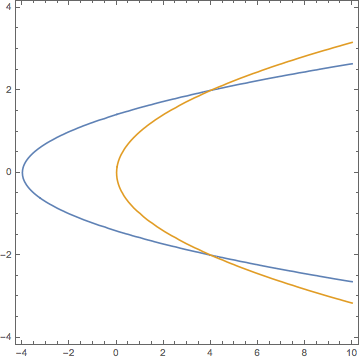
Now you see that the area between the curves will be infinite, because there is a difference of the curves right of the intersection points. For the next calculation I assume that you want the area of the finite bit for
$-4<x<4$. In that case you could try
Integrate[2*Sqrt[(x + 4)/2], {x, -4, 0}] + Integrate[2*(Sqrt[(x + 4)/2] - Sqrt[x]), {x, 0, 4}]
Which gives, after using Simplify, 32/3. Alternatively, this should work
Integrate[x^2 - (2 x^2 - 4), {x, -2, 2}]
Luckily, it gives the same result.
Cheers,
Marco