Hi Amy,

This is not their code, but may be a little easier to see into. It defines a function for the potential generated by a single charge, sums this for a list of charges, and then uses E = - grad V to get the field.

(* set the directory so we export plots it *)
SetDirectory[NotebookDirectory[]];

(* define a vector norm that does not use Abs *)
norm[a_] := Sqrt[a.a]

(* the potential at point (x,y) generated by charge q at (px,py) *)
ePot[{x_, y_}, {px_, py_, q_}] := q/norm[{x, y} - {px, py}]

(* the potential of a point charge at the origin *)
p1 = Plot3D[ePot[{x, y}, {0, 0, 1}], {x, -2, 2}, {y, -2, 2}]

(* a list of charges *)
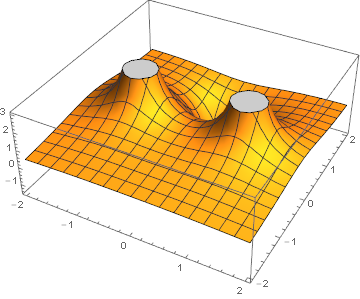
charges = {{-1, 0, 1}, {1, 0, 1}, {0, 1, -1}};

(* total potential at (x,y) from all the charges in a list *)
totPot = Total[ePot[{x, y}, #] & /@ charges];

(* the total potential *)
p2 = Plot3D[totPot, {x, -2, 2}, {y, -2, 2}]

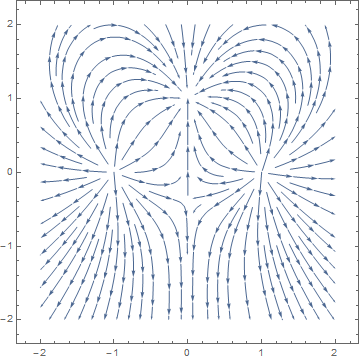
(* the field is minus the gradient of the potential *)
totField = -Grad[totPot, {x, y}];
p3 = StreamPlot[totField, {x, -2, 2}, {y, -2, 2}]