I believe it is because Plot first evaluates its argument.

What if I have something like this and I want to remove the asymptotes:

y = {-1,0,1}
Plot[A[x,y]/B[x,y],{x,0,1}]

Sould I use Exclusions->{B[x,y]!=0} or DeleteCases[B[x,y],0] or something else?

For every value of y, I have a different curve with an asymptote, so I must add an exclusion {B[x,-1]==0,B[x,0] == 0,B[x,1]==1} but the value of x in each exclusion will make a discontinuity on the other 2 curves also , then now I got rid of the asymptotes but as a result I will have 3 curves that each one of them contains two white spots inside of them. Do you agree ?

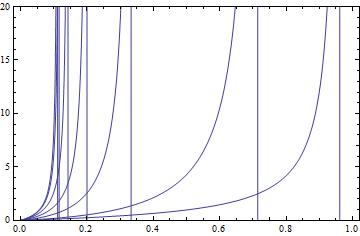
I want to plot the following 7 curves without their asymptotes:

\[Gamma] = {-0.99, -0.9, -0.5, 0, 0.5, 0.9, 0.99}

f[\[Lambda]_, \[Gamma]_] := (1 - 5 \[Lambda] + 4 \[Gamma]*\[Lambda]) (
  77 \[Lambda]^2 - 
   76 \[Gamma] \[Lambda]^2 + (10 \[Lambda] - 
      8 \[Gamma] \[Lambda]) (1 - 5 \[Lambda] + 
      4 \[Gamma] \[Lambda]))/(
  2 - (10 \[Lambda] - 8 \[Gamma] \[Lambda]) (2 - 5 \[Lambda] + 
      4 \[Gamma] \[Lambda]))

Plot[f[\[Lambda], \[Gamma]], {\[Lambda], 0, 1}, PlotRange -> {0, 20}, 
 Frame -> True]