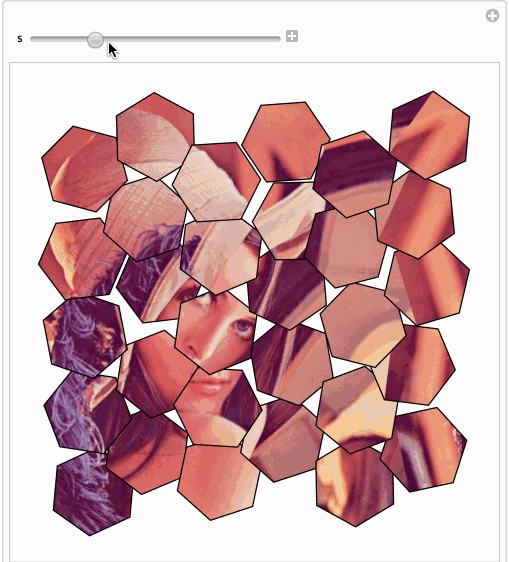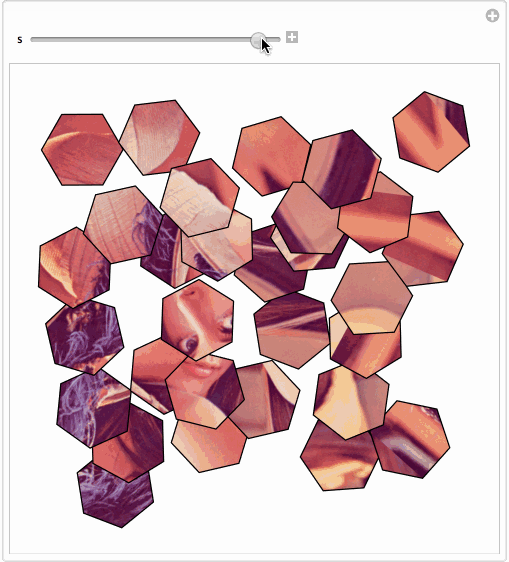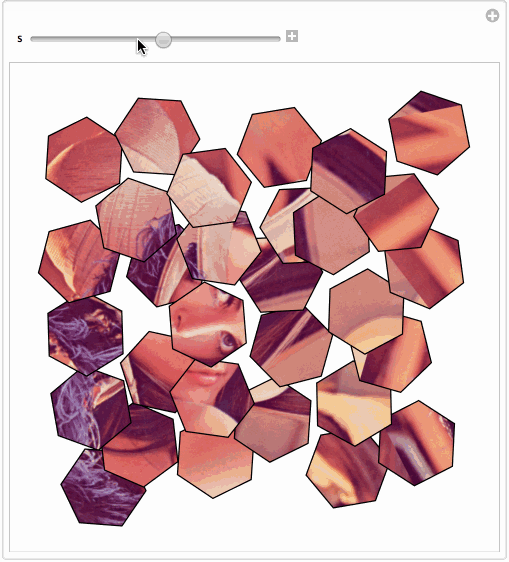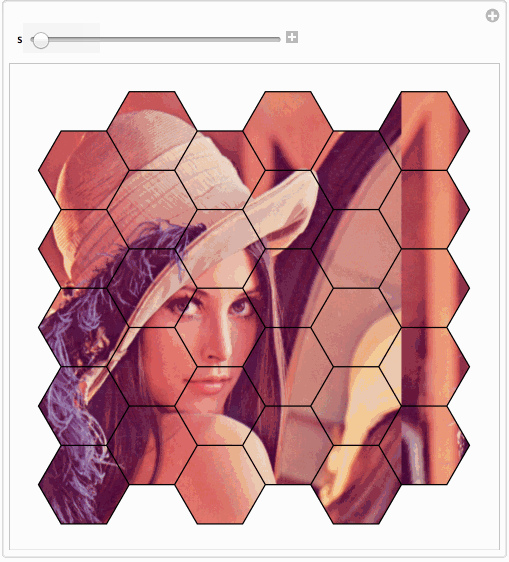
It is a bit not clear what you mean. Say you mean a simple overlap...

h[x_, y_] := Polygon[Table[.1 {Cos[2 Pi k/6] + x, Sin[2 Pi k/6] + y}, {k, 6}]]
hex = Graphics[{EdgeForm[Directive[Black, Thick]], FaceForm[], LightBlue, 
   Table[h[3 i + 3 ((-1)^j + 1)/4, Sqrt[3]/2 j], {i, 3}, {j, 10}]},  ImageSize -> 512]

ImageMultiply[{ExampleData[{"TestImage", "Lena"}], Rasterize@hex}]

Or maybe you'd like something (adopted from here ) fancier...

Manipulate[SeedRandom[1];
 Graphics[{EdgeForm[Black], Texture[ExampleData[{"TestImage", "Lena"}]], 
   GeometricTransformation[#, 
      Composition[TranslationTransform@RandomReal[.1 s {-1, 1}, 2], 
       RotationTransform[s RandomReal[{-Pi, Pi}], Mean@First[#]]]] & /@
     Cases[Normal@hex, 
     Polygon[p_, ___] :> Polygon[p, VertexTextureCoordinates -> p], Infinity]}], {s, 0, 1}]

I am not sure what "3, 4 or 5 levels" would look like - is there a link to a picture somewhere?

If one can build such a figure from polygons in Mathematica, then it is easy to use the same procedure - just this simple line will make texture mapping (partitioning):

Cases[ ..... , Polygon[p_, ___] :> Polygon[p, VertexTextureCoordinates -> p], Infinity]

no matter what complex arrangement of polygons we deal with.